Part 1. 数据结构

1.线段树（Segment Trees)

关键词：定长序列操作，区间修改与查询。

ACLibrary对懒标记线段树适配的定义，不涉及区间懒标记的普通线段树没有 $F$ 的限制：

It is the data structure for the pair of a monoid $(<S, \cdot>: S \cdot S \to S, e \in S)$ and a set $F$ of $S \to S$ mappings that satisfies the following properties.

$F$ contains the identity map $\mathrm{id}$ , where the identity map is the map that satisfies $\mathrm{id}(x) = x$ for all $x \in S$ .
$F$ is closed under composition, i.e., $f \circ g \in F$ holds for all $f, g \in F$ .
$f(x \cdot y) = f(x) \cdot f(y)$ holds for all $f \in F$ and $x, y \in S$ .

Given an array $S$ of length $N$ , it processes the following queries in $O(\log N)$ time.

Acting the map $f\in F$ (cf. $x = f(x)$ ) on all the elements of an interval
Calculating the product of the elements of an interval

中文翻译：

懒标记线段树是适配于满足以下条件的幺半群 $(<S, \cdot>: S \cdot S \to S, e \in S)$ 和属于线性空间 $V:S\to S$ 的子空间 $F$ :

$F$ 有单位映射 $f\in F,s.t.\ \forall x\in S, f(x)=x$
代数系统 $<F,\circ>$ 封闭，其中 $\circ$ 表函数复合，不满足交换律，复合顺序从右到左，即 $(f\circ g)(x)=f(g(x))$
$F$ 必须是线性空间，即 $\forall f \in F,$ $\forall x, y \in S, $ $f(x \cdot y) = f(x) \cdot f(y)$ .

给定一个长度为 $N$ 的 $S$ 类型的数组，要求在 $O(log\ N)$ 的时间内完成以下类型操作：

对一个或者一段区间的值应用线性映射 $f$ ，并改为对应结果。

$\forall x_i\in S,\ i\in[l,r), \ x_i:=f(x_i)$
求一个或者一段区间的值对幺半群乘法（ $\cdot$ ）运算的结果。

$\large ans=\prod_{i=l}^r x_i \in S$

1.1 普通线段树（静态开点区间加，永久化懒标记，当心爆标记问题，码量小）

切记单点修改的if-else必须写全！！！

#include <bits/stdc++.h>
using namespace std;
#define int long long
struct node
{
    int sum;
    int lazy;
};
const int maxn = 2e5 + 9;
node tree[maxn << 2];
void update(int pos, int val, int rt, int cl, int cr)
{
    tree[rt].sum += val;
    if (cl == cr)
    {
        return;
    }
    int mid = (cl + cr) >> 1;
    if (pos <= mid)
        update(pos, val, rt << 1, cl, mid);
    else
        update(pos, val, rt << 1 | 1, mid + 1, cr);
    return;
}
void update(int l, int r, int val, int rt, int cl, int cr)
{
    tree[rt].sum += val * (min(r, cr) - max(l, cl) + 1);
    if (l <= cl && cr <= r)
    {
        tree[rt].lazy += val;
        return;
    }
    int mid = (cl + cr) >> 1;
    if (l <= mid)
        update(l, r, val, rt << 1, cl, mid);
    if (r > mid)
        update(l, r, val, rt << 1 | 1, mid + 1, cr);
}
int query(int l, int r, int rt, int cl, int cr)
{
    if (l <= cl && cr <= r)
    {
        return tree[rt].sum;
    }
    int res = 0;
    int mid = (cl + cr) >> 1;
    if (l <= mid)
        res += query(l, r, rt << 1, cl, mid);
    if (r > mid)
        res += query(l, r, rt << 1 | 1, mid + 1, cr);
    return res + tree[rt].lazy * (min(r, cr) - max(l, cl) + 1);
}
signed main()
{
    int n;
    cin >> n;
    int q;
    cin >> q;
    for (int i = 1; i <= n; i++)
    {
        int x;
        cin >> x;
        update(i, x, 1, 1, n);
    }
    while (q--)
    {
        int op;
        cin >> op;
        if (op == 1)
        {
            int l, r, d;
            cin >> l >> r >> d;
            update(l, r, d, 1, 1, n);
        }
        else
        {
            int l, r;
            cin >> l >> r;
            cout << query(l, r, 1, 1, n) << endl;
        }
    }
    return 0;
}

1.2 普通线段树(静态开点区间加，标记永久化)

#include <bits/stdc++.h>
using namespace std;
#define int long long
struct node
{
    int sum;
    int lazy;
};
const int maxn = 2e5 + 9;
node tree[maxn << 2];
int a[maxn];
void pushup(int rt)
{
    tree[rt].sum = tree[rt << 1].sum + tree[rt << 1 | 1].sum;
    return;
}
void pushdown(int rt, int cl, int cr)
{
    int mid = (cl + cr) >> 1;
    if (tree[rt].lazy)
    {
        tree[rt << 1].lazy += tree[rt].lazy;
        tree[rt << 1 | 1].lazy += tree[rt].lazy;
        tree[rt << 1].sum += tree[rt].lazy * (mid - cl + 1);
        tree[rt << 1 | 1].sum += tree[rt].lazy * (cr - mid);
        tree[rt].lazy = 0;
    }
    return;
}
void build(int rt, int cl, int cr)
{
    if (cl == cr)
    {
        tree[rt] = {a[cl], 0};
        return;
    }
    int mid = (cl + cr) >> 1;
    build(rt << 1, cl, mid);
    build(rt << 1 | 1, mid + 1, cr);
    pushup(rt);
}
void update(int pos, int val, int rt, int cl, int cr)
{
    if (cl == cr)
    {
        tree[rt].sum += val;
        return;
    }
    int mid = (cl + cr) >> 1;
    if (pos <= mid)
        update(pos, val, rt << 1, cl, mid);
    else
        update(pos, val, rt << 1 | 1, mid + 1, cr);
    pushup(rt);
    return;
}
void update(int l, int r, int val, int rt, int cl, int cr)
{
    if (l <= cl && cr <= r)
    {
        tree[rt].sum += val * (cr - cl + 1);
        tree[rt].lazy += val;
        return;
    }
    pushdown(rt, cl, cr);
    int mid = (cl + cr) >> 1;
    if (l <= mid)
        update(l, r, val, rt << 1, cl, mid);
    if (r > mid)
        update(l, r, val, rt << 1 | 1, mid + 1, cr);
    pushup(rt);
}
int query(int l, int r, int rt, int cl, int cr)
{
    if (l <= cl && cr <= r)
    {
        return tree[rt].sum;
    }
    pushdown(rt, cl, cr);
    int res = 0;
    int mid = (cl + cr) >> 1;
    if (l <= mid)
        res += query(l, r, rt << 1, cl, mid);
    if (r > mid)
        res += query(l, r, rt << 1 | 1, mid + 1, cr);
    return res;
}
signed main()
{
    int n;
    cin >> n;
    int q;
    cin >> q;
    for (int i = 1; i <= n; i++)
    {
        int x;
        cin >> x;
        update(i, x, 1, 1, n);
    }
    while (q--)
    {
        int op;
        cin >> op;
        if (op == 1)
        {
            int l, r, d;
            cin >> l >> r >> d;
            update(l, r, d, 1, 1, n);
        }
        else
        {
            int l, r;
            cin >> l >> r;
            cout << query(l, r, 1, 1, n) << endl;
        }
    }
    return 0;
}

1.3 普通线段树（静态区间加、区间乘，非永久化）

贴出来记得懒标记顺序思考问题。注意，懒标记下传的时候是 $f_{rt}\ \circ \ f_{sons}$ 的复合函数顺序。根据Segtrees.h思想思考。

#include <bits/stdc++.h>
#include <icpc-model/Modint.h>
using namespace Modint;
using namespace std;
#define int long long
using mint = MLong<0>;
struct node
{
    mint sum;
    mint lazyadd = 0;
    mint lazymul = 1;
};
const int maxn = 2e5 + 9;
node tree[maxn << 2];
mint a[maxn];
void pushup(int rt)
{
    tree[rt].sum = tree[rt << 1].sum + tree[rt << 1 | 1].sum;
    return;
}
void pushdown(int rt, int cl, int cr)
{
    // 儿子节点已有ax+b,传下来c(ax+b)+d=cax+cb+d);
    int mid = (cl + cr) >> 1;
    if (tree[rt].lazyadd != 0 || tree[rt].lazymul != 1)
    {
        tree[rt << 1].lazyadd *= tree[rt].lazymul;
        tree[rt << 1].lazyadd += tree[rt].lazyadd;

        tree[rt << 1 | 1].lazyadd *= tree[rt].lazymul;
        tree[rt << 1 | 1].lazyadd += tree[rt].lazyadd;

        tree[rt << 1].lazymul *= tree[rt].lazymul;
        tree[rt << 1 | 1].lazymul *= tree[rt].lazymul;

        tree[rt << 1].sum = tree[rt << 1].sum * tree[rt].lazymul + tree[rt].lazyadd * (mid - cl + 1);
        tree[rt << 1 | 1].sum = tree[rt << 1 | 1].sum * tree[rt].lazymul + tree[rt].lazyadd * (cr - mid);
        tree[rt].lazyadd = 0;
        tree[rt].lazymul = 1;
    }

    return;
}
void build(int rt, int cl, int cr)
{
    if (cl == cr)
    {
        tree[rt].sum = a[cl];
        return;
    }
    int mid = (cl + cr) >> 1;
    build(rt << 1, cl, mid);
    build(rt << 1 | 1, mid + 1, cr);
    pushup(rt);
}
void update(int l, int r, int add, int mul, int rt, int cl, int cr)
{
    if (l <= cl && cr <= r)
    {
        tree[rt].sum *= mul;
        tree[rt].sum += add * (cr - cl + 1);

        tree[rt].lazyadd *= mul;
        tree[rt].lazyadd += add;

        tree[rt].lazymul *= mul;

        return;
    }
    pushdown(rt, cl, cr);
    int mid = (cl + cr) >> 1;
    if (l <= mid)
        update(l, r, add, mul, rt << 1, cl, mid);
    if (r > mid)
        update(l, r, add, mul, rt << 1 | 1, mid + 1, cr);
    pushup(rt);
}
mint query(int l, int r, int rt, int cl, int cr)
{
    if (l <= cl && cr <= r)
    {
        return tree[rt].sum;
    }
    pushdown(rt, cl, cr);
    mint res = 0;
    int mid = (cl + cr) >> 1;
    if (l <= mid)
        res += query(l, r, rt << 1, cl, mid);
    if (r > mid)
        res += query(l, r, rt << 1 | 1, mid + 1, cr);
    return res;
}
signed main()
{
    int n;
    cin >> n;
    int q;
    cin >> q;
    int m;
    cin >> m;
    mint::setMod(m);
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
    }
    build(1, 1, n);
    while (q--)
    {
        int op;
        cin >> op;
        if (op == 1)
        {
            int l, r, d;
            cin >> l >> r >> d;
            update(l, r, 0, d, 1, 1, n);
            /*for (int i = 1; i <= n; i++)
            {
                cout << query(i, i, 1, 1, n) << " ";
            }
            cout << endl;*/
        }
        else if (op == 2)
        {
            int l, r, d;
            cin >> l >> r >> d;
            update(l, r, d, 1, 1, 1, n);
            /*for (int i = 1; i <= n; i++)
            {
                cout << query(i, i, 1, 1, n) << " ";
            }
            cout << endl;*/
        }
        else
        {
            int l, r;
            cin >> l >> r;
            cout << query(l, r, 1, 1, n) << endl;
        }
    }
    return 0;
}

1.4 Segtree.h/lazy_segtree

ACLibrary线段树，非递归模式，线段树下标从0开始。下文所提及区间默认左闭右开。

函数列表

bit_ceil : 取比参数大的最近的 $2^n$

countr_zero : 取参数的二进制结尾有多少个 $0$

pushup : 字面含义

upd : 修改完整线段树节点所代表区间

pushdown ：字面含义

explicit lazy_segtree(const vector<S> &v) : 构造函数

void set(int p, S x) : 单点修改为 $x$ （单点改为）

S get(int p) : 单点查询

S query(int l, int r) : 查询区间 $[l,r)$ 进行 $op$ 的结果

void modify(int p, F f) : 单点应用修改（单点加）

void modify(int l, int r, F f) : 区间 $[l,r)$ 应用修改 (区间加)

template <bool (*g)(S)> int max_right(int l) : 线段树二分查询从 $l$ 开始的最右端点 $r$ ，满足 $g(op[l,l+1,\cdots,\textcolor{red}{r-1}])=true$ .

template <bool (*g)(S)> int min_left(int r) : 线段树二分查询到 $r$ 的最左端点 $l$ ，满足 $g(op[l,l+1,\cdots,\textcolor{red}{r-1}])=true$ .

#include<bits/stdc++.h>
using namespace std;
namespace Segtrees
{
    int bit_ceil(int n)
    {
        int x = 1;
        while (x < n)
            x *= 2;
        return x;
    }
    int countr_zero(unsigned int n)
    {
        return __builtin_ctz(n);
    }
    template <class S,S (*op)(S, S),S (*e)(),class F,S (*mp)(F, S),F (*comp)(F, F),F (*id)()>
    struct lazy_segtree
    {
    private:
        int _n, size, log;
        vector<S> d;
        vector<F> lz;
        void pushup(int k) { d[k] = op(d[k << 1], d[k << 1 | 1]); }
        void upd(int k, F f)
        {
            d[k] = mp(f, d[k]);
            if (k < size)
                lz[k] = comp(f, lz[k]);
        }
        void pushdown(int k)
        {
            upd(k << 1, lz[k]);
            upd(k << 1 | 1, lz[k]);
            lz[k] = id();
        }

    public:
        lazy_segtree() : lazy_segtree(0) {}
        explicit lazy_segtree(int n) : lazy_segtree(vector<S>(n, e())) {}
        explicit lazy_segtree(const vector<S> &v) : _n(int(v.size()))
        {
            size = bit_ceil((_n));
            log = countr_zero(size);
            d = vector<S>(2 * size, e());
            lz = vector<F>(size, id());
            for (int i = 0; i < _n; i++)
                d[size + i] = v[i];
            for (int i = size - 1; i >= 1; i--)
            {
                pushup(i);
            }
        }
        void set(int p, S x)
        {
            assert(0 <= p && p < _n);
            p += size;
            for (int i = log; i >= 1; i--)
                pushdown(p >> i);
            d[p] = x;
            for (int i = 1; i <= log; i++)
                pushup(p >> i);
        }
        S get(int p)
        {
            assert(0 <= p && p < _n);
            p += size;
            for (int i = log; i >= 1; i--)
                pushdown(p >> i);
            return d[p];
        }
        /*查询区间[l,r)的结果,l=r时返回幺元*/
        S query(int l, int r)
        {
            assert(0 <= l && l <= r && r <= _n);
            if (l == r)
                return e();
            l += size;
            r += size;
            for (int i = log; i >= 1; i--)
            {
                if (((l >> i) << i) != l)
                    pushdown(l >> i);
                if (((r >> i) << i) != r)
                    pushdown((r - 1) >> i);
            }
            S sml = e(), smr = e();
            while (l < r)
            {
                if (l & 1)
                    sml = op(sml, d[l++]);
                if (r & 1)
                    smr = op(d[--r], smr);
                l >>= 1;
                r >>= 1;
            }
            return op(sml, smr);
        }
        S all_query() { return d[1]; }
        void modify(int p, F f)
        {
            assert(0 <= p && p < _n);
            p += size;
            for (int i = log; i >= 1; i--)
                pushdown(p >> i);
            d[p] = mp(f, d[p]);
            for (int i = 1; i <= log; i++)
                pushup(p >> i);
        }
        void modify(int l, int r, F f)
        {
            assert(0 <= l && l <= r && r <= _n);
            if (l == r)
                return;
            l += size;
            r += size;
            for (int i = log; i >= 1; i--)
            {
                if (((l >> i) << i) != l)
                    pushdown(l >> i);
                if (((r >> i) << i) != r)
                    pushdown((r - 1) >> i);
            }
            int l2 = l, r2 = r;
            while (l < r)
            {
                if (l & 1)
                    upd(l++, f);
                if (r & 1)
                    upd(--r, f);
                l >>= 1;
                r >>= 1;
            }
            l = l2;
            r = r2;
            for (int i = 1; i <= log; i++)
            {
                if (((l >> i) << i) != l)
                    pushup(l >> i);
                if (((r >> i) << i) != r)
                    pushup((r - 1) >> i);
            }
        }
        /*
         * @brief 线段树二分，查询区间[l,n)满足g的最右端点r
         * @tparam G 查询函数g，参数类型S
         * @param l 区间左端点
         * @return 区间[l,n)满足g( op([l,l+1,···,r) )的最右端点r
         */
        template <bool (*g)(S)>
        int max_right(int l)
        {
            return max_right(l, [](S x)
                             { return g(x); });
        }
        template <class G>
        int max_right(int l, G g)
        {
            assert(0 <= l && l <= _n);
            assert(g(e()));
            if (l == _n)
                return _n;
            l += size;
            for (int i = log; i >= 1; i--)
                pushdown(l >> i);
            S sm = e();
            do
            {
                while (l % 2 == 0)
                    l >>= 1;
                if (!g(op(sm, d[l])))
                {
                    while (l < size)
                    {
                        pushdown(l);
                        l = (2 * l);
                        if (g(op(sm, d[l])))
                        {
                            sm = op(sm, d[l]);
                            l++;
                        }
                    }
                    return l - size;
                }
                sm = op(sm, d[l]);
                l++;
            } while ((l & -l) != l);
            return _n;
        }
        template <bool (*g)(S)>
        int min_left(int r)
        {
            return min_left(r, [](S x)
                            { return g(x); });
        }
        template <class G>
        int min_left(int r, G g)
        {
            assert(0 <= r && r <= _n);
            assert(g(e()));
            if (r == 0)
                return 0;
            r += size;
            for (int i = log; i >= 1; i--)
                pushdown((r - 1) >> i);
            S sm = e();
            do
            {
                r--;
                while (r > 1 && (r % 2))
                    r >>= 1;
                if (!g(op(d[r], sm)))
                {
                    while (r < size)
                    {
                        pushdown(r);
                        r = (2 * r + 1);
                        if (g(op(d[r], sm)))
                        {
                            sm = op(d[r], sm);
                            r--;
                        }
                    }
                    return r + 1 - size;
                }
                sm = op(d[r], sm);
            } while ((r & -r) != r);
            return 0;
        }
};

1.5 Segtree.h/segtree

#include<bits/stdc++.h>
using namespace std;
namespace Segtrees
{
    template <class S, S (*op)(S, S), S (*e)()>
    struct segtree
    {
    public:
        segtree() : segtree(0) {}
        explicit segtree(int n) : segtree(vector<S>(n, e())) {}
        explicit segtree(const vector<S> &v) : _n(v.size())
        {
            size = bit_ceil(_n);
            log = countr_zero(size);
            d = vector<S>(2 * size, e());
            for (int i = 0; i < _n; i++)
                d[size + i] = v[i];
            for (int i = size - 1; i >= 1; i--)
            {
                pushup(i);
            }
        }
        void set(int p, S x)
        {
            assert(0 <= p && p < _n);
            p += size;
            d[p] = x;
            for (int i = 1; i <= log; i++)
                pushup(p >> i);
        }
        S get(int p) const
        {
            assert(0 <= p && p < _n);
            return d[p + size];
        }
        S query(int l, int r) const
        {
            assert(0 <= l && l <= r && r <= _n);
            S sml = e(), smr = e();
            l += size;
            r += size;

            while (l < r)
            {
                if (l & 1)
                    sml = op(sml, d[l++]);
                if (r & 1)
                    smr = op(d[--r], smr);
                l >>= 1;
                r >>= 1;
            }
            return op(sml, smr);
        }
        S all_query() const { return d[1]; }
        template <bool (*f)(S)>
        int max_right(int l) const
        {
            return max_right(l, [](S x)
                             { return f(x); });
        }
        template <class F>
        int max_right(int l, F f) const
        {
            assert(0 <= l && l <= _n);
            assert(f(e()));
            if (l == _n)
                return _n;
            l += size;
            S sm = e();
            do
            {
                while (l % 2 == 0)
                    l >>= 1;
                if (!f(op(sm, d[l])))
                {
                    while (l < size)
                    {
                        l = (2 * l);
                        if (f(op(sm, d[l])))
                        {
                            sm = op(sm, d[l]);
                            l++;
                        }
                    }
                    return l - size;
                }
                sm = op(sm, d[l]);
                l++;
            } while ((l & -l) != l);
            return _n;
        }
        template <bool (*f)(S)>
        int min_left(int r) const
        {
            return min_left(r, [](S x)
                            { return f(x); });
        }
        template <class F>
        int min_left(int r, F f) const
        {
            assert(0 <= r && r <= _n);
            assert(f(e()));
            if (r == 0)
                return 0;
            r += size;
            S sm = e();
            do
            {
                r--;
                while (r > 1 && (r % 2))
                    r >>= 1;
                if (!f(op(d[r], sm)))
                {
                    while (r < size)
                    {
                        r = (2 * r + 1);
                        if (f(op(d[r], sm)))
                        {
                            sm = op(d[r], sm);
                            r--;
                        }
                    }
                    return r + 1 - size;
                }
                sm = op(d[r], sm);
            } while ((r & -r) != r);
            return 0;
        }

    private:
        int _n, size, log;
        vector<S> d;
        void pushup(int k) { d[k] = op(d[2 * k], d[2 * k + 1]); }
    };
};

1.6 线段树合并

动态开点线段树合并，常出现于树上问题，父亲节点继承子节点信息。树上差分结合线段树合并维护路径上信息。

示例是非永久化标记的写法。核心就这一个，具体可参考主席树写法。

int merge(int rt1, int rt2, int cl, int cr)
{
    if (!rt1 || !rt2)
        return rt1 | rt2;
    if (cl == cr)
    {
        tree[rt1].maxnum += tree[rt2].maxnum;
        return rt1;
    }
    int mid = (cl + cr) >> 1;
    tree[rt1].l = merge(tree[rt1].l, tree[rt2].l, cl, mid);
    tree[rt1].r = merge(tree[rt1].r, tree[rt2].r, mid + 1, cr);
    pushup(rt1);
    return rt1;
}

裸模板见下面线段树分裂中，有线段树合并部分。

自己风格的主席树是用线段树合并写的，思路更清晰。

1.7 线段树分裂

八辈子碰不上一个。

给出一个可重集 $a$ （编号为 $1$ ），它支持以下操作：

0 p x y：将可重集 $p$ 中大于等于 $x$ 且小于等于 $y$ 的值移动到一个新的可重集中（新可重集编号为从 $2$ 开始的正整数，是上一次产生的新可重集的编号+1）。

1 p t：将可重集 $t$ 中的数放入可重集 $p$ ，且清空可重集 $t$ （数据保证在此后的操作中不会出现可重集 $t$ ）。

2 p x q：在 $p$ 这个可重集中加入 $x$ 个数字 $q$ 。

3 p x y：查询可重集 $p$ 中大于等于 $x$ 且小于等于 $y$ 的值的个数。

4 p k：查询在 $p$ 这个可重集中第 $k$ 小的数，不存在时输出 -1。

// 线段树分裂
// 线段树合并逆向操作
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define IOS ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
// #define DEBUG 1
const int maxn = 3e5 + 9;
int n, m, tot = 0, root[maxn], a[maxn];
struct node
{
    int l, r, sum;
    int cl, cr;
} tree[maxn << 5];
#define ls(rt) tree[rt].l
#define rs(rt) tree[rt].r
#define rcl(rt) tree[rt].cl
#define rcr(rt) tree[rt].cr
#define sum(rt) tree[rt].sum
void pushup(int rt)
{
    sum(rt) = sum(ls(rt)) + sum(rs(rt));
}
void update(int &rt, int num, int pos, int cl = 1, int cr = n) // 单点修改权值线段树
{
    if (!rt)
    {
        rt = ++tot;
        rcl(rt) = cl, rcr(rt) = cr;
    }
    if (cl == cr)
    {
        sum(rt) += num;
        return;
    }
    int mid = (cl + cr) >> 1;
    if (pos <= mid)
        update(ls(rt), num, pos, cl, mid);
    else
        update(rs(rt), num, pos, mid + 1, cr);
    pushup(rt);
    return;
}
int querykth(int &rt, int k, int cl = 1, int cr = n) // 查询区间第k小，线段树上二分
{
    if (!rt)
        return -1;
    if (cl == cr)
        return cl;
    int mid = (cl + cr) >> 1LL;
    if (sum(ls(rt)) >= k)
        return querykth(ls(rt), k, cl, mid);
    else
        return querykth(rs(rt), k - sum(ls(rt)), mid + 1, cr);
}
int queryinterval(int &rt, int l, int r, int cl = 1, int cr = n) // 查询大于等于x小于等于y的元素个数
{
    if (l <= cl && cr <= r)
        return sum(rt);
    int mid = (cl + cr) >> 1LL, ans = 0;
    if (l <= mid)
        ans += queryinterval(ls(rt), l, r, cl, mid);
    if (r > mid)
        ans += queryinterval(rs(rt), l, r, mid + 1, cr);
    return ans;
}
void segmerge(int &rt1, int &rt2, int cl = 1, int cr = n)
{
    if (!rt1 || !rt2)
        return void(rt1 = rt1 + rt2);
    if (cl == cr)
        return void(sum(rt1) += sum(rt2));
    int mid = (cl + cr) >> 1;
    segmerge(ls(rt1), ls(rt2), cl, mid);
    segmerge(rs(rt1), rs(rt2), mid + 1, cr);
    pushup(rt1);
    return;
}
void segsplit(int &rt1, int &rt2, int l, int r, int cl = 1, int cr = n)
{
    if (!rt1)
    {
        return;
    }
    if (l <= cl && cr <= r)
    {
        rt2 = rt1;
        rt1 = 0;
        return;
    }
    if (!rt2)
    {
        rt2 = ++tot;
        rcl(rt2) = cl, rcr(rt2) = cr;
    }
    int mid = (cl + cr) >> 1;
    if (l <= mid)
        segsplit(ls(rt1), ls(rt2), l, r, cl, mid);
    if (r > mid)
        segsplit(rs(rt1), rs(rt2), l, r, mid + 1, cr);
    pushup(rt1);
    pushup(rt2);
    return;
}
int cnt = 1;
signed main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        update(root[1], a[i], i);
    }
    while (m--)
    {
        int op, x, y, z;
        cin >> op;
        switch (op)
        {
        case 0:
            cnt++;
            cin >> x >> y >> z;
            segsplit(root[x], root[cnt], y, z);
            break;
        case 1:
            cin >> x >> y;
            segmerge(root[x], root[y]);
            break;
        case 2:
            cin >> x >> y >> z;
            update(root[x], y, z);
            break;
        case 3:
            cin >> x >> y >> z;
            cout << queryinterval(root[x], y, z) << endl;
            break;
        case 4:
            cin >> x >> y;
            cout << querykth(root[x], y) << endl;
            break;
        }
    }
}

1.8 扫描线

1.8.1 求矩形面积的并

扫描线问题 切记切记 维护好什么时候扫过，扫过的部分怎么算，已经扫完的部分如何删除的边界问题，也是重点DEBUG部分.

求矩形面积的并每次查询的是整个区间内线段的长度。

Codeforces上有一道维护线段的加入和删除，区间查询某个区间是否有线段覆盖的题，注意，如果涉及到此问题，仅扫描线思想中标记不下传只维护当前线段树结点所表示的完整区间是否有线段的类线段树分治思想还需要额外判定以下内容：

如果目标区间 $[l,r]$ 已经被某条长线段完整覆盖，直接返回 $true$ 即可。

// 扫描线模板
#include <bits/stdc++.h>
using namespace std;
#define i64 long long
struct segtrees
{
    int l, r;
    i64 sum = 0;
    int tags = 0;
};
const int maxn = 4e5 + 9;
segtrees tree[maxn << 2];
int n, m;
i64 points[maxn];
void update(int rt, int cl, int cr)
{
    if (tree[rt].tags)
    {
        tree[rt].sum = points[cr + 1] - points[cl];
        return;
    }
    tree[rt].sum = tree[rt << 1].sum + tree[rt << 1 | 1].sum;
    return;
}
void modifytags(int l, int r, int d, int rt, int cl, int cr)
{
    if (l <= cl && cr <= r)
    {
        tree[rt].tags += d;
        update(rt, cl, cr);
        return;
    }
    int mid = (cl + cr) >> 1;
    if (l <= mid)
        modifytags(l, r, d, rt << 1, cl, mid);
    if (r > mid)
        modifytags(l, r, d, rt << 1 | 1, mid + 1, cr);
    update(rt, cl, cr);
    return;
}
struct node
{
    int x1, y1, x2, y2;
} rem[maxn];
vector<tuple<int, int, int, int>> op;
signed main()
{
    cin >> n;
    int cnt = 0;
    int S = 0;
    for (int i = 1; i <= n; i++)
    {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        if (x1 > x2)
            swap(x1, x2);
        if (y1 > y2)
            swap(y1, y2);
        rem[i] = {x1, y1, x2, y2};
        points[++cnt] = x1;
        points[++cnt] = x2;
    }
    sort(points + 1, points + 1 + cnt);
    S = unique(points + 1, points + 1 + cnt) - points - 1;
    for (int i = 1; i <= n; i++)
    {
        int x1 = lower_bound(points + 1, points + 1 + S, rem[i].x1) - points;
        int x2 = lower_bound(points + 1, points + 1 + S, rem[i].x2) - points;
        op.push_back({rem[i].y1, x1, x2 - 1, 1});
        op.push_back({rem[i].y2, x1, x2 - 1, -1});
    }
    sort(op.begin(), op.end());
    i64 ans = 0;
    i64 last = 0;
    for (auto [y, x1, x2, d] : op)
    {
        ans += (y - last) * tree[1].sum;
        modifytags(x1, x2, d, 1, 1, S);
        last = y;
    }
    cout << ans << endl;
    return 0;
}

1.8.2 维护线段的并

其实有点废话，本质上不是扫描线，但是确实是通过维护线段区间的并判断此时有多少个合法情况，来源于牛客多校的 $Interval Selection$ :

有一个长度为 $n$ 的数组，当且仅当 $a_l,a_{l+1},\dots a_r$ 中的每个元素在当前区间内恰好出现 $k$ 次时，数组中的子数组 $[l,r]$ 才是好数组。

例如，对于 $a=[1,1,2,3,2,3,1]$ 和 $k=2$ ，区间 $[1,2]$ 、 $[3,6]$ 、 $[1,6]$ 等都是好的。但是， $[1,3]$ 不符合条件，因为元素 $2$ 只出现了一次； $[1,7]$ 不符合条件，因为元素 $1$ 出现了 $3$ 次。

请找出可以选择的好区间的个数。

通过线段并维护不合法区间数量即可，线段交过于难以维护。

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS                      \
    ios::sync_with_stdio(false); \
    cin.tie(0);                  \
    cout.tie(0);
const int maxn = 2e5 + 9;
int a[maxn], b[maxn];
struct node
{
    int l;
    int r;
    int cover;
    int sum;
} tree[maxn << 2LL];
int n;
#define ls(rt) tree[rt << 1LL]
#define rs(rt) tree[rt << 1LL | 1]
#define cover(rt) tree[rt].cover
#define sum(rt) tree[rt].sum
#define getl(rt) tree[rt].l
#define getr(rt) tree[rt].r
void pushup(int rt)
{
    if (cover(rt))
        sum(rt) = 0;
    else if (getl(rt) == getr(rt))
    {
        sum(rt) = 1;
    }
    else
        sum(rt) = sum(rt << 1LL) + sum(rt << 1LL | 1);
    return;
}
void modify(int l, int r, int d, int rt = 1, int cl = 1, int cr = n)
{
    if (l <= cl && cr <= r)
    {
        cover(rt) += d;
        pushup(rt);
        return;
    }
    int mid = (cl + cr) >> 1;
    if (l <= mid)
        modify(l, r, d, rt << 1LL, cl, mid);
    if (r > mid)
        modify(l, r, d, rt << 1LL | 1, mid + 1, cr);
    pushup(rt);
    return;
}
int querysum(int l, int r, int rt = 1, int cl = 1, int cr = n)
{
    if (cover(rt))
        return 0;
    if (l <= cl && cr <= r)
    {
        return sum(rt);
    }
    int mid = (cl + cr) >> 1;
    int ans = 0;
    if (l <= mid)
        ans += querysum(l, r, rt << 1LL, cl, mid);
    if (r > mid)
        ans += querysum(l, r, rt << 1LL | 1, mid + 1, cr);
    return ans;
}
void build(int rt = 1, int l = 1, int r = n)
{
    getl(rt) = l;
    getr(rt) = r;
    cover(rt) = 0;
    if (l == r)
    {
        sum(rt) = 1;
        return;
    }
    int mid = (l + r) >> 1;
    build(rt << 1LL, l, mid);
    build(rt << 1LL | 1, mid + 1, r);
    pushup(rt);
    return;
}
int k;
vector<int> rem[maxn];
void solve()
{
    cin >> n >> k;
    build();
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        b[i] = a[i];
    }
    sort(b + 1, b + n + 1);
    int m = unique(b + 1, b + n + 1) - b - 1;
    for (int i = 1; i <= m; i++)
    {
        rem[i].clear();
    }
    for (int i = 1; i <= n; i++)
    {
        a[i] = lower_bound(b + 1, b + m + 1, a[i]) - b;
    }
    int ans = 0;
    for (int i = 1; i <= n; i++)
    {
        if (rem[a[i]].empty())
        {
            rem[a[i]].push_back(0);
        }
        rem[a[i]].push_back(i);
        int t = rem[a[i]].size() - 1;
        int l = rem[a[i]][t - 1] + 1, r = rem[a[i]][t];
        modify(l, r, 1);
        if (t >= k)
        {
            l = rem[a[i]][t - k] + 1;
            r = rem[a[i]][t - k + 1];
            modify(l, r, -1);
            if (l >= 2)
                modify(1, l - 1, 1);
            ans += querysum(l, r);
        }
    }
    cout << ans << endl;
    return;
}
signed main()
{
    IOS;
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

1.9 主席树（静态区间第k小、小于等于第k小的和、小于等于前k小有多少个数）

记住主席树的根本思想在于维护前缀和。

另外，主席树复杂度 $O(Knlogn)$ ，常数较大， $n\le 5e5$ 时如果确定必须用到主席树，算法复杂度必须严格纯 $O(nlogn)$ ， $O(nlog^2n)$ 可能会 $\color{red}TLE$

附议：其实主席树根本就不需要离散化，动态开点的属性确保了树深度最多 $logV$ ，一共 $10^5$ 级别的数字确保了最多 $O(nlogV)$ 的空间复杂度，一定不会超，就是常数稍微大一点而已。这意味着主席树可以完全做到平替 $01Trie$ 求异或最值问题。

#include <bits/stdc++.h>
using namespace std;
#define i64 long long
struct node
{
    int l, r;
    i64 sum;
    i64 cnt;
};
int tot = 0;
const int maxn = 5e5 + 9;
i64 bs[maxn]; // 离散化数组，下标离散化，内存为原数字
i64 a[maxn];
node tree[maxn << 5];
int root[maxn];
void init(int n)
{
    for (int i = 0; i <= n; i++)
    {
        root[i] = 0;
    }
    tot = 0;
    return;
}
int newnode()
{
    tot++;
    tree[tot] = {0, 0, 0, 0};
    return tot;
}
void update(int &rt, int pos, int cl, int cr)
{
    if (!rt)
    {
        rt = newnode();
    }
    tree[rt].cnt++;
    tree[rt].sum += bs[pos];
    if (cl == cr)
    {
        return;
    }
    int mid = (cl + cr) >> 1;
    if (pos <= mid)
        update(tree[rt].l, pos, cl, mid);
    else
        update(tree[rt].r, pos, mid + 1, cr);
}
void merge(int &rt1, int &rt2, int cl, int cr)
{
    if (!rt1 || !rt2)
    {
        rt1 |= rt2;
        return;
    }
    tree[rt1].cnt += tree[rt2].cnt;
    tree[rt1].sum += tree[rt2].sum;
    if (cl == cr)
    {
        return;
    }
    int mid = (cl + cr) >> 1;
    merge(tree[rt1].l, tree[rt2].l, cl, mid);
    merge(tree[rt1].r, tree[rt2].r, mid + 1, cr);
    return;
}
tuple<i64, i64, int> querykth(int rt1, int rt2, int k, int cl, int cr)
{
    if (cl == cr)
    {
        return {bs[cl], tree[rt2].sum - tree[rt1].sum, tree[rt2].cnt - tree[rt1].cnt};
    }
    int mid = (cl + cr) >> 1;
    int nowcnt = tree[tree[rt2].l].cnt - tree[tree[rt1].l].cnt;
    i64 nowsum = tree[tree[rt2].l].sum - tree[tree[rt1].l].sum;
    if (nowcnt >= k)
        return querykth(tree[rt1].l, tree[rt2].l, k, cl, mid);
    auto [kthrl, rsum, rcnt] = querykth(tree[rt1].r, tree[rt2].r, k - nowcnt, mid + 1, cr);
    return {kthrl, nowsum + rsum, nowcnt + rcnt};
}
int sz = 0;

附：关于主席树的内存回收问题

需要打标记，一个想删除的点可以被删除当且仅当任何版本都没有再使用这个点。尤其注意merge函数的处理问题。理论上涉及主席树老版本删除删除的题目，不应当在内存上进行卡制无内存回收无法通过的数据。

int newnode()
{
    if (tot + 1 < inf)
        tot++;
    else
        tot = qs.front(), qs.pop();
    viscnt[tot]++;
    tree[tot] = {0, 0, 0};
    return tot;
}
void del_tree(int rt)
{
    if (!rt)
        return;
    del_tree(tree[rt].l);
    del_tree(tree[rt].r);
    viscnt[rt]--;
    if (!viscnt[rt])
    {
        qs.push(rt);
        tree[rt] = {0, 0, 0};
    }
    return;
}

1.10 主席树维护区间本质不同的元素个数（HH的项链）

给定数组 $a$ ，每次询问 $[l,r]$ 中有多少个不同元素的值出现？

一个 $trival$ 的做法是数每个元素最后一次出现的那一个。主席树下标开位置，记录该位置是否有颜色。

记录颜色 $k$ 最后一次出现的位置为 $pre_k$ ，当前为 $i$ 位置，颜色为 $k$ ，则将 $pos=pre_k$ 位置的线段树节点 $-1$ 表示该位置不再计算， $pos=i$ 位置节点 $+1$ 表示该节点计算颜色，更新 $pre_k=i$ 。询问 $[l,r]$ 时查询 $root[r]$ 版本主席树。

第一种做法有点像树状数组离线扫描线，不再写。

第二个更Trival的主席树做法：

数每个元素数最左侧出现的那一个。思考， $[l,r]$ 中位置 $i$ 上的元素如果做出贡献，那么记 $pre_i$ 为位置 $i$ 上的颜色在 $i$ 前最后一次出现的位置，第一次出现时记作 $pre_i=0$ ，则必然有 $pre_i<l$ .

对位置开权值树桶，维护 $pre$ 数组中值 $v=pre[i]$ 出现了多少次。查询区间 $[l,r]$ ，则主席树查询 $root[l-1]$ 和 $root[r]$ 的差中，小于 $l$ 的值的和。注意，权树下标从 $0$ 开始，因保证 $pre_i=0$ 表示位置 $i$ 上的颜色在整个序列中第一次出现。

第二种方法更方便于维护一些被求和的东西。

1.11 主席树二维数点（HEOI2017, SuperBig常数，不推荐，建议离线树状数组扫描线，这里主要贴出来主席树构建时有区间update标记永久化）

#include <bits/stdc++.h>
using namespace std;
#define int long long
struct Segtree_presistent
{
    struct node
    {
        int l = 0, r = 0;
        int sum = 0;
        int lazy = 0;
    };
    vector<node> t;
    vector<int> root;
    int cnt = 0, n = 0;
    void init(int _n)
    {
        n = _n;
        cnt = 0;
        root.assign(n + 1, 0);
        t.assign(32 * n + 10, node());
    }
    void modify(int &rt, int l, int r, int d, int cl, int cr)
    {
        if (!rt)
        {
            rt = ++cnt;
        }
        t[rt].sum += 1ll * d * (min(r, cr) - max(l, cl) + 1);
        if (l <= cl && cr <= r)
        {
            t[rt].lazy += d;
            return;
        }
        int mid = (cl + cr) >> 1ll;
        if (l <= mid)
            modify(t[rt].l, l, r, d, cl, mid);
        if (r > mid)
            modify(t[rt].r, l, r, d, mid + 1, cr);
        return;
    }
    int query(int rt, int l, int r, int cl, int cr)
    {
        if (!rt)
            return 0;
        if (l <= cl && cr <= r)
        {
            return t[rt].sum;
        }
        int mid = (cl + cr) >> 1ll;
        int res = 0;
        if (l <= mid)
            res += query(t[rt].l, l, r, cl, mid);
        if (r > mid)
            res += query(t[rt].r, l, r, mid + 1, cr);
        return res + 1ll * (min(r, cr) - max(l, cl) + 1) * t[rt].lazy;
    }
    void merge(int &rt1, int &rt2, int cl, int cr)
    {
        if (!rt1 || !rt2)
        {
            rt1 = rt1 + rt2;
            return;
        }
        t[rt1].sum += t[rt2].sum;
        t[rt1].lazy += t[rt2].lazy;
        if (cl == cr)
            return;
        int mid = (cl + cr) >> 1ll;
        merge(t[rt1].l, t[rt2].l, cl, mid);
        merge(t[rt1].r, t[rt2].r, mid + 1, cr);
        return;
    }
};
Segtree_presistent seg;
const int maxn = 1e6 + 9;
struct interval
{
    int l, r;
    int w;
};
struct Edge
{
    int n;
    vector<vector<interval>> G;
    void init(int _n)
    {
        n = _n;
        G.assign(n + 1, vector<interval>());
    }
    void add_edge(int u, int l, int r, int w)
    {
        G[u].push_back({l, r, w});
    }
};
Edge G;
int a[maxn];
int l[maxn], r[maxn];
stack<int> s;
int n, m, p, q;
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin >> n >> m >> p >> q;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        l[i] = 0, r[i] = n + 1;
    }
    for (int i = 1; i <= n; i++)
    {
        while (!s.empty() && a[s.top()] < a[i])
        {
            s.pop();
        }
        l[i] = s.empty() ? 0ll : s.top();
        s.push(i);
    }
    while (!s.empty())
    {
        s.pop();
    }
    for (int i = n; i >= 1; i--)
    {
        while (!s.empty() && a[s.top()] < a[i])
        {
            s.pop();
        }
        r[i] = s.empty() ? 1ll * n + 1 : s.top();
        s.push(i);
    }
    seg.init(n);
    G.init(n);
    for (int i = 1; i <= n; i++)
    {
        if (i != n)
        {
            G.add_edge(i, i + 1, i + 1, p);
        }
        if (l[i] && r[i] <= n)
            G.add_edge(l[i], r[i], r[i], p);
        if (l[i] && i + 1 <= r[i] - 1)
        {
            G.add_edge(l[i], i + 1, r[i] - 1, q);
        }
        if (r[i] <= n && l[i] + 1 <= i - 1)
        {
            G.add_edge(r[i], l[i] + 1, i - 1, q);
        }
    }
    for (int i = 1; i <= n; i++)
    {
        for (auto [l, r, w] : G.G[i])
        {
            seg.modify(seg.root[i], l, r, w, 1, seg.n);
        }
        seg.merge(seg.root[i], seg.root[i - 1], 1, seg.n);
    }
    for (int i = 1; i <= m; i++)
    {
        int l, r;
        cin >> l >> r;
        cout << seg.query(seg.root[r], l, r, 1, seg.n) - seg.query(seg.root[l - 1], l, r, 1, seg.n) << endl;
    }
    return 0;
}

1.12 带修主席树/树套树（动态区间第k小，单点修改）

1.12.1 动态区间第k小

这个看怎么理解了，严格意义上根本不算主席树，属于树状数组套权值线段树。但是如果按前缀和理解主席树，merge函数视作对各个独立根的树求前缀和，树状数组就像是之前暴力预处理前缀和变成了将树直接绑在树状数组上，用树状数组求前缀和，也算说得过去。

理论上区间修改也可以？

注意潜在的空间爆炸问题。

(显然可以，具体实现参考1.11区间加，1.2区间乘，相同逻辑)

#include <bits/stdc++.h>
using namespace std;
const int maxn = 5e5 + 9;
#define int long long
int n;
struct node
{
    int l, r;
    int sum;
};
node tree[maxn << 5];
int tot = 0;
int root[maxn];
int sz;
int bs[maxn];
int a[maxn];
int q;
int cnt = 0;
int lowbit(int x)
{
    return (x & -x);
}
int newnode()
{
    tot++;
    tree[tot] = {0, 0, 0ll};
    return tot;
}
void upd(int &rt, int pos, int val, int cl, int cr)
{
    if (!rt)
    {
        rt = newnode();
    }
    tree[rt].sum += val;
    if (cl == cr)
        return;
    int mid = (cl + cr) >> 1;
    if (pos <= mid)
        upd(tree[rt].l, pos, val, cl, mid);
    else
        upd(tree[rt].r, pos, val, mid + 1, cr);
    return;
}
void update(int realrt, int val)
{
    for (int i = realrt; i <= n; i += lowbit(i))
    {
        upd(root[i], a[realrt], val, 1, sz);
    }
}
int query(vector<int> &rt1s, vector<int> &rt2s, int k, int cl, int cr)
{
    if (cl == cr)
        return cl;
    int mid = (cl + cr) >> 1;
    int sums = 0;
    for (auto j : rt2s)
        sums += tree[tree[j].l].sum;
    for (auto j : rt1s)
        sums -= tree[tree[j].l].sum;
    if (sums >= k)
    {
        for (auto &j : rt2s)
            j = tree[j].l;
        for (auto &j : rt1s)
            j = tree[j].l;
        return query(rt1s, rt2s, k, cl, mid);
    }
    else
    {
        for (auto &j : rt2s)
            j = tree[j].r;
        for (auto &j : rt1s)
            j = tree[j].r;
        return query(rt1s, rt2s, k - sums, mid + 1, cr);
    }
}
int querykth(int l, int r, int k)
{
    vector<int> rt1, rt2;
    for (int i = r; i; i -= lowbit(i))
    {
        rt2.push_back(root[i]);
    }
    for (int i = l - 1; i; i -= lowbit(i))
    {
        rt1.push_back(root[i]);
    }
    return query(rt1, rt2, k, 1, sz);
}

struct qs
{
    int l, r, k;
};
struct cs
{
    int pos, val;
};
signed main()
{
    cin >> n >> q;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        bs[++cnt] = a[i];
    }
    vector<tuple<char, qs, cs>> v(q + 1);
    for (int i = 1; i <= q; i++)
    {
        char c;
        cin >> c;
        if (c == 'Q')
        {
            int l, r, k;
            cin >> l >> r >> k;
            v[i] = {c, {l, r, k}, {}};
        }
        else
        {
            int pos, val;
            cin >> pos >> val;
            bs[++cnt] = val;
            v[i] = {c, {}, {pos, val}};
        }
    }
    sort(bs + 1, bs + 1 + cnt);
    sz = unique(bs + 1, bs + 1 + cnt) - bs - 1;
    for (int i = 1; i <= n; i++)
    {
        a[i] = lower_bound(bs + 1, bs + 1 + sz, a[i]) - bs;
        update(i, 1);
    }
    for (int i = 1; i <= q; i++)
    {
        auto [ch, qss, css] = v[i];
        if (ch == 'Q')
        {
            cout << bs[querykth(qss.l, qss.r, qss.k)] << endl;
        }
        else
        {
            update(css.pos, -1);
            a[css.pos] = lower_bound(bs + 1, bs + 1 + sz, css.val) - bs;
            update(css.pos, 1);
        }
    }
}

1.12.2 静态二维矩形第k小

空间复杂度极高。看数据范围是否选择范围分治。

#include <bits/stdc++.h>
using namespace std;
#define i64 int
struct node
{
    int l, r;
    int sum;
    int cnt;
};
const int maxn = 2e5 + 9;
node tree[maxn << 7];
int tot = 0;
const int sz = 1009;
int update(int rt, int pos, int cl, int cr)
{
    if (!rt)
        rt = ++tot;
    tree[rt].cnt++;
    tree[rt].sum += pos;
    if (cl == cr)
    {
        return rt;
    }
    int mid = (cl + cr) >> 1;
    if (pos <= mid)
        tree[rt].l = update(tree[rt].l, pos, cl, mid);
    else
        tree[rt].r = update(tree[rt].r, pos, mid + 1, cr);
    return rt;
}
int querysum(int &rt, int l, int r, int cl, int cr)
{
    if (!rt)
        return 0;
    if (l <= cl && cr <= r)
        return tree[rt].sum;
    int mid = (cl + cr) >> 1;
    int res = 0;
    if (l <= mid)
        res += querysum(tree[rt].l, l, r, cl, mid);
    if (r > mid)
        res += querysum(tree[rt].r, l, r, mid + 1, cr);
    return res;
}
struct Fenwick
{
private:
    int n, m;
    vector<vector<i64>> c;
    int lowbit(int x) { return x & -x; }

public:
    Fenwick(int n, int m) : n(n), m(m), c(n + 1, vector<i64>(m + 1, 0)) {}
    Fenwick() : n(0), m(0) {}
    void init(int n, int m)
    {
        this->n = n;
        this->m = m;
        c.assign(n + 1, vector<i64>(m + 1, 0));
    }
    void add(int x, int y, i64 v)
    {
        for (int i = x; i <= n; i += lowbit(i))
            for (int j = y; j <= m; j += lowbit(j))
                c[i][j] = update(c[i][j], v, 1, sz);
    }
    vector<int> query(int x, int y)
    {
        vector<int> res;
        for (int i = x; i; i -= lowbit(i))
            for (int j = y; j; j -= lowbit(j))
                res.push_back(c[i][j]);
        return res;
    }
};
int querysum(vector<int> &rt)
{
    int sum = 0;
    for (auto j : rt)
    {
        sum += tree[j].sum;
    }
    return sum;
}
int querycnt(vector<int> &rt)
{
    int sum = 0;
    for (auto j : rt)
    {
        sum += tree[j].cnt;
    }
    return sum;
}
int queryrcnt(vector<int> &rt)
{
    int sum = 0;
    for (auto j : rt)
    {
        sum += tree[tree[j].r].cnt;
    }
    return sum;
}
int queryrsum(vector<int> &rt)
{
    int sum = 0;
    for (auto j : rt)
    {
        sum += tree[tree[j].r].sum;
    }
    return sum;
}
void didl(vector<int> &rt)
{
    for (auto &j : rt)
    {
        j = tree[j].l;
    }
}
void didr(vector<int> &rt)
{
    for (auto &j : rt)
    {
        j = tree[j].r;
    }
}
int queryans(int h, int cl, int cr,
             vector<int> &rt1, vector<int> &rt2, vector<int> &rt3, vector<int> &rt4, int cnts)
{
    if (cl == cr)
    {
        int sums = querysum(rt1) + querysum(rt4) - querysum(rt2) - querysum(rt3);
        if (sums >= h)
        {
            int nowcnt = querycnt(rt1) + querycnt(rt4) - querycnt(rt2) - querycnt(rt3);
            while (nowcnt && sums - cl >= h)
                nowcnt--, sums -= cl;
            return cnts + nowcnt;
        }
        return -1;
    }
    int mid = (cl + cr) >> 1;
    int sum = queryrsum(rt1) + queryrsum(rt4) - queryrsum(rt2) - queryrsum(rt3);
    int newcnt = queryrcnt(rt1) + queryrcnt(rt4) - queryrcnt(rt2) - queryrcnt(rt3);
    if (sum >= h)
    {
        didr(rt1), didr(rt2), didr(rt3), didr(rt4);
        return queryans(h, mid + 1, cr, rt1, rt2, rt3, rt4, cnts);
    }
    else
    {
        didl(rt1), didl(rt2), didl(rt3), didl(rt4);
        return queryans(h - sum, cl, mid, rt1, rt2, rt3, rt4, cnts + newcnt);
    }
}
Fenwick fw;
int queryfinal(int x1, int x2, int y1, int y2, int h)
{
    vector<int> rt1, rt2, rt3, rt4;
    rt1 = fw.query(x1 - 1, y1 - 1);
    rt2 = fw.query(x2, y1 - 1);
    rt3 = fw.query(x1 - 1, y2);
    rt4 = fw.query(x2, y2);
    return queryans(h, 1, sz, rt1, rt2, rt3, rt4, 0);
}
signed main()
{
    int n, m, k;
    cin >> n >> m >> k;
    fw.init(n + 10, m + 10);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
        {
            int x;
            cin >> x;
            fw.add(i, j, x);
        }
    while (k--)
    {
        int x1, x2, y1, y2, h;
        cin >> x1 >> y1 >> x2 >> y2 >> h;
        int ans = queryfinal(x1, x2, y1, y2, h);
        if (ans > 0)
            cout << ans << endl;
        else
            cout << "Poor QLW" << endl;
    }
}

1.13 主席树可持久化数组

维护这样的一个长度为 $ N $ 的数组，支持如下几种操作

1
2
3

1. 对于操作1，格式为$ v_i \ 1 \ {loc}_i \ {value}_i $，即为在版本$ v_i $的基础上，将 $ a_{{loc}_i} $ 修改为 $ {value}_i $。

2. 对于操作2，格式为$ v_i \ 2 \ {loc}_i $，即访问版本$ v_i $中的 $ a_{{loc}_i} $的值，注意：**生成一样版本的对象应为 $v_i$**。

此外，每进行一次操作（对于操作2，即为生成一个完全一样的版本，不作任何改动），就会生成一个新的版本。版本编号即为当前操作的编号（从1开始编号，版本0表示初始状态数组）

注意和主席树不一样的地方，merge函数不赋值（因为是把剩下未变动的部分直接merge过来），修改时先改再merge，查询时先merge再改

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 2e6 + 9;
int tot = 0;
int sz;
struct node
{
    int l, r;
    int num;
};
node tree[maxn << 5];
int newnode()
{
    tot++;
    tree[tot] = {0, 0, 0};
    return tot;
}
void merge(int &rt1, int &rt2, int cl, int cr)
{
    if (!rt1 || !rt2)
    {
        rt1 |= rt2;
        return;
    }
    if (cl == cr)
    {
        // tree[rt1].num = tree[rt2].num;
        return;
    }
    int mid = (cl + cr) >> 1;
    merge(tree[rt1].l, tree[rt2].l, cl, mid);
    merge(tree[rt1].r, tree[rt2].r, mid + 1, cr);
    return;
}
void update(int &rt, int pos, int val, int cl, int cr)
{
    if (!rt)
        rt = newnode();
    if (cl == cr)
    {
        tree[rt].num = val;
        return;
    }
    int mid = (cl + cr) >> 1;
    if (pos <= mid)
        update(tree[rt].l, pos, val, cl, mid);
    else
        update(tree[rt].r, pos, val, mid + 1, cr);
}
int query(const int rt, int pos, int cl, int cr)
{
    if (!rt)
        return 0;
    if (cl == cr)
    {
        return tree[rt].num;
    }
    int mid = (cl + cr) >> 1;
    if (pos <= mid)
        return query(tree[rt].l, pos, cl, mid);
    else
        return query(tree[rt].r, pos, mid + 1, cr);
}
void printtree(int rt, int cl = 1, int cr = sz)
{
    if (!rt)
    {
        cout << 0 << endl;
        return;
    }
    if (cl == cr)
    {
        cout << tree[rt].num << endl;
        return;
    }
    int mid = (cl + cr) >> 1;
    printtree(tree[rt].l, cl, mid);
    printtree(tree[rt].r, mid + 1, cr);
}
int root[maxn];
int n, m;
int ver = 0;
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin >> n >> m;
    sz = n;
    for (int i = 1; i <= n; i++)
    {
        int val;
        cin >> val;
        update(root[0], i, val, 1, sz);
    }
    while (m--)
    {
        ver++;
        int v, op, pos, val;
        cin >> v >> op >> pos;
        if (op == 1)
        {
            cin >> val;
            update(root[ver], pos, val, 1, sz);
            merge(root[ver], root[v], 1, sz);
        }
        else
        {
            merge(root[ver], root[v], 1, sz);
            cout << query(root[ver], pos, 1, sz) << endl;
        }
    }
    return 0;
}

1.14 主席树可持久化并查集

给定 $n$ 个集合，第 $i$ 个集合内初始状态下只有一个数，为 $i$ 。

有 $m$ 次操作。操作分为 $3$ 种：

1 a b 合并 $a,b$ 所在集合；
2 k 回到第 $k$ 次操作（执行三种操作中的任意一种都记为一次操作）之后的状态；
3 a b 询问 $a,b$ 是否属于同一集合，如果是则输出 $1$ ，否则输出 $0$ 。

$n\le 10^5,m\le 10^5$

只需注意一个点，路径压缩并查集复杂度是均摊的，恶劣情况下单次合并会是 $O(n)$ 的复杂度。所以要上按秩合并（启发式合并）

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 2e5 + 9;
struct presistent_array
{
    int tot = 0;
    int sz;
    struct node
    {
        int l, r;
        int num;
    };
    node tree[maxn << 5];
    int newnode()
    {
        tot++;
        tree[tot] = {0, 0, 0};
        return tot;
    }
    void merge(int &rt1, int &rt2, int cl, int cr)
    {
        if (!rt1 || !rt2)
        {
            rt1 |= rt2;
            return;
        }
        if (cl == cr)
        {
            // tree[rt1].num = tree[rt2].num;
            return;
        }
        int mid = (cl + cr) >> 1;
        merge(tree[rt1].l, tree[rt2].l, cl, mid);
        merge(tree[rt1].r, tree[rt2].r, mid + 1, cr);
        return;
    }
    void update(int &rt, int pos, int val, int cl, int cr)
    {
        if (!rt)
            rt = newnode();
        if (cl == cr)
        {
            tree[rt].num = val;
            return;
        }
        int mid = (cl + cr) >> 1;
        if (pos <= mid)
            update(tree[rt].l, pos, val, cl, mid);
        else
            update(tree[rt].r, pos, val, mid + 1, cr);
    }
    int query(const int rt, int pos, int cl, int cr)
    {
        if (!rt)
            return 0;
        if (cl == cr)
        {
            return tree[rt].num;
        }
        int mid = (cl + cr) >> 1;
        if (pos <= mid)
            return query(tree[rt].l, pos, cl, mid);
        else
            return query(tree[rt].r, pos, mid + 1, cr);
    }
    void printtree(const int rt)
    {
        for (int i = 1; i <= sz; i++)
        {
            cout << query(rt, i, 1, sz) << " ";
        }
        cout << endl;
    }
    int root[maxn];
};
array<int, 2> vers[maxn];
int n, m;
int ver = 0;
int verfa = 0, versiz = 0;
presistent_array fa, siz; // 开两个数组，直接就是可持久化数组封起来
int getfather(int fart, int x)
{
    int getf = fa.query(fart, x, 1, n);
    if (x == getf)
        return x;
    else
        return getfather(fart, getf);
}
bool same(int fart, int u, int v)
{
    return getfather(fart, u) == getfather(fart, v);
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin >> n >> m;
    fa.sz = siz.sz = n;
    vers[0] = {0, 0};
    for (int i = 1; i <= n; i++)
    {
        fa.update(fa.root[vers[0][0]], i, i, 1, n);
        siz.update(siz.root[vers[0][1]], i, 1, 1, n);
    }
    // fa.printtree(fa.root[0]);
    // siz.printtree(siz.root[0]);
    while (m--)
    {
        ver++;
        vers[ver][0] = vers[ver][1] = ver;
        int op, k;
        cin >> op;
        if (op == 2)
        {
            cin >> k;
            fa.merge(fa.root[vers[ver][0]], fa.root[vers[k][0]], 1, n); // 版本回滚
            siz.merge(siz.root[vers[ver][1]], siz.root[vers[k][1]], 1, n);
        }
        else if (op == 3)
        {
            int u, v;
            cin >> u >> v;
            fa.merge(fa.root[vers[ver][0]], fa.root[vers[ver - 1][0]], 1, n); // 版本复制
            siz.merge(siz.root[vers[ver][1]], siz.root[vers[ver - 1][1]], 1, n);
            cout << same(fa.root[vers[ver][0]], u, v) << endl;
        }
        else
        {
            int u, v;
            cin >> u >> v;
            u = getfather(fa.root[vers[ver - 1][0]], u);
            v = getfather(fa.root[vers[ver - 1][0]], v);
            if (u != v)
            {
                int szu = siz.query(siz.root[vers[ver - 1][1]], u, 1, n);
                int szv = siz.query(siz.root[vers[ver - 1][1]], v, 1, n);
                if (szu < szv)
                {
                    swap(szu, szv);
                    swap(u, v);
                }
                fa.update(fa.root[vers[ver][0]], v, u, 1, n);           // fa[v]=u,小向大合并
                siz.update(siz.root[vers[ver][1]], u, szu + szv, 1, n); // siz[u]+=sizv
            }
            fa.merge(fa.root[vers[ver][0]], fa.root[vers[ver - 1][0]], 1, n); // 先改再复制
            siz.merge(siz.root[vers[ver][1]], siz.root[vers[ver - 1][1]], 1, n);
        }
        // fa.printtree(fa.root[vers[ver][0]]);
        // siz.printtree(siz.root[vers[ver][1]]);
    }
}

1.15 Li-Chao Tree

要求在平面直角坐标系下维护两个操作：

在平面上加入一条线段。记第 $i$ 条被插入的线段的标号为 $i$ 。
给定一个数 $k$ ，询问与直线 $x = k$ 相交的线段中，交点纵坐标最大的线段的编号。

对于 $100\%$ 的数据，保证 $1 \leq n \leq 10^5$ ， $1 \leq k, x_0, x_1 \leq 39989$ ， $1 \leq y_0, y_1 \leq 10^9$ 。

李超树可以优秀的维护平面内添加线性函数线段以及查询 $max{f_i(x)}$ ，可用于斜率优化 $dp$ 等。不支持加入线段后删除，如有必要，考虑线段树分治+李超树实现。

李超树的核心为 $upd$ 函数，更新线段树完整节点区间内的信息。

具体来说，设当前区间的中点为 $mid$ ，我们拿新线段 $f$ 在中点处的值与原最优线段 $g$ 在中点处的值作比较。

如果新线段 $f$ 更优，则将 $f$ 和 $g$ 交换。那么现在考虑在中点处 $f$ 不如 $g$ 优的情况：

若在左端点处 $f$ 更优，那么 $f$ 和 $g$ 必然在左半区间中产生了交点， $f$ 只有在左区间才可能优于 $g$ ，递归到左儿子中进行下传；
若在右端点处 $f$ 更优，那么 $f$ 和 $g$ 必然在右半区间中产生了交点， $f$ 只有在右区间才可能优于 $g$ ，递归到右儿子中进行下传；
若在左右端点处 $g$ 都更优，那么 $f$ 不可能成为答案，不需要继续下传。

除了这两种情况之外，还有一种情况是 $f$ 和 $g$ 刚好交于中点，在程序实现时可以归入中点处 $f$ 不如 $g$ 优的的情况，结果会往 $f$ 更优的一个端点进行递归下传。

最后将 $g$ 作为当前区间的懒标记。

#include <bits/stdc++.h>
using namespace std;
#define i64 long long
#define d64 long double
// #define MOD1 39989
#define MOD1 39989
#define MOD2 1000000000
const int maxn = 2e5 + 5;
struct node
{
    // int l, r;
    int bestcnt;
} tree[maxn << 2LL];
int n, m;
int lastans = 0;
int cnt = 0;
struct segments
{
    // int l, r;
    d64 k, b;
} segs[maxn];
int cmp(d64 x, d64 y)
{
    if (x - y > 1e-9)
        return 1;
    if (y - x > 1e-9)
        return -1;
    return 0;
}
d64 calc(int id, int x)
{
    return segs[id].k * x + segs[id].b;
}
void add(int x0, int y0, int x1, int y1)
{
    cnt++;
    if (x0 == x1)
        segs[cnt].k = 0, segs[cnt].b = max(y0, y1);
    else
        segs[cnt].k = 1.0 * (y1 - y0) / (x1 - x0), segs[cnt].b = y0 - segs[cnt].k * x0;
}
void upd(int now, int rt, int cl, int cr)
{
    int mid = (cl + cr) >> 1LL;
    int &v = tree[rt].bestcnt;
    int bmid = cmp(calc(now, mid), calc(v, mid));
    if (bmid == 1 || (!bmid && now < v))
        swap(now, v);
    int bl = cmp(calc(now, cl), calc(v, cl)), br = cmp(calc(now, cr), calc(v, cr));
    if (bl == 1 || (!bl && now < v))
        upd(now, rt << 1LL, cl, mid);
    if (br == 1 || (!br && now < v))
        upd(now, rt << 1LL | 1LL, mid + 1, cr);
    return;
}
void update(int now, int l, int r, int rt, int cl, int cr)
{
    if (l <= cl && cr <= r)
    {
        upd(now, rt, cl, cr);
        return;
    }
    int mid = (cl + cr) >> 1LL;
    if (l <= mid)
        update(now, l, r, rt << 1LL, cl, mid);
    if (r > mid)
        update(now, l, r, rt << 1LL | 1LL, mid + 1, cr);
    return;
}
pair<double, int> max(pair<double, int> a, pair<double, int> b)
{
    if (cmp(a.first, b.first) == 1)
        return a;
    if (cmp(a.first, b.first) == -1)
        return b;
    return a.second < b.second ? a : b;
}
pair<double, int> query(int d, int rt, int cl, int cr)
{
    if (cr < d || cl > d)
        return {0, 0};
    int mid = (cl + cr) >> 1LL;
    double res = calc(tree[rt].bestcnt, d);
    if (cl == cr)
        return {res, tree[rt].bestcnt};
    return max({res, tree[rt].bestcnt}, max(query(d, rt << 1LL, cl, mid), query(d, rt << 1LL | 1LL, mid + 1, cr)));
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin >> m;
    for (int i = 1; i <= m; i++)
    {
        int opt;
        cin >> opt;
        if (opt == 1)
        {
            int l, r, a, b;
            cin >> l >> a >> r >> b;
            l = (l + lastans - 1) % MOD1 + 1;
            r = (r + lastans - 1) % MOD1 + 1;
            a = (a + lastans - 1) % MOD2 + 1;
            b = (b + lastans - 1) % MOD2 + 1;
            if (l > r)
                swap(l, r), swap(a, b);
            add(l, a, r, b);
            update(cnt, l, r, 1, 1, MOD1);
        }
        else
        {
            int x;
            cin >> x;
            x = (x + lastans - 1) % MOD1 + 1;
            pair<double, int> ans = query(x, 1, 1, MOD1);
            cout << ans.second << endl;
            lastans = ans.second;
        }
    }
    return 0;
}

1.16 类Li-Chao Tree / 递归区间合并

思维，和李超树没有关系，在于两个区间合并pushup的时候比较困难，需要像李超树的upd一样递归处理的情况。

void pushup1(int rt)
{
    tree[rt].maxn = max(tree[rt << 1].maxn, tree[rt << 1 | 1].maxn);
}
int pushup2(d32 tar, int rt, int cl, int cr)
{
    if (tree[rt].maxn <= tar)
        return 0;
    if (a[cl] > tar)
        return tree[rt].len;
    if (cl == cr)
    {
        return (a[cl] > tar);
    }
    int mid = (cl + cr) >> 1;
    if (tree[rt << 1].maxn <= tar)
        return pushup2(tar, rt << 1 | 1, mid + 1, cr);
    return pushup2(tar, rt << 1, cl, mid) + tree[rt].len - tree[rt << 1].len;
}
void pushup(int rt, int cl, int cr)
{
    pushup1(rt);
    int mid = (cl + cr) >> 1;
    tree[rt].len = tree[rt << 1].len + pushup2(tree[rt << 1].maxn, rt << 1 | 1, mid + 1, cr);
}

1.17 线段树分治

假如你需要维护一些信息，这些信息会在某一个时间段内出现，要求在离线的前提下回答某一个时刻的信息并，则可以考虑使用线段树分治的技巧。

实际上线段树分治常有以下用途：

用原本不支持删除但是支持撤销的数据结构来模拟删除操作。如朴素的并查集无法高效支持删边操作。
不同属性的数据分别计算。如需要求出除了某一种颜色外，其他颜色数据的答案。

首先我们建立一个线段树来维护时刻，每一个节点维护一个 vector 来存储位于这一段时刻的信息。

插入一个信息到线段树中和普通线段树的区间修改是类似的。

然后我们考虑如何处理每一个时间段的信息并。考虑从根节点开始分治，维护当前的信息并，然后每到一个节点的时候将这个节点的所有信息进行合并。回溯时撤销这一部分的贡献。最后到达叶子节点时的信息并就是对应的答案。

如果更改信息的时间复杂度为 $O(T(n))$ ，可以通过设置一个栈保留更改，以 $O(T(n))$ 的时间复杂度撤销。撤销不维持均摊复杂度。

整个分治流程的总时间复杂度是 $O(nlogn(T(n)+M(n)))$ 的，其中 $O(M(n))$ 为合并信息的时间复杂度，空间复杂度为 $O(nlogn)$ 。

并查集不嫌麻烦最好写可持久化，不用栈，速度还偏快一点,缺点是码量确实高，而且一旦抄错了不好DEBUG。如果写普通并查集，必须写按秩合并，路径压缩因为均摊复杂度不被支持。撤销时，直接通过栈所记录的merge前的信息直接复原即可。

#define ls (i << 1)
#define rs (i << 1 | 1)
#define mid ((l + r) >> 1)

vector<Object> tree[N << 2];  // 线段树

void update(int ql, int qr, Object obj, int i, int l, int r) {  // 插入
  if (ql <= l && r <= qr) {
    tree[i].push_back(obj);
    return;
  }
  if (ql <= mid) update(ql, qr, obj, ls, l, mid);
  if (qr > mid) update(ql, qr, obj, rs, mid + 1, r);
}

stack<Object> sta;  // 用于撤销的栈
Object now;         // 当前的信息并
Object ans[N];      // 答案

void solve(int i, int l, int r) {
  auto lvl = sta.size();  // 记录一下应当撤销到第几个
  for (Object x : tree[i]) sta.push(now), now = Merge(now, x);  // 合并信息
  if (l == r)
    ans[i] = now;  // 记录一下答案
  else
    solve(ls, l, mid), solve(rs, mid + 1, r);  // 分治
  while (sta.size() != lvl) {                  // 撤销信息
    now = sta.top();
    sta.pop();
  }
}

1.18 线段树维护最大子段和

线段树结点维护区间最值，区间前缀和最值，区间后缀和最值，区间 $op$ 的时候比较一下两个区间的区间最大子段和以及前段后缀+后段前缀的和即可。

#include <bits/stdc++.h>
using namespace std;
#define i64 long long
const int maxn = 5e5 + 9;
struct segtree
{
    struct node
    {
        i64 sum, pre, suf, maxans;
    };
    node tree[maxn << 2];
    i64 a[maxn];
    void pushup(int rt)
    {
        int lson = rt << 1, rson = rt << 1 | 1;
        i64 interval = tree[lson].suf + tree[rson].pre;
        tree[rt].sum = tree[lson].sum + tree[rson].sum;
        tree[rt].pre = max(tree[lson].pre, tree[lson].sum + tree[rson].pre);
        tree[rt].suf = max(tree[rson].suf, tree[rson].sum + tree[lson].suf);
        tree[rt].maxans = max(max(tree[lson].maxans, tree[rson].maxans), interval);
        return;
    }
    void build(int rt, int cl, int cr)
    {
        if (cl == cr)
        {
            tree[rt].sum = tree[rt].pre = tree[rt].suf = tree[rt].maxans = a[cl];
            return;
        }
        int mid = (cl + cr) >> 1;
        build(rt << 1, cl, mid);
        build(rt << 1 | 1, mid + 1, cr);
        pushup(rt);
        return;
    }
    void modify(int pos, int val, int rt, int cl, int cr)
    {
        if (cl == cr)
        {
            tree[rt].sum = tree[rt].pre = tree[rt].suf = tree[rt].maxans = val;
            return;
        }
        int mid = (cl + cr) >> 1;
        if (pos <= mid)
            modify(pos, val, rt << 1, cl, mid);
        else
            modify(pos, val, rt << 1 | 1, mid + 1, cr);
        pushup(rt);
        return;
    }
    node query(int l, int r, int rt, int cl, int cr)
    {
        if (l <= cl && cr <= r)
        {
            return tree[rt];
        }
        int mid = (cl + cr) >> 1;
        if (r <= mid)
            return query(l, r, rt << 1, cl, mid);
        if (l > mid)
            return query(l, r, rt << 1 | 1, mid + 1, cr);
        node lson = query(l, r, rt << 1, cl, mid);
        node rson = query(l, r, rt << 1 | 1, mid + 1, cr);
        node ret;
        i64 interval = lson.suf + rson.pre;
        ret.sum = lson.sum + rson.sum;
        ret.pre = max(lson.pre, lson.sum + rson.pre);
        ret.suf = max(rson.suf, rson.sum + lson.suf);
        ret.maxans = max(max(lson.maxans, rson.maxans), interval);
        return ret;
    }
};
segtree seg;
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        cin >> seg.a[i];
    }
    seg.build(1, 1, n);
    for (int i = 1; i <= m; i++)
    {
        int op, x, y;
        cin >> op >> x >> y;
        if (op == 1)
        {
            if (x > y)
                swap(x, y);
            cout << seg.query(x, y, 1, 1, n).maxans << endl;
        }
        else
        {
            seg.modify(x, y, 1, 1, n);
        }
    }
}

1.19 权值树维护区间有多少个不同的数

$HH$ 的项链，碰到相同的数就把前面那个出现的位置删掉（权值树-1），后面新出现的位置加上（权值树+1）

这玩意儿没求前缀和，不能算主席树。

#include <bits/stdc++.h>
using namespace std;
inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9')
    {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9')
        x = x * 10 + ch - '0', ch = getchar();
    return x * f;
}
void write(int x)
{
    if (x < 0)
        putchar('-'), x = -x;
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
    return;
}
struct Persistant_segtree
{
private:
    struct node
    {
        int l = 0, r = 0;
        int sum = 0;
    };
    vector<node> tree;
    int tot;
    int n;

public:
    Persistant_segtree(int n) : n(n), tot(0)
    {
        tree.assign((n << 5) + 9, node());
    }
    Persistant_segtree() : n(0), tot(0)
    {
        tree.clear();
    }
    void init(int n)
    {
        this->n = n;
        tot = 0;
        tree = vector<node>((n << 5) + 9);
    }
    void update(int &rt1, int rt2, int pos, int val, int cl, int cr)
    {
        if (!rt1)
            rt1 = ++tot;
        tree[rt1].sum = tree[rt2].sum + val;
        if (cl == cr)
        {
            return;
        }
        int mid = (cl + cr) >> 1;
        if (pos <= mid)
            update(tree[rt1].l, tree[rt2].l, pos, val, cl, mid), tree[rt1].r = tree[rt2].r;
        else
            update(tree[rt1].r, tree[rt2].r, pos, val, mid + 1, cr), tree[rt1].l = tree[rt2].l;
    }
    int query(int &rt, int l, int r, int cl, int cr)
    {
        if (!rt)
            return 0;
        if (l <= cl && cr <= r)
            return tree[rt].sum;
        int mid = (cl + cr) >> 1;
        int res = 0;
        if (l <= mid)
            res += query(tree[rt].l, l, r, cl, mid);
        if (r > mid)
            res += query(tree[rt].r, l, r, mid + 1, cr);
        return res;
    }
};
Persistant_segtree pst;
const int maxn = 1e6 + 9;
int a[maxn], lastpos[maxn], root[maxn];
#define endl '\n'
int main()
{
    int n, m;
    n = read();
    pst.init(maxn);
    for (int i = 1; i <= n; i++)
        a[i] = read();
    for (int i = 1; i <= n; i++)
    {
        if (lastpos[a[i]])
        {
            pst.update(root[i], root[i - 1], lastpos[a[i]], -1, 1, n);
            pst.update(root[i], root[i], i, 1, 1, n);
            lastpos[a[i]] = i;
        }
        else
        {
            pst.update(root[i], root[i - 1], i, 1, 1, n);
            lastpos[a[i]] = i;
        }
    }
    m = read();
    while (m--)
    {
        int l, r;
        l = read(), r = read();
        write(pst.query(root[r], l, r, 1, n));
        putchar(endl);
    }
}

1.20 线段树优化建图

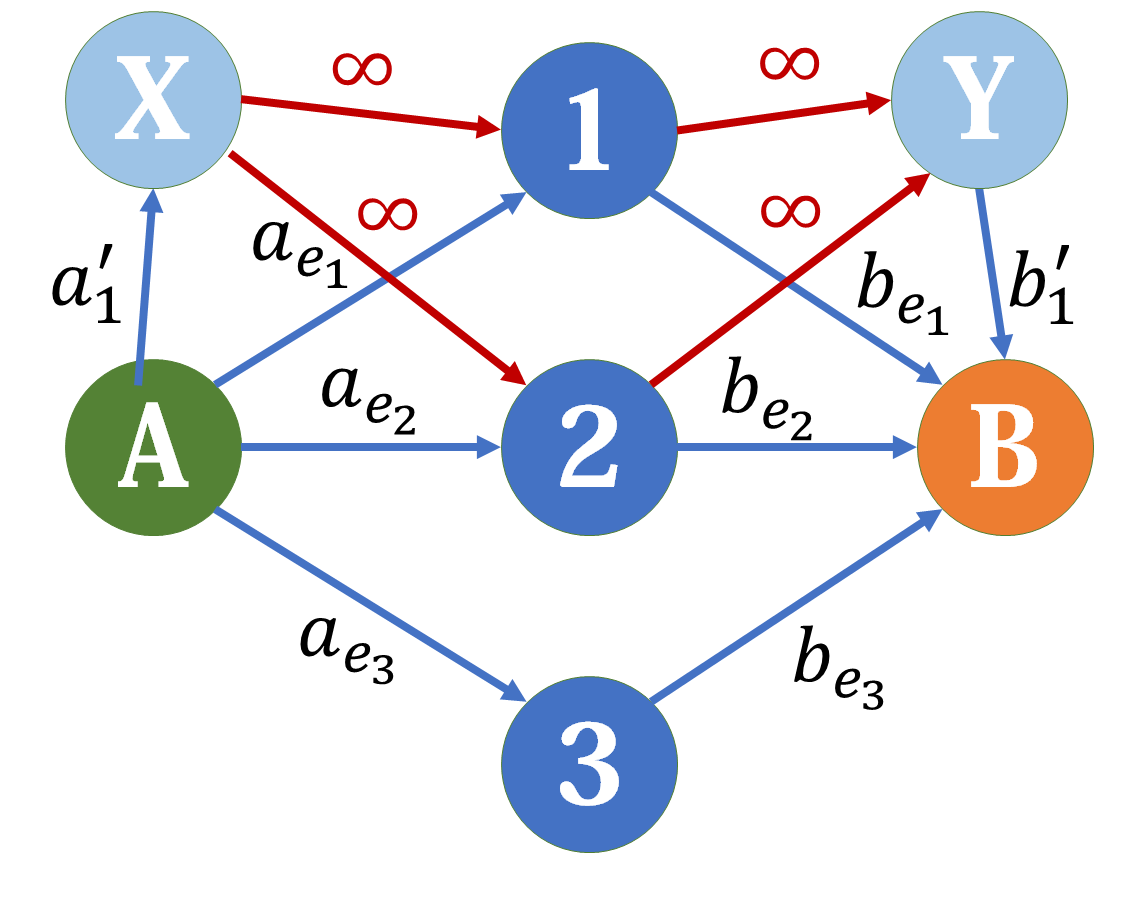
通过线段树区间的性质实现线段树区间连边建图。需要注意的是，从区间连出需要走出树，向区间连入需要走入树，必须保证建立两棵树，出树向根有向边 $(sons\to fa)$ ，入树从根向下有向边 $(fa\to sons)$ ，不可以串行。叶子结点两棵树倒是可以共享，不共享的话叶子结点要做好无向边联通，详情见示例。

有 $n$ 个点、 $q$ 次操作。每一种操作为以下三种类型中的一种:

连一条 $u→v$ 的有向边,权值为 $w$ 。
对于所有 $i∈[l,r]$ 连一条 $u→i$ 的有向边,权值为 $ω$ 。
对于所有 $i∈[l,r]$ 连一条 $i→u$ 的有向边,权值为 $ω$ 。

求从点 $s$ 到其他点的最短路。

$1≤n,q≤10^5,1≤w≤10^9$ 。

// 线段树优化建图
// 区间对区间连边，区间对单点连边，单点对区间连边
// 显然的，需要动态开点线段树，建立的虚点参与跑最短路
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int INF = 1e18;
int tottree = 0, cnt = 0;
int root1 = 0, root2 = 0;
int n;
const int maxn = 4e5 + 9;
int head[maxn << 3LL], to[maxn << 3LL], nxt[maxn << 3LL], w[maxn << 3LL];
int rtnum1[maxn], rtnum2[maxn];
struct node
{
    int l, r;
    int cl, cr;
};
node tree[maxn << 3LL];
void add_edge(int u, int v, int w)
{
    to[++cnt] = v;
    ::w[cnt] = w;
    nxt[cnt] = head[u];
    head[u] = cnt;
}
void build1(int &rt, int cl = 1, int cr = n) // 出树，区间连出
{
    if (!rt)
        rt = ++tottree;
    tree[rt].cl = cl;
    tree[rt].cr = cr;
    if (cl == cr)
    {
        rtnum1[cl] = rt;
        return;
    }
    int mid = (cl + cr) >> 1LL;
    build1(tree[rt].l, cl, mid);
    build1(tree[rt].r, mid + 1, cr);
    add_edge(tree[rt].l, rt, 0);
    add_edge(tree[rt].r, rt, 0);
    return;
}
void build2(int &rt, int cl = 1, int cr = n) // 入树，区间连入
{
    if (!rt)
        rt = ++tottree;
    tree[rt].cl = cl;
    tree[rt].cr = cr;
    if (cl == cr)
    {
        rtnum2[cl] = rt;
        add_edge(rt, rtnum1[cl], 0);
        return;
    }
    int mid = (cl + cr) >> 1LL;
    build2(tree[rt].l, cl, mid);
    build2(tree[rt].r, mid + 1, cr);
    add_edge(rt, tree[rt].l, 0);
    add_edge(rt, tree[rt].r, 0);
    return;
}
void update1(int &rt, int u, int vl, int vr, int w, int cl = 1, int cr = n)
{
    if (!rt)
        return;
    if (vl <= cl && cr <= vr)
    {
        add_edge(rtnum1[u], rt, w);
        return;
    }
    int mid = (cl + cr) >> 1LL;
    if (vl <= mid)
        update1(tree[rt].l, u, vl, vr, w, cl, mid);
    if (vr > mid)
        update1(tree[rt].r, u, vl, vr, w, mid + 1, cr);
}
void update2(int &rt, int v, int ul, int ur, int w, int cl = 1, int cr = n)
{
    if (!rt)
        return;
    if (ul <= cl && cr <= ur)
    {
        add_edge(rt, rtnum2[v], w);
        return;
    }
    int mid = (cl + cr) >> 1LL;
    if (ul <= mid)
        update2(tree[rt].l, v, ul, ur, w, cl, mid);
    if (ur > mid)
        update2(tree[rt].r, v, ul, ur, w, mid + 1, cr);
}
int dist[maxn << 3LL];
bool vis[maxn << 3LL];
void updist(int &rt, int cl = 1, int cr = n)
{
    if (!rt)
        return;
    if (cl == cr)
        return;
    int mid = (cl + cr) >> 1LL;
    dist[tree[rt].l] = min(dist[rt], dist[tree[rt].l]);
    dist[tree[rt].r] = min(dist[rt], dist[tree[rt].r]);
    updist(tree[rt].l, cl, mid);
    updist(tree[rt].r, mid + 1, cr);
    return;
}
void dijkstra(int s)
{
    // memset(dist, 0x3f3f3f3f, sizeof(int) * (tottree + 10));
    for (int i = 1; i <= tottree + 10; i++)
        dist[i] = INF, vis[i] = 0;
    struct qu
    {
        int dis, pos;
        bool operator<(const qu &x) const
        {
            return x.dis < dis;
        }
    };
    priority_queue<qu> q;
    dist[rtnum1[s]] = 0;
    q.push({0, rtnum1[s]});
    while (!q.empty())
    {
        auto [disu, u] = q.top();
        q.pop();
        if (vis[u])
            continue;
        vis[u] = 1;
        for (int i = head[u]; i; i = nxt[i])
        {
            int v = to[i];
            if (dist[v] > dist[u] + w[i])
            {
                dist[v] = dist[u] + w[i];
                q.push({dist[v], v});
            }
        }
    }
    // updist(root);
    return;
}
void clear()
{
    memset(head, 0, sizeof(int) * (tottree + 10));
    cnt = 0, tottree = 0;
    root1 = 0, root2 = 0;
    return;
}
void solve()
{
    int q, s;
    cin >> n >> q >> s;
    build1(root1);
    build2(root2);
    while (q--)
    {
        int op;
        cin >> op;
        int u, v, w, l, r;
        switch (op)
        {
        case 1:
            cin >> u >> v >> w;
            add_edge(rtnum1[u], rtnum2[v], w);
            break;
        case 2:
            cin >> u >> l >> r >> w;
            update1(root2, u, l, r, w);
            break;
        case 3:
            cin >> v >> l >> r >> w;
            update2(root1, v, l, r, w);
            break;
        }
    }
    dijkstra(s);
    for (int i = 1; i <= n; i++)
    {
        if (i == s)
        {
            cout << "0 ";
            continue;
        }
        if (dist[rtnum2[i]] == INF)
            cout << "-1 ";
        else
            cout << dist[rtnum2[i]] << " ";
    }
    cout << endl;
    clear();
    return;
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
    // cin >> t;
    while (t--)
        solve();
    return 0;
}

*1.21 吉司机线段树

线段树维护区间最值操作与区间历史最值的模板。

给出一个长度为 $n$ 的数列 $A$ ，同时定义一个辅助数组 $B$ ， $B$ 开始与 $A$ 完全相同。接下来进行了 $m$ 次操作，操作有五种类型，按以下格式给出：

1 l r k：对于所有的 $i\in[l,r]$ ，将 $A_i$ 加上 $k$ （ $k$ 可以为负数）。
2 l r v：对于所有的 $i\in[l,r]$ ，将 $A_i$ 变成 $\min(A_i,v)$ 。
3 l r：求 $\sum_{i=l}^{r}A_i$ 。
4 l r：对于所有的 $i\in[l,r]$ ，求 $A_i$ 的最大值。
5 l r：对于所有的 $i\in[l,r]$ ，求 $B_i$ 的最大值。

在每一次操作后，我们都进行一次更新，让 $B_i\gets\max(B_i,A_i)$ 。

保证 $1\leq n,m\leq 5\times 10^5$ , $-5\times10^8\leq A_i\leq 5\times10^8$ ,

$op\in[1,5]$ , $1 \leq l\leq r \leq n$ , $-2000\leq k\leq 2000$ ,

$-5\times10^8\leq v\leq 5\times10^8$ 。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
char buf[1<<21],*p1=buf,*p2=buf,obuf[1<<21],*o=obuf;
#define g()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
inline int read()
{
    int s=0,f=1;char c=g();
    for(;!isdigit(c);c=g())
        if(c=='-')f=-1;
    for(;isdigit(c);c=g())
        s=s*10+c-'0';
    return s*f;
}
inline void write(ll x)
{
    static char buf[20];
    static int len=-1;
    if(x<0)putchar('-'),x=-x;
    do buf[++len]=x%10,x/=10;while(x);
    while(len>=0)putchar(buf[len--]+'0');
    putchar('\n');
}
int n,m,op,l,r,k,v;
struct segment_tree{
    ll sum;
    int l,r,maxa,cnt,se,maxb;
    int add1,add2,add3,add4;
}s[2000005];
inline void push_up(int p)
{
    s[p].sum=s[p*2].sum+s[p*2+1].sum;
    s[p].maxa=max(s[p*2].maxa,s[p*2+1].maxa);
    s[p].maxb=max(s[p*2].maxb,s[p*2+1].maxb);
    if(s[p*2].maxa==s[p*2+1].maxa)
    {
        s[p].se=max(s[p*2].se,s[p*2+1].se);
        s[p].cnt=s[p*2].cnt+s[p*2+1].cnt;
    }
    else if(s[p*2].maxa>s[p*2+1].maxa)
    {
        s[p].se=max(s[p*2].se,s[p*2+1].maxa);
        s[p].cnt=s[p*2].cnt;
    }
    else
    {
        s[p].se=max(s[p*2].maxa,s[p*2+1].se);
        s[p].cnt=s[p*2+1].cnt;
    }
}
void build(int l,int r,int p)
{
    s[p].l=l,s[p].r=r;
    if(l==r)
    {
        s[p].sum=s[p].maxa=s[p].maxb=read();
        s[p].cnt=1,s[p].se=-2e9;
        return;
    }
    int mid=(l+r)/2;
    build(l,mid,p*2);
    build(mid+1,r,p*2+1);
    push_up(p);
}
inline void change(int k1,int k2,int k3,int k4,int p)
{
    s[p].sum+=1ll*k1*s[p].cnt+1ll*k2*(s[p].r-s[p].l+1-s[p].cnt);
    s[p].maxb=max(s[p].maxb,s[p].maxa+k3);
    s[p].maxa+=k1;
    if(s[p].se!=-2e9)s[p].se+=k2;
    s[p].add3=max(s[p].add3,s[p].add1+k3);
    s[p].add4=max(s[p].add4,s[p].add2+k4);
    s[p].add1+=k1,s[p].add2+=k2;
}
inline void push_down(int p)
{
    int maxn=max(s[p*2].maxa,s[p*2+1].maxa);
    if(s[p*2].maxa==maxn)
        change(s[p].add1,s[p].add2,s[p].add3,s[p].add4,p*2);
    else change(s[p].add2,s[p].add2,s[p].add4,s[p].add4,p*2);
    if(s[p*2+1].maxa==maxn)
        change(s[p].add1,s[p].add2,s[p].add3,s[p].add4,p*2+1);
    else change(s[p].add2,s[p].add2,s[p].add4,s[p].add4,p*2+1);
    s[p].add1=s[p].add2=s[p].add3=s[p].add4=0;
}
void update_add(int p)
{
    if(l>s[p].r||r<s[p].l)return;
    if(l<=s[p].l&&s[p].r<=r)
    {	
        s[p].sum+=1ll*k*s[p].cnt+1ll*k*(s[p].r-s[p].l+1-s[p].cnt);
        s[p].maxa+=k;
        s[p].maxb=max(s[p].maxb,s[p].maxa);
        if(s[p].se!=-2e9)s[p].se+=k;
        s[p].add1+=k,s[p].add2+=k;
        s[p].add3=max(s[p].add3,s[p].add1);
        s[p].add4=max(s[p].add4,s[p].add2);
        return;
    }
    push_down(p);
    update_add(p*2),update_add(p*2+1);
    push_up(p);
}
void update_min(int p)
{
    if(l>s[p].r||r<s[p].l||v>=s[p].maxa)return;
    if(l<=s[p].l&&s[p].r<=r&&s[p].se<v)
    {
        int k=s[p].maxa-v;
        s[p].sum-=1ll*s[p].cnt*k;
        s[p].maxa=v,s[p].add1-=k;
        return;
    }
    push_down(p);
    update_min(p*2),update_min(p*2+1);
    push_up(p);
}
ll query_sum(int p)
{
    if(l>s[p].r||r<s[p].l)return 0;
    if(l<=s[p].l&&s[p].r<=r)return s[p].sum;
    push_down(p);
    return query_sum(p*2)+query_sum(p*2+1);
}
int query_maxa(int p)
{
    if(l>s[p].r||r<s[p].l)return -2e9;
    if(l<=s[p].l&&s[p].r<=r)return s[p].maxa;
    push_down(p);
    return max(query_maxa(p*2),query_maxa(p*2+1));
}
int query_maxb(int p)
{
    if(l>s[p].r||r<s[p].l)return -2e9;
    if(l<=s[p].l&&s[p].r<=r)return s[p].maxb;
    push_down(p);
    return max(query_maxb(p*2),query_maxb(p*2+1));
}
int main()
{
    n=read(),m=read();
    build(1,n,1);
    while(m--)
    {
        op=read(),l=read(),r=read();
        if(op==1)k=read(),update_add(1);
        else if(op==2)v=read(),update_min(1);
        else if(op==3)write(query_sum(1));
        else if(op==4)printf("%d\n",query_maxa(1));
        else printf("%d\n",query_maxb(1));
    }
    return 0;
}

*1.22 树上数据结构警示（树上线段树）

一般而言，树上数据结构主要是树上权值树以及树上动态开点线段树。这里提及两个需要注意的点

主席树/线段树合并写法的 $merge$ 函数在向父节点合并的时候会有拷贝节点（主席树原理），**如果有多个儿子节点，这种行为会导致父节点信息合并完全之后，子节点的主席树信息被污染。**如果要这么做，涉及到子树信息查询，需要合并dfs的同时进行离线处理，保证污染之后不再查询。

解决方法是树链剖分，尤其是子树信息维护，更是树剖为重中之重。

树上差分不会因为这个受影响的原因在于，树上差分的信息合并是父节点向子节点合并，子节点继承父节点的信息以记录从自己直到根路径上的所有数信息，子节点只有一个父节点可以继承，意味着父节点的信息不会被污染。

（ABC239E 树上子树第 $K$ 大因为这个问题导致WA）
树上合并，一定检查有没有写cl==cr里面的 $\color{red}return$

2.堆(Heap)

关键词：有序序列，只关心最值

2.1 可并堆（左偏树）

定义左偏树中左儿子结点的 $dist_l$ 一定大于等于右儿子节点的 $dist_r$ .

定义某节点 $u$ 的 $dist_u$ 为其到 $u$ 所在子树中最近的外节点（没有左儿子或者右儿子）的距离。

一开始有 $n$ 个小根堆，每个堆包含且仅包含一个数。接下来需要支持两种操作：

1 x y：将第 $x$ 个数和第 $y$ 个数所在的小根堆合并（若第 $x$ 或第 $y$ 个数已经被删除或第 $x$ 和第 $y$ 个数在同一个堆内，则无视此操作）。
2 x：输出第 $x$ 个数所在的堆最小数，并将这个最小数删除（若有多个最小数，优先删除先输入的；若第 $x$ 个数已经被删除，则输出 $-1$ 并无视删除操作）。

注意，这个题需要查某个数在哪个堆，需要并查集，而且因为路径压缩的不成样子，但凡涉及到弹出堆顶，必须连被删除元素一起调整而不是将删除元素简简单单的 fa 归0就可以。

#include <bits/stdc++.h>
using namespace std;
struct heap
{
    int dis, l, r, fa, val;
};
const int maxn = 1e5 + 9;
heap tr[maxn << 5];
int n, m;
int getfather(int x)
{
    return tr[x].fa == x ? x : tr[x].fa = getfather(tr[x].fa);
}
int merge(int x, int y)
{
    if (!x || !y)
        return x | y;
    if (tr[x].val > tr[y].val)
        swap(x, y);
    tr[x].r = merge(tr[x].r, y);
    if (tr[tr[x].l].dis < tr[tr[x].r].dis)
        swap(tr[x].l, tr[x].r);
    tr[x].dis = tr[tr[x].r].dis + 1;
    tr[tr[x].l].fa = tr[tr[x].r].fa = tr[x].fa = x;
    return x;
}
int pop(int x)
{
    tr[x].val = -1;
    tr[tr[x].l].fa = tr[x].l;
    tr[tr[x].r].fa = tr[x].r;
    tr[x].fa = merge(tr[x].l, tr[x].r);
    return 0;
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin >> n >> m;
    for (int i = 1; i <= n; ++i)
        tr[i].fa = i, cin >> tr[i].val;
    int t, x, y;
    for (int i = 1; i <= m; ++i)
    {
        cin >> t >> x;
        if (t == 1)
        {
            cin >> y;
            if (tr[x].val == -1 || tr[y].val == -1)
                continue;
            int l = getfather(x), r = getfather(y);
            if (l != r)
                tr[l].fa = tr[r].fa = merge(l, r);
        }
        else
        {
            if (tr[x].val == -1)
                cout << -1 << endl;
            else
                cout << tr[getfather(x)].val << endl, pop(getfather(x));
        }
    }
    return 0;
}

2.2 带懒标记左偏树

像动态开点线段树一样，合并时注意标记下传问题

struct node
{
    int dis, val; int ch[2]; int fa; int lazyadd = 0, lazymul = 1;
    int id; int cnt; int lazyc = 0;
};
int &rs(int rt) {return tree[rt].ch[tree[tree[rt].ch[0]].dis > tree[tree[rt].ch[1]].dis];/*注意rs写法*/}
int &ls(int rt) {return tree[rt].ch[1 ^ (tree[tree[rt].ch[0]].dis > tree[tree[rt].ch[1]].dis)];/*更注意ls写法*/}
int &dis(int rt) {return tree[rt].dis;}
int &val(int rt) {return tree[rt].val;}
int &fa(int rt) {return tree[rt].fa;}
int &lazyadd(int rt) {return tree[rt].lazyadd;}
int &lazymul(int rt) {return tree[rt].lazymul;}
int &lazyc(int rt) {return tree[rt].lazyc;}
int &vcnt(int rt) {return tree[rt].cnt;}
int &id(int rt) {return tree[rt].id;}
void pushdown(int rt)
{
    if (!rt)
        return;
    if (lazyadd(rt) != 0 || lazymul(rt) != 1 || lazyc(rt) != 0)
    {
        if (ls(rt))
        {
            val(ls(rt)) = val(ls(rt)) * lazymul(rt) + lazyadd(rt);
            vcnt(ls(rt)) += lazyc(rt);
            lazymul(ls(rt)) *= lazymul(rt);
            lazyadd(ls(rt)) = lazyadd(ls(rt)) * lazymul(rt) + lazyadd(rt);
            lazyc(ls(rt)) += lazyc(rt);
        }
        if (rs(rt))
        {
            val(rs(rt)) = val(rs(rt)) * lazymul(rt) + lazyadd(rt);
            vcnt(rs(rt)) += lazyc(rt);
            lazymul(rs(rt)) *= lazymul(rt);
            lazyadd(rs(rt)) = lazyadd(rs(rt)) * lazymul(rt) + lazyadd(rt);
            lazyc(rs(rt)) += lazyc(rt);
        }
        lazyadd(rt) = 0;
        lazymul(rt) = 1;
        lazyc(rt) = 0;
    }
    return;
}
int merge(int rt1, int rt2)
{
    if (!rt1 || !rt2)
        return rt1 | rt2;
    if (val(rt1) > val(rt2))
        swap(rt1, rt2);
    pushdown(rt1);
    int &r = rs(rt1);
    r = merge(r, rt2);
    fa(r) = rt1;
    dis(rt1) = dis(rs(rt1)) + 1; // 严禁使用pushup于此，pushup只用于删除任意非根节点时使用，删除根节点要pop
    return rt1;
}
int pop(int rt1)
{
    pushdown(rt1);
    return merge(ls(rt1), rs(rt1));
}
int tot = 0;
int push(int rt1, int val, int id)
{
    tree[++tot].val = val;
    tree[tot].id = id;
    return merge(rt1, tot);
}

*2.3 支持删除任意节点可并堆

没有专门的题，有涉及到可并堆删对应节点的理论上主席树都可以做，而且复杂度是一样的，优先写自己顺手的。

这里是OI-wiki的

void erase(int x) {
  int y = merge(ls(x), rs(x));
  fa(y) = fa(x);
  if (ls(fa(x)) == x)
    ls(fa(x)) = y;
  else if (rs(fa(x)) == x)
    rs(fa(x)) = y;
  pushup(fa(y));
}

*2.4 GNU/GCC pb_ds库

pb_ds库提供了五种可并堆，默认大根堆，greater标签使用和普通 $STL$ 一致。

#include<ext/pb_ds/priority_queue.hpp>
using namespace __gnu_pbds;
__gnu_pbds::priority_queue<int>q;//因为放置和std重复，故需要带上命名空间
__gnu_pbds::priority_queue<int,greater<int>,pairing_heap_tag> q;//最快
__gnu_pbds::priority_queue<int,greater<int>,binary_heap_tag> q;
__gnu_pbds::priority_queue<int,greater<int>,binomial_heap_tag> q;
__gnu_pbds::priority_queue<int,greater<int>,rc_binomial_heap_tag> q;
__gnu_pbds::priority_queue<int,greater<int>,thin_heap_tag> q;
__gnu_pbds::priority_queue<int,greater<int> > q;

pairing_heap_tag : push和join为 $O(1)$ ,其余为均摊 $O(logn)$ 。

binary_heap_tag:只支持push和pop,均为均摊 $O(logn)$ 。

binomial_heap_tag:push为均摊 $O(1)$ ,其余为 $O(logn)$ 。

rc_binomial_heap_tag: push为 $O(1)$ ,其余为 $O(logn)$ 。

thin_heap_tag: push为 $O(1)$ ,不支持join,其余为 $O(logn)$ ;但是如果只有increase_key,那么modify为均摊 $O(1)$ 。“不支持”不是不能用,而是用起来很慢

操作表：

size()用法同std
empty()用法同std
push(const_reference r_val)注意push返回point_iterator，被push元素入堆后位置
top()没区别…
pop()弹出堆顶
point_iterator对应某元素的迭代器
erase(point_iterator it)删除对应点
modify(point_iterator it,const_reference r_new_val)修改对应点的值

这是优化 $dijkstra$ 神方法,均摊复杂度 $O(1)$

优化 $dijkstra$ 的思路就是在前面提到的 $std$ 优先队列优化的基础上,维护一个point_iterator数组,push的时候存下push时返回的迭代器,更新dis是判断是否存在此迭代器,若存在 $O(1)$ modify,不存在均摊 $O(1)$ push
clear()基本没什么用,还不如重新定义一个…
join(priority_queue &other)可并堆啊,还是 $O(1)$ 的,注意合并后other会被清空
其他迭代器同std

使用示例：

#include <bits/stdc++.h>
#include <ext/pb_ds/priority_queue.hpp>
using namespace std;
#define int long long
using mergeable_priority_queue = __gnu_pbds::priority_queue<int, less<int>, __gnu_pbds::pairing_heap_tag>;
const int maxn = 2e5 + 9;
int ans = 0;
vector<int> connects[maxn];
mergeable_priority_queue qs[maxn];
int sum[maxn];
int L[maxn];
int n, m;
void dfs(int u, int fa)
{
    for (auto v : connects[u])
    {
        if (v == fa)
            continue;
        dfs(v, u);
        qs[u].join(qs[v]);
        sum[u] += sum[v];
    }
    while (!qs[u].empty() && sum[u] > m)
    {
        sum[u] -= qs[u].top();
        qs[u].pop();
    }
    ans = max(ans, (int)(qs[u].size()) * L[u]);
    return;
}
signed main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        int fa, c, l;
        cin >> fa >> c >> l;
        qs[i].push(c);
        sum[i] += c, L[i] = l;
        connects[fa].push_back(i);
        connects[i].push_back(fa);
    }
    dfs(0, 0);
    cout << ans << endl;
}

3.ST表（Sparse Table）

关键词：静态区间，可重复贡献

稀疏表，倍增，可以解决可重复贡献问题：

代数系统 $<S,\cdot >$ 满足以下条件：

该代数系统为半群。
对于 $\forall x\in S,x\cdot x=x$ （可重复贡献）

除 RMQ 以外，还有其它的「可重复贡献问题」。例如「区间按位与」、「区间按位或」、「区间 GCD」，ST 表都能高效地解决。

如果碰到恶心的卡内存的，考虑ST表存对应答案在原数组的下标，节省空间。

3.1 静态区间最值，一维ST表

// ST表，静态区间最大值
#include <bits/stdc++.h>
using namespace std;
int getlog(int n)
{
    int ans = 0;
    while (n)
    {
        n >>= 1;
        ans++;
    }
    return ans - 1;
}
const int maxn = 5e5 + 10;
int st[maxn][20];
#define endl '\n'
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin >> n;
    int q;
    cin >> q;
    int logn = getlog(n);
    for (int i = 1; i <= n; i++)
    {
        cin >> st[i][0];
    }
    for (int j = 1; j <= logn; j++)
    {
        for (int i = 1; i + (1 << j) - 1 <= n; i++)
        {
            st[i][j] = max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
        }
    }
    while (q--)
    {
        int l, r;
        cin >> l >> r;
        int dis = r - l + 1;
        int k = getlog(dis);
        cout << max(st[l][k], st[r - (1 << k) + 1][k]) << endl;
    }
}

3.2 静态区间最值，二维ST表

类比一维 $ST$ 表，我们定义数组 $st[i][j][k][p]$ 表示从 $(i,j)$ 往下 $2^k$ 个元素，往右 $2^p$ 个元素的最值。

建表的话，同样类比一维 $ST$ 表，外层两个循环 $k$ 和 $p$ , 然后内层取最值就行了。要注意的是， $k$ 和 $p$ 要从 $0$ 开始循环，因为一行或者一列的情况也要维护。

复杂度 $O(n^2log^2n)$

void build_st()
{
    for (int i = 0; i < 9; i++)
    {
        for (int j = 0; j < 9; j++)
        {
            if (i == 0 && j == 0)
                continue;
            for (int k = 1; k <= n - (1 << i) + 1; k++)
            {
                for (int p = 1; p <= n - (1 << j) + 1; p++)
                {
                    if (i == 0)
                        st[k][p][i][j] = min(st[k][p][i][j - 1], st[k][p + (1 << j - 1)][i][j - 1]);
                    else
                        st[k][p][i][j] = min(st[k][p][i - 1][j], st[k + (1 << i - 1)][p][i - 1][j]);
                }
            }
        }
    }
}

int query(int r1, int c1, int r2, int c2)
{
    int k1 = log2(r2 - r1 + 1);
    int k2 = log2(c2 - c1 + 1);
    return min(st[r1][c1][k1][k2], min(st[r2 - (1 << k1) + 1][c1][k1][k2], min(st[r1][c2 - (1 << k2) + 1][k1][k2], st[r2 - (1 << k1) + 1][c2 - (1 << k2) + 1][k1][k2])));
}

3.3 倍增ST表求解LCA问题

倍增优化求 $LCA$ ， $dfs$ 预处理祖先信息，然后查询时先跳到同一高度，再一起暴力向上跳。暴力向上跳必须从大向小枚举。预处理 $O(nlogn)$ ，单次查询 $O(n)$ .

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 9;
vector<int> connects[maxn];
int fa[maxn][21];
int dep[maxn];
inline void dfs(int u, int fas)
{
    dep[u] = dep[fas] + 1;
    fa[u][0] = fas;
    for (int j = 1; j <= 20; j++)
    {
        fa[u][j] = fa[fa[u][j - 1]][j - 1];
    }
    for (auto v : connects[u])
    {
        if (v == fas)
            continue;
        dfs(v, u);
    }
    return;
}
inline int lca(int u, int v)
{
    if (dep[u] < dep[v])
        swap(u, v);
    int tmp = dep[u] - dep[v];
    for (int j = 0; j <= 20; j++)
    {
        if ((tmp >> j) & 1)
            u = fa[u][j];
    }
    if (u == v)
        return u;
    for (int j = 20; j >= 0; j--)
    {		
        if (fa[u][j] != fa[v][j])
        {
            u = fa[u][j], v = fa[v][j];
        }
    }
    return fa[u][0];
}
int main()
{
    int n, m, rt;
    cin >> n >> m >> rt;
    for (int i = 1; i < n; i++)
    {
        int u, v;
        cin >> u >> v;
        connects[u].push_back(v);
        connects[v].push_back(u);
    }
    dfs(rt, rt);
    while (m--)
    {
        int u, v;
        cin >> u >> v;
        cout << lca(u, v) << endl;
    }
    return 0;
}

3.4 欧拉序ST表求LCA问题

问题转化成 $dfs$ 遍历路径记录下结点的 $dfn$ 序号上 $RMQ$ 问题，两个节点的 $lca$ 一定是欧拉序遍历下序号区间内深度最浅的结点。可以做到 $O(nlogn)$ 预处理，单次询问 $O(1)$ .

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e6 + 9;
vector<int> connects[maxn];
int st[maxn << 1][25];
int dep[maxn];
int pos[maxn];
int logs[maxn << 1];
void add_edge(int u, int v)
{
    connects[u].push_back(v);
    connects[v].push_back(u);
}
int cnt = 0;
void dfs1(int u, int fa)
{
    st[++cnt][0] = u;
    dep[u] = dep[fa] + 1;
    pos[u] = cnt;
    for (auto v : connects[u])
    {
        if (v == fa)
            continue;
        dfs1(v, u);
        st[++cnt][0] = u;//欧拉序记录
    }
    return;
}
void build_st()
{
    for (int j = 1; j < 25; j++)
        for (int i = 1; i + (1 << j) - 1 <= cnt; i++)
        {
            int l = st[i][j - 1], r = st[i + (1 << (j - 1))][j - 1];//st维护结点序号
            if (dep[l] < dep[r])
                st[i][j] = l;
            else
                st[i][j] = r;
        }
    logs[1] = 0;
    for (int i = 2; i <= cnt; i++)
    {
        logs[i] = logs[i / 2] + 1;
    }
    return;
}
int lcas(int u, int v)
{
    int l = pos[u], r = pos[v];
    if (l > r)
        swap(l, r);
    int k = logs[r - l + 1];
    int ansl = st[l][k];
    int ansr = st[r - (1 << k) + 1][k];
    if (dep[ansl] < dep[ansr])
        return ansl;
    else
        return ansr;
}
int main()
{
    int n, m, rt;
    cin >> n >> m >> rt;
    for (int i = 1; i < n; i++)
    {
        int u, v;
        cin >> u >> v;
        add_edge(u, v);
    }
    dfs1(rt, rt);
    build_st();
    while (m--)
    {
        int u, v;
        cin >> u >> v;
        cout << lcas(u, v) << endl;
    }
    return 0;
}

4.并查集(Disjoint Sets)

关键词：同属性分类

4.1 带权并查集

维护路径权值信息，常见用路径压缩均摊复杂度。merge时搞不清就画向量图表示，一下就懂。

int getfather(int x)
{
    int fa = father[x];
    if (x != father[x])
    {
        father[x] = getfather(father[x]);
        val[x] += val[fa];
        return father[x];
    }
    return x;
}
void merge(int x, int y, int value)
{
    int fx = getfather(x);
    int fy = getfather(y);
    father[fx] = fy;
    val[fx] = value + val[y] - val[x];
}

4.2 种类并查集

一个点拆成多个点维护对立矛盾等信息。

#include <iostream>
#include <cstdlib>
using namespace std;
const int maxn = 1e6 + 1;
int father[maxn];
int ran[maxn];
int n;
int getfather(int x)
{
    if (x == father[x])
        return x;
    return father[x] = getfather(father[x]);
}
void merge(int x, int y)
{
    int fx = getfather(x);
    int fy = getfather(y);
    father[fx]=fy;
}
void eat(int x, int y)
{
    merge(x, n + y);
    merge(n + x, 2 * n + y);
    merge(2 * n + x, y);
}
void same(int x, int y)
{
    merge(x, y);
    merge(n + x, n + y);
    merge(2 * n + x, 2 * n + y);
}
bool checkeat(int x, int y)
{
    return getfather(x) == getfather(y + n) || getfather(x) == getfather(y + 2 * n); // 查询捕食和被捕食关系
}
bool checksame(int x, int y)
{
    return (getfather(x) == getfather(y)) || x == y;
}
void init(int n)
{
    for (int i = 1; i <= 3 * n; i++)
    {
        father[i] = i;
    }
}

4.3 可持久化并查集

见1.14

5.树状数组(Fenwick Trees)

关键词：二进制枚举，前缀和

树状数组维护类似前缀和的东西。核心操作为lowbit。

5.1 二维树状数组（模板，子矩形所有元素和）

一维的树状数组都会写。下面的是二维的。维护矩形前缀和

// 高位树状数组，没啥大区别，开多个
#include <bits/stdc++.h>
using namespace std;
#define i64 int
struct Fenwick
{
private:
    int n, m;
    vector<vector<i64>> c;
    int lowbit(int x) { return x & -x; }

public:
    Fenwick(int n, int m) : n(n), m(m), c(n + 1, vector<i64>(m + 1, 0)) {}
    Fenwick() : n(0), m(0) {}
    void init(int n, int m)
    {
        this->n = n;
        this->m = m;
        c.assign(n + 1, vector<i64>(m + 1, 0));
    }
    void add(int x, int y, i64 v)
    {
        for (int i = x; i <= n; i += lowbit(i))
            for (int j = y; j <= m; j += lowbit(j))
                c[i][j] += v;
    }
    i64 query(int x, int y)
    {
        i64 res = 0;
        for (int i = x; i; i -= lowbit(i))
            for (int j = y; j; j -= lowbit(j))
                res += c[i][j];
        return res;
    }
};

5.2 离线二维数点

求 $[l,r]$ 内小于等于 $x$ 的点有多少个。

// 离线二维数点，扫描线离线版本
#include <bits/stdc++.h>
using namespace std;
#define i64 int
struct Fenwick
{
private:
    int _n;
    vector<i64> c;

public:
    void init(int n)
    {
        _n = n;
        c = vector<i64>(n + 1, 0);
    }
    void add(int x, i64 d)
    {
        for (; x <= _n; x += (x & -x))
            c[x] += d;
    }
    i64 query(int x)
    {
        i64 res = 0;
        for (; x; x -= (x & -x))
            res += c[x];
        return res;
    }
};
Fenwick fw;
const int maxn = 2e6 + 10;
vector<pair<int, int>> mp[maxn];
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int n, q;
    cin >> n >> q;
    vector<int> a(n + 1);
    int maxs = 0;
    for (int i = 1; i <= n; i++)
        cin >> a[i], maxs = max(maxs, a[i]);
    vector<tuple<int, int, int>> query(q + 1);
    vector<int> ans(q + 1);
    for (int i = 1; i <= q; i++)
    {
        int l, r, x;
        cin >> l >> r >> x;
        query[i] = {l, r, x};
        mp[r].push_back({i, 1});
        mp[l - 1].push_back({i, -1});
    }
    fw.init(maxs + 100);
    for (int i = 1; i <= n; i++)
    {
        fw.add(a[i], 1);
        for (auto &j : mp[i])
        {
            ans[j.first] += j.second * fw.query(get<2>(query[j.first]));
        }
    }
    for (int i = 1; i <= q; i++)
        cout << ans[i] << '\n';
    return 0;
}

6.平衡树（Bindary Search AVL Tree）

关键词：有序序列，动态插入与删除。

6.1 普通平衡树

说实话，裸平衡树用的真不多，能用 $set$ 、 $multiset$ 等 $STL$ 实现的东西为啥要自己写。

更新：需要知道排名就别尼玛想你的multiset了，赶紧给我滚去写 $Treap$ !

平衡树可提供以下操作：

插入一个数 $x$ 。
删除一个数 $x$ （若有多个相同的数，应只删除一个）。
定义排名为比当前数小的数的个数 $+1$ 。查询 $x$ 的排名。
查询数据结构中排名为 $x$ 的数。
求 $x$ 的前驱（前驱定义为小于 $x$ ，且最大的数）。
求 $x$ 的后继（后继定义为大于 $x$ ，且最小的数）。

对于操作 3,5,6，不保证当前数据结构中存在数 $x$ ， $1\le n \le 10^5$ .

6.1.1 替罪羊树（ScapeGoat Tree）

替罪羊树是一个很暴力的思想，每次插入一个数动态检查插入后某些节点是否需要暴力进行平衡重构。一般选择平衡因子 $\alpha=0.7-0.8$ 。如果某个子树的左儿子所管辖子树大小占比例超过平衡因子就重构。重构就是中序遍历暴力重构即可。

复杂度均摊 $O(nlogn)$ ，树高均摊 $O(logn)$

下面示例中，重复点算作新开点，点总数不得超过 $1e5$ 级别。平衡树构建时，默认左儿子权值必须严格小于自身，即相同权值结点必定是全部挂载于右儿子上。

#include <bits/stdc++.h>
using namespace std;
const int inf = (1 << 30);
typedef long long ll;
const int maxn = 1e6 + 5;
vector<int> vec;
struct node
{
    int ls, rs, w; // 左儿子，有儿子，节点权值
    bool exist;    // 该节点所代表元素是否存在
    int sizx;      // 该节点下属子树大小
    int fact;      // 该节点下属子树中尚存在元素个数
} tr[maxn];
int cnt, root;
void pushup(int now) // 维护节点信息
{
    tr[now].sizx = tr[tr[now].ls].sizx + tr[tr[now].rs].sizx + 1;
    tr[now].fact = tr[tr[now].ls].fact + tr[tr[now].rs].fact + 1;
}
void newnode(int &now, int w) // 开新点
{
    now = ++cnt;
    tr[now].w = w, tr[now].sizx = tr[now].fact = 1;
    tr[now].exist = true;
}
bool judge(int now) // 判断是否平衡
{
    if (max(tr[tr[now].ls].sizx, tr[tr[now].rs].sizx) > tr[now].sizx * 0.75)
        return true;
    if ((tr[now].sizx - tr[now].fact) > tr[now].sizx * 0.3)
        return true;
    return false;
}
void mds(int now) // 中序遍历
{
    if (!now)
        return;
    mds(tr[now].ls);
    if (tr[now].exist)
        vec.push_back(now);
    mds(tr[now].rs);
}
void cre(int L, int R, int &now) // 构造标准平衡树
{
    if (L == R)
    {
        now = vec[L];
        tr[now].ls = tr[now].rs = 0;
        tr[now].sizx = tr[now].fact = 1;
        return;
    }
    int mid = (L + R) >> 1;
    while (L < mid && tr[vec[mid]].w == tr[vec[mid - 1]].w)
        mid--;
    now = vec[mid];
    if (L < mid)
        cre(L, mid - 1, tr[now].ls);
    else
        tr[now].ls = 0;
    cre(mid + 1, R, tr[now].rs);
    pushup(now);
}
void update(int now, int en) // 维护父辈节点
{
    if (!now)
        return;
    if (tr[now].w > tr[en].w)
        update(tr[now].ls, en);
    else
        update(tr[now].rs, en);
    tr[now].sizx = tr[tr[now].ls].sizx + tr[tr[now].rs].sizx + 1;
}
void rebuild(int &now) // 重构树
{
    vec.clear();
    mds(now);
    if (vec.empty())
    {
        now = 0;
        return;
    }
    cre(0, vec.size() - 1, now);
}
void check(int &now, int en) // 检查，并重构子树
{
    if (now == en)
        return;
    if (judge(now))
    {
        rebuild(now);
        update(root, now);
        return;
    }
    if (tr[en].w < tr[now].w)
        check(tr[now].ls, en);
    else
        check(tr[now].rs, en);
}
void inser(int &now, int w) // 插入
{
    if (!now)
    {
        newnode(now, w);
        check(root, now);
        return;
    }
    tr[now].sizx++, tr[now].fact++;
    if (w < tr[now].w)
        inser(tr[now].ls, w);
    else
        inser(tr[now].rs, w);
}
void del(int now, int w) // 删除
{
    if (tr[now].exist && tr[now].w == w)
    {
        tr[now].exist = false;
        tr[now].fact--;
        check(root, now);
        return;
    }
    tr[now].fact--;
    if (w < tr[now].w)
        del(tr[now].ls, w);
    else
        del(tr[now].rs, w);
}
int getrank(int w) // 求w的排名
{
    int now = root, rank = 1;
    while (now)
    {
        if (w <= tr[now].w)
            now = tr[now].ls;
        else
        {
            rank += tr[now].exist + tr[tr[now].ls].fact, now = tr[now].rs;
        }
    }
    return rank;
}
int getnum(int rank) // 求排名为rank的树数
{
    int now = root;
    while (now)
    {
        if (tr[now].exist && tr[tr[now].ls].fact + tr[now].exist == rank)
            break;
        else if (rank <= tr[tr[now].ls].fact)
            now = tr[now].ls;
        else
        {
            rank -= tr[now].exist + tr[tr[now].ls].fact, now = tr[now].rs;
        }
    }
    return tr[now].w;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int n;
    cin >> n;
    while (n--)
    {
        int op, x;
        cin >> op >> x;
        switch (op)
        {
        case 1:
            inser(root, x);
            break;
        case 2:
            del(root, x);
            break;
        case 3:
            cout << getrank(x) << endl;
            break;
        case 4:
            cout << getnum(x) << endl;
            break;
        case 5:
            cout << getnum(getrank(x) - 1) << endl;
            break;
        case 6:

            cout << getnum(getrank(x + 1)) << endl;
            break;
        }
    }
}

6.1.2 树堆（Treap）

$Treap=Tree+Heap$ ，是一种弱平衡性质的平衡树，均摊树深度 $O(logn)$ 。

每一个树节点多赋值一个随机权值，使得该树既满足平衡树性质（ $val_{lson}<val_{rt}< val_{rson}$ ），又满足堆的性质（ $w_{lson}<w_{rt},w_{rt}>w_{rson}$ ）

复杂度正确性由随机数保证。

关于更多的Treap，详见6.2 笛卡尔树

此处的示例因题目保证前驱后继必定存在故没有特判，如果前驱后继不存在对应函数必定卡死，解决方案参见6.3.1可持久化Treap中的解决方式。

6.1.2.1 有旋Treap

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 100005;
const int inf = 0x3f3f3f3f;
unsigned int seed;
random_device rd;
mt19937 ran;
struct Treap
{
    struct node
    {
        int val, rnd, lc, rc, size, num;
    };
    int cnt = 0;
    node tr[MAXN];
    void init()
    {
        cnt = 0;
    }
    int _rand()
    {
        ran.seed(rd());
        return ran();
    }
    void pushup(int p)
    {
        tr[p].size = tr[tr[p].lc].size + tr[tr[p].rc].size + tr[p].num;
    }
    void right(int &k)
    {
        int tmp = tr[k].lc;
        tr[k].lc = tr[tmp].rc;
        tr[tmp].rc = k;
        tr[tmp].size = tr[k].size;
        pushup(k);
        k = tmp;
    }
    void left(int &k)
    {
        int tmp = tr[k].rc;
        tr[k].rc = tr[tmp].lc;
        tr[tmp].lc = k;
        tr[tmp].size = tr[k].size;
        pushup(k);
        k = tmp;
    }
    void insert(int &p, int x)
    {
        if (p == 0)
        {
            p = ++cnt;
            tr[p].val = x;
            tr[p].num = tr[p].size = 1;
            tr[p].lc = tr[p].rc = 0;
            tr[p].rnd = _rand();
            return;
        }
        ++tr[p].size;
        if (x == tr[p].val)
            ++tr[p].num;
        else if (x < tr[p].val)
        {
            insert(tr[p].lc, x);
            if (tr[tr[p].lc].rnd < tr[p].rnd)
                right(p);
        }
        else if (x > tr[p].val)
        {
            insert(tr[p].rc, x);
            if (tr[tr[p].rc].rnd < tr[p].rnd)
                left(p);
        }
    }
    void del(int &p, int x)
    {
        if (p == 0)
            return;
        if (tr[p].val == x)
        {
            if (tr[p].num > 1)
                --tr[p].num, --tr[p].size;
            else
            {
                if (tr[p].lc == 0 || tr[p].rc == 0)
                    p = tr[p].lc + tr[p].rc;
                else if (tr[tr[p].lc].rnd < tr[tr[p].rc].rnd)
                    right(p), del(p, x);
                else if (tr[tr[p].lc].rnd > tr[tr[p].rc].rnd)
                    left(p), del(p, x);
            }
        }
        else if (tr[p].val < x)
            --tr[p].size, del(tr[p].rc, x);
        else
            --tr[p].size, del(tr[p].lc, x);
    }
    int queryrnk(int &p, int x)
    {
        if (p == 0)
            return 0;
        else if (tr[p].val == x)
            return tr[tr[p].lc].size;
        else if (tr[p].val < x)
            return tr[tr[p].lc].size + tr[p].num + queryrnk(tr[p].rc, x);
        else
            return queryrnk(tr[p].lc, x);
    }
    int querynum(int &p, int rnk)
    {
        if (p == 0)
            return 0;
        if (tr[tr[p].lc].size >= rnk)
            return querynum(tr[p].lc, rnk);
        rnk -= tr[tr[p].lc].size;
        if (rnk <= tr[p].num)
            return tr[p].val;
        rnk -= tr[p].num;
        return querynum(tr[p].rc, rnk);
    }
    int queryfront(int &p, int x)
    {
        if (p == 0)
            return -inf;
        if (tr[p].val < x)
            return max(tr[p].val, queryfront(tr[p].rc, x));
        else if (tr[p].val >= x)
            return queryfront(tr[p].lc, x);
    }
    int queryback(int &p, int x)
    {
        if (p == 0)
            return inf;
        if (tr[p].val > x)
            return min(tr[p].val, queryback(tr[p].lc, x));
        else if (tr[p].val <= x)
            return queryback(tr[p].rc, x);
    }
};
int pos;
Treap tr;
int main()
{
    int n;
    scanf("%d", &n);
    int m, k;
    tr.init();
    for (int i = 0; i < n; ++i)
    {
        scanf("%d%d", &m, &k);
        if (m == 1)
            tr.insert(pos, k);
        else if (m == 2)
            tr.del(pos, k);
        else if (m == 3)
            printf("%d\n", tr.queryrnk(pos, k) + 1);
        else if (m == 4)
            printf("%d\n", tr.querynum(pos, k));
        else if (m == 5)
            printf("%d\n", tr.queryfront(pos, k));
        else if (m == 6)
            printf("%d\n", tr.queryback(pos, k));
    }
    return 0;
}

6.1.2.2 无旋Treap（FHQ-Treap)

无旋转 $Treap$ 通过树分裂和合并实现节点的添加以及删除。可以支持固定区间操作，支持可持久化操作。

6.1.2.2.1 单个节点只有一个值，相同值使用多个节点，可支持split_sz

#include <bits/stdc++.h>
using namespace std;
random_device rd;
mt19937 ran(rd());
struct Treap
{
    struct node
    {
        int l, r;
        int w;
        int val;
        int sz;
        node() : l(0), r(0), w(0), val(0), sz(0) {};
        node(int val) : l(0), r(0), w(ran()), val(val), sz(1) {};
    };
    const static int maxn = 5e5 + 9;
    node tree[maxn];
    int root;
    int tot = 0;
    int newnode(int val)
    {
        tot++;
        tree[tot] = node(val);
        return tot;
    }
    inline void pushup(int rt)
    {
        tree[rt].sz = tree[tree[rt].l].sz + tree[tree[rt].r].sz + 1;
        return;
    }
    inline void split_val(const int rt, int &l, int &r, int val)
    {
        if (!rt)
        {
            l = r = 0;
            return;
        }
        if (tree[rt].val <= val) // 叶子权值比目标值小，必定属于左侧。
        {
            l = rt;
            split_val(tree[rt].r, tree[rt].r, r, val);
        }
        else
        {
            r = rt;
            split_val(tree[rt].l, l, tree[rt].l, val);
        }
        pushup(rt);
    }
    inline void split_sz(const int rt, int &l, int &r, int sz)
    {
        if (!rt)
        {
            l = r = 0;
            return;
        }
        if (tree[tree[rt].l].sz + 1 <= sz)
        {
            l = rt;
            split_sz(tree[rt].r, tree[rt].r, r, sz - (tree[tree[rt].l].sz + 1));
        }
        else
        {
            r = rt;
            split_sz(tree[rt].l, l, tree[rt].l, sz);
        }
        pushup(rt);
    }
    inline void merge(int &rt, const int l, const int r)
    {
        if (!l || !r)
        {
            rt = l | r;
            return;
        }
        if (tree[l].w > tree[r].w) // 大根堆形式，小根堆换个号就行
        {
            rt = l;
            merge(tree[rt].r, tree[rt].r, r);
        }
        else
        {
            rt = r;
            merge(tree[rt].l, l, tree[rt].l);
        }
        pushup(rt);
    }
    inline void insert(int x)
    {
        int rt1, rt2;
        split_val(root, rt1, rt2, x - 1);
        merge(rt1, rt1, newnode(x));
        merge(root, rt1, rt2);
        return;
    }
    inline void del(int val)
    {
        int x, y, z;
        split_val(root, x, y, val);
        split_val(x, x, z, val - 1);
        merge(z, tree[z].l, tree[z].r);
        merge(x, x, z);
        merge(root, x, y);
    }
    inline int rnk(int val)
    {
        int x, y;
        split_val(root, x, y, val - 1);
        int ans = tree[x].sz + 1;
        merge(root, x, y);
        return ans;
    }
    inline int kth(int root, int k)
    {
        int x = root;
        while (true)
        {
            if (k == tree[tree[x].l].sz + 1)
                return tree[x].val;
            if (k <= tree[tree[x].l].sz)
                x = tree[x].l;
            else
                k -= tree[tree[x].l].sz + 1, x = tree[x].r;
        }
    }
    inline int kth(int k)
    {
        return kth(root, k);
    }
    inline int pre(int val)
    {
        int x, y;
        split_val(root, x, y, val - 1);
        int ans = kth(x, tree[x].sz);
        merge(root, x, y);
        return ans;
    }
    inline int suf(int val)
    {
        int x, y;
        split_val(root, x, y, val);
        int ans = kth(y, 1);
        merge(root, x, y);
        return ans;
    }
};
Treap tr;
signed main()
{
    int n;
    cin >> n;
    while (n--)
    {
        int op, x;
        cin >> op >> x;
        if (op == 1)
        {
            tr.insert(x);
        }
        else if (op == 2)
        {
            tr.del(x);
        }
        else if (op == 3)
        {
            cout << tr.rnk(x) << endl;
        }
        else if (op == 4)
        {
            cout << tr.kth(x) << endl;
        }
        else if (op == 5)
        {
            cout << tr.pre(x) << endl;
        }
        else
            cout << tr.suf(x) << endl;
    }
}

6.1.2.2.2 单个节点有多个值，相同值使用同一个个节点，不支持split_sz

random_device rd;
mt19937 ran(rd());
struct Treap
{
    struct node
    {
        int l, r;
        int val;
        int sz;
        int cnt;
        int w;
        node() : l(0), r(0), val(0), sz(0), cnt(0), w(0) {};
        node(int val) : l(0), r(0), val(val), sz(1), cnt(1), w(ran()) {};
    };
    const static int N = 2e6 + 9;
    int tot = 0;
    int root = 0;
    node tree[N];
    int newnode(int val)
    {
        tot++;
        tree[tot] = node(val);
        return tot;
    }
    void pushup(int rt)
    {
        tree[rt].sz = tree[tree[rt].l].sz + tree[tree[rt].r].sz + tree[rt].cnt;
        return;
    }
    void merge(int &rt, const int l, const int r)
    {
        if (!l || !r)
        {
            rt = l | r;
            return;
        }
        if (tree[l].w > tree[r].w)
        {
            rt = l;
            merge(tree[rt].r, tree[rt].r, r);
        }
        else
        {
            rt = r;
            merge(tree[rt].l, l, tree[rt].l);
        }
        pushup(rt);
        return;
    }
    void split_val(const int rt, int &l, int &r, int val)
    {
        if (!rt)
        {
            l = r = 0;
            return;
        }
        if (tree[rt].val <= val)
        {
            l = rt;
            split_val(tree[rt].r, tree[rt].r, r, val);
        }
        else
        {
            r = rt;
            split_val(tree[rt].l, l, tree[rt].l, val);
        }
        pushup(rt);
    }
    inline void insert(int x)
    {
        int rt1, rt2, rt3;
        split_val(root, rt1, rt2, x - 1);
        split_val(rt2, rt2, rt3, x);
        if (!rt2)
            rt2 = newnode(x);
        else
            tree[rt2].cnt++, tree[rt2].sz++;
        merge(rt2, rt2, rt3);
        merge(root, rt1, rt2);
        return;
    }
    inline void del(int val)
    {
        int rt1, rt2, rt3;
        split_val(root, rt1, rt2, val);
        split_val(rt1, rt1, rt3, val - 1);
        assert(rt3 != 0);
        tree[rt3].cnt--, tree[rt3].sz--;
        if (!tree[rt3].cnt)
            merge(rt3, tree[rt3].l, tree[rt3].r);
        merge(rt1, rt1, rt3);
        merge(root, rt1, rt2);
        return;
    }
    inline int rnk(int val)
    {
        int x, y;
        split_val(root, x, y, val - 1);
        int ans = tree[x].sz + 1;
        merge(root, x, y);
        return ans;
    }
    inline int kth(int root, int k)
    {
        int x = root;
        while (true)
        {
            if (k <= tree[tree[x].l].sz)
            {
                x = tree[x].l;
            }
            else if (k > tree[tree[x].l].sz + tree[x].cnt)
            {
                k -= (tree[tree[x].l].sz + tree[x].cnt);
                x = tree[x].r;
            }
            else
            {
                return tree[x].val;
            }
        }
    }
    inline int kth(int k)
    {
        return kth(root, k);
    }
    inline int pre(int val)
    {
        int x, y;
        split_val(root, x, y, val - 1);
        int ans = kth(x, tree[x].sz);
        merge(root, x, y);
        return ans;
    }
    inline int suf(int val)
    {
        int x, y;
        split_val(root, x, y, val);
        int ans = kth(y, 1);
        merge(root, x, y);
        return ans;
    }
};
Treap tr;

6.1.3 伸展树（Splay Tree）

通过 $Splay$ /伸展操作 不断将某个节点旋转到根节点，使得整棵树仍然满足二叉查找树的性质，能够在均摊 $O(logN)$ 时间内完成插入，查找和删除操作，并且保持平衡而不至于退化为链。

每次操作之后，被操作数均在根节点。

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 100005;
int rt, tot, fa[N], ch[N][2], val[N], cnt[N], sz[N];
struct Splay
{
    void maintain(int x) { sz[x] = sz[ch[x][0]] + sz[ch[x][1]] + cnt[x]; }

    bool get(int x) { return x == ch[fa[x]][1]; }

    void clear(int x)
    {
        ch[x][0] = ch[x][1] = fa[x] = val[x] = sz[x] = cnt[x] = 0;
    }

    void rotate(int x)
    {
        int y = fa[x], z = fa[y], chk = get(x);
        ch[y][chk] = ch[x][chk ^ 1];
        if (ch[x][chk ^ 1])
            fa[ch[x][chk ^ 1]] = y;
        ch[x][chk ^ 1] = y;
        fa[y] = x;
        fa[x] = z;
        if (z)
            ch[z][y == ch[z][1]] = x;
        maintain(y);
        maintain(x);
    }

    void splay(int x, int goal = 0)
    {
        if (goal == 0)
            rt = x;
        while (fa[x] != goal)
        {
            int f = fa[x], g = fa[fa[x]];
            if (g != goal)
            {
                if (get(f) == get(x))
                    rotate(f);
                else
                    rotate(x);
            }
            rotate(x);
        }
    }

    void ins(int k)
    {
        if (!rt)
        {
            val[++tot] = k;
            cnt[tot]++;
            rt = tot;
            maintain(rt);
            return;
        }
        int cur = rt, f = 0;
        while (1)
        {
            if (val[cur] == k)
            {
                cnt[cur]++;
                maintain(cur);
                maintain(f);
                splay(cur);
                break;
            }
            f = cur;
            cur = ch[cur][val[cur] < k];
            if (!cur)
            {
                val[++tot] = k;
                cnt[tot]++;
                fa[tot] = f;
                ch[f][val[f] < k] = tot;
                maintain(tot);
                maintain(f);
                splay(tot);
                break;
            }
        }
    }

    int rk(int k)
    {
        int res = 0, cur = rt;
        while (1)
        {
            if (k < val[cur])
            {
                cur = ch[cur][0];
            }
            else
            {
                res += sz[ch[cur][0]];
                if (!cur)
                    return res + 1;
                if (k == val[cur])
                {
                    splay(cur);
                    return res + 1;
                }
                res += cnt[cur];
                cur = ch[cur][1];
            }
        }
    }

    int kth(int k)
    {
        int cur = rt;
        while (1)
        {
            if (ch[cur][0] && k <= sz[ch[cur][0]])
            {
                cur = ch[cur][0];
            }
            else
            {
                k -= cnt[cur] + sz[ch[cur][0]];
                if (k <= 0)
                {
                    splay(cur);
                    return val[cur];
                }
                cur = ch[cur][1];
            }
        }
    }
    // 返回前驱结点根编号
    int pre()
    {
        int cur = ch[rt][0];
        if (!cur)
            return cur;
        while (ch[cur][1])
            cur = ch[cur][1];
        splay(cur);
        return cur;
    }
    // 返回后继结点根编号
    int nxt()
    {
        int cur = ch[rt][1];
        if (!cur)
            return cur;
        while (ch[cur][0])
            cur = ch[cur][0];
        splay(cur);
        return cur;
    }

    void del(int k)
    {
        rk(k);
        if (cnt[rt] > 1)
        {
            cnt[rt]--;
            maintain(rt);
            return;
        }
        if (!ch[rt][0] && !ch[rt][1])
        {
            clear(rt);
            rt = 0;
            return;
        }
        if (!ch[rt][0])
        {
            int cur = rt;
            rt = ch[rt][1];
            fa[rt] = 0;
            clear(cur);
            return;
        }
        if (!ch[rt][1])
        {
            int cur = rt;
            rt = ch[rt][0];
            fa[rt] = 0;
            clear(cur);
            return;
        }
        int cur = rt;
        int x = pre();
        fa[ch[cur][1]] = x;
        ch[x][1] = ch[cur][1];
        clear(cur);
        maintain(rt);
    }
} tree;

int main()
{
    int n, opt, x;
    for (scanf("%d", &n); n; --n)
    {
        scanf("%d%d", &opt, &x);
        if (opt == 1)
            tree.ins(x);
        else if (opt == 2)
            tree.del(x);
        else if (opt == 3)
            printf("%d\n", tree.rk(x));
        else if (opt == 4)
            printf("%d\n", tree.kth(x));
        else if (opt == 5)
            tree.ins(x), printf("%d\n", val[tree.pre()]), tree.del(x);
        else
            tree.ins(x), printf("%d\n", val[tree.nxt()]), tree.del(x);
    }
    return 0;
}

6.2 文艺平衡树

文艺平衡树，指借助平衡树中序遍历是从小到大的性质将其略作修改，用于维护高级区间操作行为（例如，维护区间 $[l,r]$ 翻转），不支持一切传统平衡树操作。

请写一个程序，要求维护一个数列，支持以下 $6$ 种操作：

编号	名称	格式	说明
1	插入	$\operatorname{INSERT}\ posi \ tot \ c_1 \ c_2 \cdots c_{tot}$	在当前数列的第 $posi$ 个数字后插入 $tot$ 个数字： $c_1, c_2 \cdots c_{tot}$ ；若在数列首插入，则 $posi$ 为 $0$
2	删除	$\operatorname{DELETE} \ posi \ tot$	从当前数列的第 $posi$ 个数字开始连续删除 $tot$ 个数字
3	修改	$\operatorname{MAKE-SAME} \ posi \ tot \ c$	从当前数列的第 $posi$ 个数字开始的连续 $tot$ 个数字统一修改为 $c$
4	翻转	$\operatorname{REVERSE} \ posi \ tot$	取出从当前数列的第 $posi$ 个数字开始的 $tot$ 个数字，翻转后放入原来的位置
5	求和	$\operatorname{GET-SUM} \ posi \ tot$	计算从当前数列的第 $posi$ 个数字开始的 $tot$ 个数字的和并输出
6	求最大子列和	$\operatorname{MAX-SUM}$	求出当前数列中和最大的一段子列，并输出最大和

对于 $100\%$ 的数据，任何时刻数列中最多含有 $5 \times 10^5$ 个数，任何时刻数列中任何一个数字均在 $[-10^3, 10^3]$ 内， $1 \le M \le 2 \times 10^4$ ，插入的数字总数不超过 $4 \times 10^6$ 。

6.2.1 无旋Treap实现文艺平衡树

懒标记和线段树的想法一样，这样处理不容易错。

分裂要按size，交换是整个子树内的所有节点的 $lson,rson$ 全部交换，所以需要懒标记。交换儿子并不会影响堆的性质，所以不需要管。

更复杂的懒标记一定要搞清楚。搞不清楚懒标记极其容易错且相当难以调试（因为树结构的随机性）

这个题标记的坑点就在于子段长度非空，全负数就要输出最大的那个负数。所以维护区间中值（区间最大子段）的时候需要额外带一次tree[rt].val，详情见懒标记。

#include <bits/stdc++.h>
using namespace std;
random_device rd;
mt19937 ran(rd());
#define int long long
struct Treap
{
    struct node
    {
        int l, r;
        int w;
        int val;
        int sz;
        int lazytag;
        int sum;
        int maxsum;
        int maxpresum;
        int maxsufsum;
        bool sametag;
        int sames;
        node() : l(0), r(0), w(0), val(0),
                 sz(0), lazytag(0), sum(0), maxpresum(0), maxsufsum(0),
                 sametag(0), sames(0), maxsum(0) {};
        node(int val) : l(0), r(0), w(ran()), val(val),
                        sz(1), lazytag(0), sum(val), maxpresum(max(val, 0ll)),
                        maxsufsum(max(val, 0ll)), sametag(0), sames(0), maxsum(val) {};
    };
    const static int maxn = 5e5 + 9;
    node tree[maxn];
    int root;
    queue<int> q;
    inline void init()
    {
        for (int i = 1; i < maxn; i++)
        {
            q.push(i);
        }
    }
    Treap() { init(); }
    int newnode(int val)
    {
        int tot = q.front();
        q.pop();
        tree[tot] = node(val);
        return tot;
    }
    void getrub(int rt)
    {
        if (!rt)
            return;
        getrub(tree[rt].l);
        getrub(tree[rt].r);
        q.push(rt);
        tree[rt] = node();
        return;
    }
    void pushup(int rt)
    {
        tree[rt].sz = tree[tree[rt].l].sz + tree[tree[rt].r].sz + 1;

        tree[rt].sum = tree[tree[rt].l].sum + tree[tree[rt].r].sum + tree[rt].val;

        tree[rt].maxpresum = max(tree[tree[rt].l].maxpresum, tree[tree[rt].l].sum + tree[rt].val + tree[tree[rt].r].maxpresum);

        tree[rt].maxsufsum = max(tree[tree[rt].r].maxsufsum, tree[tree[rt].r].sum + tree[rt].val + tree[tree[rt].l].maxsufsum);

        tree[rt].maxsum = max(tree[rt].val, tree[tree[rt].l].maxsufsum + tree[rt].val + tree[tree[rt].r].maxpresum);

        if (tree[rt].l)
        {
            tree[rt].maxsum = max(tree[rt].maxsum, tree[tree[rt].l].maxsum);
        }
        if (tree[rt].r)
        {
            tree[rt].maxsum = max(tree[rt].maxsum, tree[tree[rt].r].maxsum);
        }

        return;
    }
    void Reverse(int x)
    {
        if (!x)
            return;
        swap(tree[x].l, tree[x].r);
        swap(tree[x].maxpresum, tree[x].maxsufsum);
        tree[x].lazytag ^= 1;
    }
    void Cover(int rt, int ci)
    {
        tree[rt].val = tree[rt].sames = ci;
        tree[rt].sum = tree[rt].sz * ci;
        tree[rt].maxpresum = tree[rt].maxsufsum = max(0ll, tree[rt].sum);
        tree[rt].maxsum = max(ci, tree[rt].sum);
        tree[rt].sametag = 1;
    }
    void pushdown(int rt)
    {
        if (!rt)
            return;
        if (tree[rt].lazytag)
        {
            if (tree[rt].l)
                Reverse(tree[rt].l);
            if (tree[rt].r)
                Reverse(tree[rt].r);
            tree[rt].lazytag = 0;
        }
        if (tree[rt].sametag)
        {
            if (tree[rt].l)
            {
                Cover(tree[rt].l, tree[rt].sames);
            }
            if (tree[rt].r)
            {
                Cover(tree[rt].r, tree[rt].sames);
            }
            tree[rt].sametag = 0;
            tree[rt].sames = 0;
        }
    }
    void split_sz(const int rt, int &l, int &r, int sz)
    {
        if (!rt)
        {
            l = r = 0;
            return;
        }
        pushdown(rt);
        if (tree[tree[rt].l].sz + 1 <= sz)
        {
            l = rt;
            split_sz(tree[rt].r, tree[rt].r, r, sz - (tree[tree[rt].l].sz + 1));
        }
        else
        {
            r = rt;
            split_sz(tree[rt].l, l, tree[rt].l, sz);
        }
        pushup(rt);
    }
    void merge(int &rt, const int l, const int r)
    {
        if (!l || !r)
        {
            rt = l | r;
            return;
        }
        pushdown(l);
        pushdown(r);
        if (tree[l].w > tree[r].w) // 大根堆形式，小根堆换个号就行
        {
            rt = l;
            merge(tree[rt].r, tree[rt].r, r);
        }
        else
        {
            rt = r;
            merge(tree[rt].l, l, tree[rt].l);
        }
        pushup(rt);
    }
    void insert(int pos, vector<int> &a)
    {
        int rt1, rt2;
        split_sz(root, rt1, rt2, pos);
        for (auto j : a)
        {
            merge(rt1, rt1, newnode(j));
        }
        merge(root, rt1, rt2);
    }
    void del(int pos, int tot)
    {
        int rt1, rt2, rt3;
        split_sz(root, rt1, rt3, pos + tot - 1);
        split_sz(rt1, rt1, rt2, pos - 1);
        getrub(rt2);
        merge(root, rt1, rt3);
    }
    void reverse(int l, int tot)
    {
        int rt1, rt2, rt3;
        split_sz(root, rt2, rt3, l + tot - 1);
        split_sz(rt2, rt1, rt2, l - 1);
        Reverse(rt2);
        merge(rt2, rt1, rt2);
        merge(root, rt2, rt3);
    }
    int getsum(int pos, int tot)
    {
        int rt1, rt2, rt3;
        split_sz(root, rt1, rt3, pos + tot - 1);
        split_sz(rt1, rt1, rt2, pos - 1);
        int ans = tree[rt2].sum;
        merge(rt1, rt1, rt2);
        merge(root, rt1, rt3);
        return ans;
    }
    int getmaxsum()
    {
        return tree[root].maxsum;
    }
    void make_same(int l, int tot, int c)
    {
        int rt1, rt2, rt3;
        split_sz(root, rt2, rt3, l + tot - 1);
        split_sz(rt2, rt1, rt2, l - 1);
        Cover(rt2, c);
        merge(rt2, rt1, rt2);
        merge(root, rt2, rt3);
    }
    void print(int rt)
    {
        if (!rt)
            return;
        pushdown(rt);
        print(tree[rt].l);
        cout << tree[rt].val << " ";
        print(tree[rt].r);
    }
    void print()
    {
        print(root);
        cout << endl;
        return;
    }
};
Treap tr;
signed main()
{
    // freopen("data.in", "r", stdin);
    // freopen("data.out", "w", stdout);
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int n, m;
    cin >> n >> m;
    vector<int> a(n);
    for (auto &i : a)
        cin >> i;
    tr.insert(0, a);
    while (m--)
    {
        string s;
        cin >> s;
        if (s == "GET-SUM")
        {
            int pos, cnt;
            cin >> pos >> cnt;
            cout << tr.getsum(pos, cnt) << endl;
        }
        else if (s == "MAX-SUM")
        {
            cout << tr.getmaxsum() << endl;
        }
        else if (s == "INSERT")
        {
            int pos, cnt;
            cin >> pos >> cnt;
            vector<int> b(cnt);
            for (auto &j : b)
                cin >> j;
            tr.insert(pos, b);
        }
        else if (s == "DELETE")
        {
            int pos, cnt;
            cin >> pos >> cnt;
            tr.del(pos, cnt);
        }
        else if (s == "MAKE-SAME")
        {
            int pos, tot, c;
            cin >> pos >> tot >> c;
            tr.make_same(pos, tot, c);
        }
        else
        {
            int pos, tot;
            cin >> pos >> tot;
            tr.reverse(pos, tot);
        }
        // tr.print();
    }
}

6.3 可持久化平衡树

如题，可持久化数据结构。

需要注意一点，平衡树可持久化消耗无用内存更大，建议空间倍数<<6以上

6.3.1 可持久化无旋Treap

和非可持久化无旋 $Treap$ 几乎没有区别，小简单的差异出在merge和split_val函数上，每次要分裂或者要合并的时候都必须新开结点，将复制一份旧结点，以保证原先版本不被破坏。

用于解决需要提供以下操作的数据结构（ 对于各个以往的历史版本 ）：

1、插入 $x$

2、删除 $x$ （若有多个相同的数，应只删除一个，如果没有请忽略该操作）

3、查询 $x$ 的排名（排名定义为比当前数小的数的个数 $+1$ ）

4、查询排名为 $x$ 的数

5、求 $x$ 的前驱（前驱定义为小于 $x$ ，且最大的数，如不存在输出 $-2^{31}+1$ ）

6、求 $x$ 的后继（后继定义为大于 $x$ ，且最小的数，如不存在输出 $2^{31}-1$ ）

和原本平衡树不同的一点是，每一次的任何操作都是基于某一个历史版本，同时生成一个新的版本。（操作3, 4, 5, 6即保持原版本无变化）

每个版本的编号即为操作的序号（版本 $0$ 即为初始状态，空树）
对于 $100\%$ 的数据， $ 1 \leq n \leq 5 \times 10^5 $ , $|x_i| \leq {10}^9$ ， $0 \le v_i < i$ ， $1\le \text{opt} \le 6$ 。

#include <bits/stdc++.h>
using namespace std;
random_device rd;
mt19937 ran(rd());
struct Persistant_Treap
{
    struct node
    {
        int l, r;
        int val;
        int sz;
        int cnt;
        int w;
        node() { l = r = val = sz = cnt = w = 0; };
        node(int val) : l(0), r(0), val(val), sz(1), cnt(1), w(ran()) {}
    };
    int tot = 0;
    const static int maxn = 5e5 + 9;
    node tree[maxn << 6];
    int vers[maxn];
    int ver = 0;
    int newnode(int val)
    {
        ++tot;
        tree[tot] = node(val);
        return tot;
    }
    void pushup(int rt)
    {
        tree[rt].sz = tree[rt].cnt + tree[tree[rt].l].sz + tree[tree[rt].r].sz;
        return;
    }
    int merge(const int l, const int r)
    {
        if (!l || !r)
            return l | r;
        int newrt;
        if (tree[l].w > tree[r].w)
        {
            newrt = ++tot;
            tree[newrt] = tree[l];
            tree[newrt].r = merge(tree[newrt].r, r);
        }
        else
        {
            newrt = ++tot;
            tree[newrt] = tree[r];
            tree[newrt].l = merge(l, tree[newrt].l);
        }
        pushup(newrt);
        return newrt;
    }
    void split_val(int rt, int &l, int &r, int val)
    {
        if (!rt)
        {
            l = r = 0;
            return;
        }
        int newrt;
        if (tree[rt].val <= val)
        {
            l = ++tot;
            tree[l] = tree[rt];
            split_val(tree[rt].r, tree[l].r, r, val);
            pushup(l);
        }
        else
        {
            r = ++tot;
            tree[r] = tree[rt];
            split_val(tree[rt].l, l, tree[r].l, val);
            pushup(r);
        }
    }
    inline void insert(int v, int val)
    {
        vers[++ver] = vers[v];
        int rt1, rt2, rt3;
        split_val(vers[ver], rt1, rt2, val - 1);
        split_val(rt2, rt2, rt3, val);
        if (!rt2)
            rt2 = newnode(val);
        else
            tree[rt2].cnt++, tree[rt2].sz++;
        rt2 = merge(rt2, rt3);
        vers[ver] = merge(rt1, rt2);
        return;
    }
    inline void del(int v, int val)
    {
        vers[++ver] = vers[v];
        int rt1, rt2, rt3;
        split_val(vers[ver], rt1, rt2, val);
        split_val(rt1, rt1, rt3, val - 1);
        if (!rt3)
            return;
        tree[rt3].cnt--, tree[rt3].sz--;
        if (!tree[rt3].cnt)
            rt3 = merge(tree[rt3].l, tree[rt3].r);
        rt1 = merge(rt1, rt3);
        vers[ver] = merge(rt1, rt2);
        return;
    }
    inline int rnk(int v, int val)
    {
        vers[++ver] = vers[v];
        int x, y;
        split_val(vers[ver], x, y, val - 1);
        int ans = tree[x].sz + 1;
        vers[ver] = merge(x, y);
        return ans;
    }
    inline int kth(int v, int k) // 版本访问
    {
        vers[++ver] = vers[v];
        int x = vers[ver];
        while (true)
        {
            if (k <= tree[tree[x].l].sz)
            {
                x = tree[x].l;
            }
            else if (k > tree[tree[x].l].sz + tree[x].cnt)
            {
                k -= (tree[tree[x].l].sz + tree[x].cnt);
                x = tree[x].r;
            }
            else
            {
                return tree[x].val;
            }
        }
    }
    inline int _kth(int rt, int k) // 根访问，private
    {
        int x = rt;
        while (true)
        {
            if (k <= tree[tree[x].l].sz)
            {
                x = tree[x].l;
            }
            else if (k > tree[tree[x].l].sz + tree[x].cnt)
            {
                k -= (tree[tree[x].l].sz + tree[x].cnt);
                x = tree[x].r;
            }
            else
            {
                return tree[x].val;
            }
        }
    }
    inline int pre(int v, int val)
    {
        vers[++ver] = vers[v];
        int x, y;
        split_val(vers[ver], x, y, val - 1);

        int ans = -(INT_MAX);
        if (x != 0)
            ans = _kth(x, tree[x].sz);
        vers[ver] = merge(x, y);
        return ans;
    }
    inline int suf(int v, int val)
    {
        vers[++ver] = vers[v];
        int x, y;
        split_val(vers[ver], x, y, val);
        int ans = (INT_MAX);
        if (y != 0)
            ans = _kth(y, 1);
        vers[ver] = merge(x, y);
        return ans;
    }
};
Persistant_Treap tr;
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin >> n;
    while (n--)
    {
        int v, op, x;
        cin >> v >> op >> x;
        if (op == 1)
        {
            tr.insert(v, x);
        }
        else if (op == 2)
        {
            tr.del(v, x);
        }
        else if (op == 3)
        {
            cout << tr.rnk(v, x) << endl;
        }
        else if (op == 4)
        {
            cout << tr.kth(v, x) << endl;
        }
        else if (op == 5)
        {
            cout << tr.pre(v, x) << endl;
        }
        else
            cout << tr.suf(v, x) << endl;
    }
}

6.3.2 可持久化文艺平衡树

理论上，文艺平衡树可以干了线段树所能干的所有活儿，但是常数 $SuperBig$ 。其存活意义主要在于区间翻转。

维护一个序列，其中需要提供以下操作，要求强制在线（对于各个以往的历史版本）：

在第 $p$ 个数后插入数 $x$ 。
删除第 $p$ 个数。
翻转区间 $[l,r]$ ，例如原序列是 $\{5,4,3,2,1\}$ ，翻转区间 $[2,4]$ 后，结果是 $\{5,2,3,4,1\}$ 。
查询区间 $[l,r]$ 中所有数的和。

和原本平衡树不同的一点是，每一次的任何操作都是基于某一个历史版本，同时生成一个新的版本（操作 $4$ 即保持原版本无变化），新版本即编号为此次操作的序号。

emm,相当贴内存 $(979MB/1GB)$ ，爆 $\color{red}MLE$ 就看着办吧。

注意，pushdown的时候也要新建立拷贝节点，记住，可持久化数据结构上只要涉及到改必须要新建节点。

#include <bits/stdc++.h>
using namespace std;
random_device rd;
mt19937 ran(rd());
#define i64 long long
struct Persistant_literary_Treap
{
private:
    struct node
    {
        int l, r;
        int w;
        i64 sum;
        i64 val;
        bool lazy;
        int sz;
        node() { l = r = w = sum = val = sz = lazy = 0; };
        node(i64 val) : l(0), r(0), w(ran()), sum(val), val(val), sz(1), lazy(0) {}
    };
    const static int maxn = 2e5 + 9;
    node tree[maxn << 7];
    int vers[maxn], ver = 0;
    int tot = 0;
    int newnode(i64 val)
    {
        tot++;
        tree[tot] = node(val);
        return tot;
    }
    void pushdown(int rt)
    {
        if (!rt)
            return;
        if (!tree[rt].lazy)
            return;
        if (tree[rt].l) // 只要动结点那必须全部备份可持久化
        {
            int rl = ++tot;
            tree[rl] = tree[tree[rt].l];
            tree[rt].l = rl;
        }
        if (tree[rt].r)
        {
            int rr = ++tot;
            tree[rr] = tree[tree[rt].r];
            tree[rt].r = rr;
        }
        swap(tree[rt].l, tree[rt].r);
        if (tree[rt].l)
            tree[tree[rt].l].lazy ^= 1;
        if (tree[rt].r)
            tree[tree[rt].r].lazy ^= 1;
        tree[rt].lazy = 0;
        return;
    }
    void pushup(int rt)
    {
        tree[rt].sz = tree[tree[rt].l].sz + tree[tree[rt].r].sz + 1;
        tree[rt].sum = tree[tree[rt].l].sum + tree[tree[rt].r].sum + tree[rt].val;
        return;
    }
    int merge(int l, int r)
    {
        if (!l || !r)
            return l | r;
        int nowrt = 0;
        pushdown(l);
        pushdown(r);
        if (tree[l].w > tree[r].w)
        {
            nowrt = ++tot;
            tree[nowrt] = tree[l];
            tree[nowrt].r = merge(tree[nowrt].r, r);
            pushup(nowrt);
        }
        else
        {
            nowrt = ++tot;
            tree[nowrt] = tree[r];
            tree[nowrt].l = merge(l, tree[nowrt].l);
            pushup(nowrt);
        }
        return nowrt;
    }
    void split_sz(const int rt, int &l, int &r, int sz)
    {
        if (!rt)
        {
            l = r = 0;
            return;
        }
        pushdown(rt);
        if (tree[tree[rt].l].sz + 1 <= sz)
        {
            int newrt = ++tot;
            tree[newrt] = tree[rt];
            l = newrt;
            split_sz(tree[rt].r, tree[newrt].r, r, sz - (tree[tree[newrt].l].sz + 1));
            pushup(l);
        }
        else
        {
            int newrt = ++tot;
            tree[newrt] = tree[rt];
            r = newrt;
            split_sz(tree[rt].l, l, tree[newrt].l, sz);
            pushup(r);
        }
        return;
    }

public:
    inline void insert(int v, int k, i64 val)
    {
        vers[++ver] = vers[v];
        int rt1, rt2;
        split_sz(vers[ver], rt1, rt2, k);
        rt1 = merge(rt1, newnode(val));
        vers[ver] = merge(rt1, rt2);
        return;
    }
    inline void del(int v, int k)
    {
        vers[++ver] = vers[v];
        int rt1, rt2, rt3;
        split_sz(vers[ver], rt1, rt3, k);
        split_sz(rt1, rt1, rt2, k - 1);
        vers[ver] = merge(rt1, rt3);
        return;
    }
    inline i64 query(int v, int l, int r)
    {
        vers[++ver] = vers[v];
        int rt1, rt2, rt3;
        split_sz(vers[ver], rt1, rt3, r);
        split_sz(rt1, rt1, rt2, l - 1);
        i64 ans = tree[rt2].sum;
        rt1 = merge(rt1, rt2);
        vers[ver] = merge(rt1, rt3);
        return ans;
    }
    inline void reverse(int v, int l, int r)
    {
        vers[++ver] = vers[v];
        int rt1, rt2, rt3;
        split_sz(vers[ver], rt1, rt3, r);
        split_sz(rt1, rt1, rt2, l - 1);
        tree[rt2].lazy ^= 1;
        rt1 = merge(rt1, rt2);
        vers[ver] = merge(rt1, rt3);
        return;
    }
};
Persistant_literary_Treap tr;
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int n;
    cin >> n;
    i64 lastans = 0;
    while (n--)
    {
        i64 v, op, p, x, l, r;
        cin >> v >> op;
        if (op == 1)
        {
            cin >> p >> x;
            p ^= lastans;
            x ^= lastans;
            tr.insert(v, p, x);
        }
        else if (op == 2)
        {
            cin >> p;
            p ^= lastans;
            tr.del(v, p);
        }
        else if (op == 3)
        {
            cin >> l >> r;
            l ^= lastans;
            r ^= lastans;
            tr.reverse(v, l, r);
        }
        else
        {
            cin >> l >> r;
            l ^= lastans;
            r ^= lastans;
            lastans = tr.query(v, l, r);
            cout << lastans << endl;
        }
    }
}

7.树套树

7.1 线段树套平衡树

关键词：区间大型平衡树操作。

您需要写一种数据结构（可参考题目标题），来维护一个有序数列，其中需要提供以下操作：

查询 $k$ 在区间内的排名
查询区间内排名为 $k$ 的值
修改某一位置上的数值
查询 $k$ 在区间内的前驱（前驱定义为严格小于 $x$ ，且最大的数，若不存在输出 -2147483647）
查询 $k$ 在区间内的后继（后继定义为严格大于 $x$ ，且最小的数，若不存在输出 2147483647）

$1\le n,m\le5\times 10^4$ ，序列中的值在任何时刻 $\in[0,10^8]$ 。

（特别提醒：此数据不保证操作 4、5 一定存在，故请务必考虑不存在的情况。）

做法：

每个线段树结点维护一个 $Treap$ 平衡树，区间合并直接平衡树 $Merge$ 拿下。

查询排名：线段树查询，查询每个子区间内 $(k-1)$ 的排名并求和，复杂度 $O(logN)$
查询排名为 $k$ 的数：这个没办法直接加法求，需要二分+操作1判断，复杂度 $O(log^2N)$
修改：无话可说，复杂度 $O(logN)$ 。
查询前驱：各区间查询前驱后取 $max$ ，复杂度 $O(logN)$ 。
查询后继：各区间查询后继后取 $min$ ，复杂度 $O(logN)$ .

复杂度上界 $O(Nlog^3N)$ 。单纯修改+查询第 $K$ 小树状主席树可以 $O(Nlog^2N)$ 实现。

7.2 树状数组+线段树

关键词：主席树强化，差分动态开点线段树

树状数组的差分性质使得主席树可以支持快速修改。

见1.12

*7.3 线段树套线段树

关键词：二维区间修改、区间查询。

见 $OI-Wiki$ 手册，过于偏门。

8. 静态树（树上差分；HLD/LLD，重链剖分、长链剖分）

关键词：静态树区间操作，静态树序列化操作。

8.1 树上差分——静态树，静态树节点信息

想操作、查询 $u$ 到 $v$ 节点的区间属性，可以通过树上差分到根操作实现，即结点 $u$ 存储 $u$ 到根的信息， $v$ 存储 $v$ 到根的信息。

查询的时候直接查询 $u+v-lca_{u,v}-fa_{lca_{u,v}}$ 即可。

#include <bits/stdc++.h>//树上差分，树上一条链的区间和，from：[JLOI2014] 松鼠的新家
using namespace std;
const int inf=0x3f3f3f3f;
const int N=3*1e5+10;
int n,u,v,vis[N],a[N],b[N];
int fa[N][40],dep[N];
vector<int>edge[N];
void dfs(int x,int f){//lca预处理
    dep[x]=dep[f]+1;
    fa[x][0]=f;
    for(auto i:edge[x])if(i!=f)dfs(i,x); 
}
void sum(int x,int f){//统计点x的值
    a[x]=b[x];
    for(auto i:edge[x]){
        if(i!=f){
            sum(i,x);//此时已经统计了所有i的值了
            a[x]+=a[i];
        }
    }
}
int lca(int x,int y){//lca
    if(x==y)return x;
    if(dep[x]<dep[y])swap(x,y);
    for(int i=30;i>=0;i--)
        if(dep[fa[x][i]]>=dep[y])x=fa[x][i];
    if(x==y)return x;
    for(int i=30;i>=0;i--)
        if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];
    return fa[x][0];
}
int main(){
    cin>>n;
    for(int i=1;i<=n;i++)cin>>vis[i];
    for(int i=1;i<=n-1;i++){
        cin>>u>>v;
        edge[u].push_back(v);
        edge[v].push_back(u);
    }
    dfs(1,0);
    for(int j=1;j<=30;j++)
        for(int i=1;i<=n;i++)
            fa[i][j]=fa[fa[i][j-1]][j-1];
    for(int i=1;i<=n-1;i++){//点差分,一个点的差分数组的值就是这个点的值-所有其亲儿子的值
    //对vis[i],vis[i+1]这两个点之间加一只需要如下步骤（四步），操作的是差分数组
        b[vis[i]]++;
        b[vis[i+1]]++;
        b[lca(vis[i],vis[i+1])]--;
        b[fa[lca(vis[i],vis[i+1])][0]]--;
    }
    sum(1,0);//遍历整棵树，推出原始权值
    for(int i=2;i<=n;i++)a[vis[i]]--;//本题例外（因为我们把既作为起点又做为终点的点算了两次，现在把这些点的权值减一即可 ）
    for(int i=1;i<=n;i++)cout<<a[i]<<endl;
    return 0;
}

还有一个树上异或差分：

#include<bits/stdc++.h>
#define int long long
#define lowbit(x) (x&-x)
#define endl '\n'//交互题就删
using namespace std;
const int N=1e6+10;
int n,q,u,v,idx,s,w;
int tree[N],a[N],dfn[N],dep[N],fa[N][21],siz[N];
vector<int>edge[N];
/*要求解决这样一个问题，满足以下两个操作：
1.u到v的路径上所有值异或上k
2.输出u到v上所有点的值
解法：
树上异或差分，1由异或的性质可以转化为四条链的操作，u->1，v->1，k->1，（k-fa）->1，但是可以简化，利用异或差分数组，一个点的值为这个点异或它的所有儿子节点，这样只需要修改u，v，k，k-fa四个点的值即可
2单点查询，难度在于如何通过异或差分还原这个点的值，方法就是u异或以u为根的子树的所有点的异或差分数组，利用dfs序，子树内的所有点被维护成了一个区间，这样就变成了区间异或，就可以利用树状数组快速维护，对dfs序建立树状数组即可。
//涉及知识点：异或、树状数组、dfs序、树上差分、异或前缀和、lca*/
void dfs(int x,int f){
    dep[x]=dep[f]+1;fa[x][0]=f;a[f]^=a[x],dfn[x]=++idx;
    siz[x]=1;
    for(auto i:edge[x]){
        if(i!=f){
            dfs(i,x);
            siz[x]+=siz[i];
        }
    }
}
void add(int x,int k){//点x加上k
    while(x<=n){
        tree[x]^=k;//依次修改每个覆盖有x的区间的值
        x+=lowbit(x);
    }
}
int sum(int x){//处理0到x之间的前缀和
    int cnt=0;
    while(x>0){
        cnt^=tree[x];
        x-=lowbit(x);
    }
    return cnt;
}
int lca(int x,int y){
    if(dep[x]>dep[y]) swap(x,y);//y的深度大，dep大
    for (int i=20;i>=0;i-- ) 
        if(dep[x]<=dep[y]-(1<<i)) y=fa[y][i];
    if(x==y) return x;
    for (int i=20;i>=0;i-- ) 
        if(fa[x][i]!=fa[y][i]) 
            x=fa[x][i],y=fa[y][i];
    return fa[x][0];
}
void change(int u,int v,int w){
    int k=lca(u,v);
    add(dfn[u],w);
    add(dfn[v],w);
    add(dfn[k],w);
    if (fa[k][0]) add(dfn[fa[k][0]], w);
}
int get(int u){
    return sum(dfn[u]+siz[u]-1)^sum(dfn[u]-1);
}
int check2(int u,int v){
    vector<int>e;int flag=0;
    if(dep[u]<dep[v])swap(u,v);
    while(dep[u]>dep[v]){
        e.push_back(get(u));
        u=fa[u][0];
    }
    if(u==v)e.push_back(get(u));
    else {
        while(u!=v){
            e.push_back(get(u));e.push_back(get(v));
            u=fa[u][0];v=fa[v][0];
        }
        e.push_back(get(u));
    }
    sort(e.begin(),e.end());
    for(int i=2;i<e.size();i++){
        if(e[i-2]+e[i-1]>e[i])return 1;
    }
    return 0;
}
int find(int u,int v){
    int k = lca(u, v);
    if (dep[u] + dep[v] - 2 * dep[k] + 1 > 46) return 1;
    else return check2(u,v);
}
signed main(){
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    cin>>n>>q;
    for(int i=1;i<=n;i++)cin>>a[i];
    for(int i=1;i<=n-1;i++){
        cin>>u>>v;
        edge[u].push_back(v);
        edge[v].push_back(u);
    }
    dfs(1,0);
    for(int j=1;j<=20;j++)
        for(int i=1;i<=n;i++)
            fa[i][j]=fa[fa[i][j-1]][j-1];
    for(int i=1;i<=n;i++)add(dfn[i],a[i]);
    for(int i=1;i<=q;i++){
        cin>>s;
        if(s==1){
            cin>>u>>v>>w;
            change(u,v,w);
        }
        else {
            cin>>u>>v;
            cout<<find(u,v);
        }
    }
}

8.2 重链剖分——静态树，动态树节点信息

一种以链节点数划分轻重以实现树节点编号化，将书上问题转移到区间操作实现。

重链剖分保证每一颗子树中所有节点的编号必定是一段连续的序列 $dfn$ 序号。

重链剖分可以将树上的任意一条路径划分成不超过 $logN$ 条连续的链，每条链上的点深度互不相同（即是自底向上的一条链，链上所有点的 $LCA$ 为链的一个端点)。

重链剖分还能保证划分出的每条链上的节点 DFS 序连续，因此可以方便地用一些维护序列的数据结构（如线段树）来维护树上路径的信息。

重链剖分复杂度是 $O(n)$ 的，两次 $dfs$ 实现，跳链求 $lca$ 的实现是单次询问 $O(logN)$ 的。对于高节点数而低强度询问相当友好。

这里默认是从 $1$ 开始的

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 3e5 + 9;
int father[maxn], sizes[maxn], hson[maxn], depth[maxn], top[maxn], ranks[maxn], dfn[maxn], cnt;
int nxt[maxn << 1LL], head[maxn], to[maxn << 1LL], tot;
void add(int u, int v)
{
    nxt[++tot] = head[u];
    head[u] = tot;
    to[tot] = v;
}
void add_edge(int u, int v)
{
    add(u, v);
    add(v, u);
}
void dfs1(int pos)
{
    hson[pos] = -1;
    sizes[pos] = 1;
    for (int i = head[pos]; i; i = nxt[i])
    {
        if (!depth[to[i]])
        {
            depth[to[i]] = depth[pos] + 1;
            father[to[i]] = pos;
            dfs1(to[i]);
            sizes[pos] += sizes[to[i]];
            if (hson[pos] == -1 || sizes[to[i]] > sizes[hson[pos]])
                hson[pos] = to[i];
        }
    }
}
void dfs2(int u, int tops)
{
    top[u] = tops;
    dfn[u] = ++cnt;
    ranks[cnt] = u;
    if (hson[u] != -1)
    {
        dfs2(hson[u], tops);
        for (int i = head[u]; i; i = nxt[i])
        {
            if (to[i] == father[u] || to[i] == hson[u])
                continue;
            dfs2(to[i], to[i]);
        }
    }
}
int n, m, r;
int a[maxn];
int lca(int u, int v)
{
    while (top[u] != top[v])
    {
        if (depth[top[u]] < depth[top[v]])
            swap(u, v);
        u = father[top[u]]; // 所在重链首低的向上跳
    }
    return depth[u] < depth[v] ? u : v;
}
void init()
{
    for (int i = 1; i < n; i++)
    {
        int u, v;
        cin >> u >> v;
        add_edge(u, v);
    }
    depth[r] = 1;
    dfs1(r);
    dfs2(r, r);
    // cout << "finished build" << endl;
    // cout << "root  is" << dfn[1] << endl;
    /*for (int i = 1; i <= n; i++)
        cout << dfn[i] << " ";
    cout << endl;
    for (int i = 1; i <= n; i++)
        cout << ranks[i] << " ";
    cout << endl;
    for (int i = 1; i <= n; i++)
        cout << top[i] << " ";
        */
    return;
}

8.3长链剖分——仅深度维度线性优化动态规划

长链剖分的实现方式和重链剖分很像，只不过重儿子被定义为了链长度最长的那一个，sz维护的是所属最长链的长度。

长链剖分跳链的时空复杂度最大是 $O(N\sqrt N)$ 的，这个道理显而易见。

长链剖分可以做到线性时间的优化树上和深度有关的 $dp$ 。长链剖分后，在维护信息的过程中，先 $O(1)$ 继承重儿子的信息，再暴力合并其余轻儿子的信息。

示例：

给定一棵以 $1$ 为根， $n$ 个节点的树。设 $d(u,x)$ 为 $u$ 子树中到 $u$ 距离为 $x$ 的节点数。

对于每个点，求一个最小的 $k$ ，使得 $d(u,k)$ 最大。 $1≤n≤10^6$

正常分析的话，设 $f_{u,i}$ 表示在 $u$ 子树中距离 $u$ 距离为 $i$ 的节点数，那么这个方程有：

$f_{u,i}=\sum f_{v,i-1}$

纯暴力转移，深度维度是 $O(n)$ ，总复杂度 $O(n^2)$ ，无法承受。

考虑树链剖分优化，对于 $u$ ，直接继承其重儿子的 $dp$ 数组，并在数组前头插入一个 $1$ 元素表示 $dp_{u,0}=1$ ，指根节点自己。

然后剩下的轻儿子的暴力向重儿子合并就可以了。时间复杂度 $O(2n)$ ，线性通过，因为每个子树节点的vector最多存放深度多个元素，总元素数虽多 $O(n)$ ，而不是暴力那样所有的全部开，没有的也开了。

关于直接继承重儿子信息，使用vector的swap函数显然比写指针更简单易懂。

#include<bits/stdc++.h>
#define int long long
using namespace std; 
const int N=1e6+5;
int n,x,y,cnt,hd[N],to[N<<1],nxt[N<<1],len[N],son[N],ans[N];
vector<int>f[N];    //这里的 vector 是倒序存储的，因为要在继承重儿子的信息后，要将当前节点的 DP 数组最前面插入一个元素，而 push_back 的复杂度优于 pop_front，倒序存储就可以直接使用 push_back 
void add(int x,int y){
    to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
}
int get(int x,int id){    //由于 vector 是倒序存储的，此处将 vector 正序存储的位置转化为倒序存储的位置 
    return len[x]-id-1;
}
void dfs1(int x,int fa){
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(y==fa) continue;
        dfs1(y,x);
        if(len[y]>len[son[x]]) son[x]=y;
    }
    len[x]=len[son[x]]+1;
}
void dfs2(int x,int fa){
    if(son[x]) dfs2(son[x],x),swap(f[x],f[son[x]]),ans[x]=ans[son[x]]+1;    //继承重儿子的信息。这里的继承直接用 swap 而不是复制，swap 在时间和空间上都更优（swap 交换 vector 的时间复杂度为 O(1)）。 
    f[x].push_back(1);    //push_back 的复杂度优于 pop_front
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(y==fa||y==son[x]) continue;
        dfs2(y,x);
        for(int j=1;j<=len[y];j++){
            f[x][get(x,j)]+=f[y][get(y,j-1)];    //暴力合并轻儿子的信息 
            if(f[x][get(x,j)]>f[x][get(x,ans[x])]||(f[x][get(x,j)]==f[x][get(x,ans[x])]&&j<ans[x])) ans[x]=j;    //更新答案
        }
    }
    if(f[x][get(x,ans[x])]==1) ans[x]=0;    //f[x][0]=1,f[x][ans[x]]=1，0 显然更优
}
signed main(){
    scanf("%lld",&n);
    for(int i=1;i<n;i++){
        scanf("%lld%lld",&x,&y);
        add(x,y),add(y,x);
    }
    dfs1(1,0),dfs2(1,0);
    for(int i=1;i<=n;i++)
        printf("%lld\n",ans[i]);
    return 0;
}

9. 动态树（LCT/Link-Cut Tree，实链剖分）

关键词：动态树，修改树结构后树上区间操作、序列化操作。

注意，序列上的跳跃同样可以视作一棵树来解决问题

维护一个森林，支持删除某条边，加入某条边，并保证加边，删边之后仍是森林。我们要维护这个森林的一些信息。

一般的操作有两点连通性，两点路径权值和，连接两点和切断某条边、修改信息等。

核心思想是我要谁我就把谁转到实链上面，其他的都是虚链。

$LCT$ 的辅助树性质：

辅助树由多棵 $Splay$ 组成，每棵 $Splay$ 维护原树中的一条路径，且中序遍历这棵 $Splay$ 得到的点序列，从前到后对应原树「从上到下」的一条路径。
原树每个节点与辅助树的 $Splay$ 节点一一对应。
辅助树的各棵 $Splay$ 之间并不是独立的。每棵 $Splay$ 的根节点的父亲节点本应是空，但在 $LCT$ 中每棵 $Splay$ 的根节点的父亲节点指向原树中 这条链 的父亲节点（即链最顶端的点的父亲节点）。这类父亲链接与通常 $Splay$ 的父亲链接区别在于儿子认父亲，而父亲不认儿子，对应原树的一条虚边。因此，每个连通块恰好有一个点的父亲节点为空。
由于辅助树的以上性质，我们维护任何操作都不需要维护原树，辅助树可以在任何情况下拿出一个唯一的原树，我们只需要维护辅助树即可。

示例：

给定 $n$ 个点以及每个点的权值，要你处理接下来的 $m$ 个操作。

操作有四种，操作从 $0$ 到 $3$ 编号。点从 $1$ 到 $n$ 编号。

0 x y 代表询问从 $x$ 到 $y$ 的路径上的点的权值的 $\text{xor}$ 和。保证 $x$ 到 $y$ 是联通的。
1 x y 代表连接 $x$ 到 $y$ ，若 $x$ 到 $y$ 已经联通则无需连接。
2 x y 代表删除边 $(x,y)$ ，不保证边 $(x,y)$ 存在。
3 x y 代表将点 $x$ 上的权值变成 $y$ 。

保证：

$1 \leq n \leq 10^5$ ， $1 \leq m \leq 3 \times 10^5$ ， $1 \leq a_i \leq 10^9$ 。
对于操作 $0, 1, 2$ ，保证 $1 \leq x, y \leq n$ 。
对于操作 $3$ ，保证 $1 \leq x \leq n$ ， $1 \leq y \leq 10^9$ 。

// LCT，动态树、实链剖分
#include <bits/stdc++.h>
using namespace std;
#define int long long
struct node
{
    int ch[2];
#define l ch[0]
#define r ch[1]
    int val = 0;
    int sum = 0;
    // int lazytag = 0;
    // int sz = 1;
    int revtag = 0;
    int fa = 0;
};
const int maxn = 5e5 + 9;
node tr[maxn];
void reverse(int x)
{
    tr[x].revtag ^= 1;
    return;
}
bool get(int x) // 获取x是父亲节点的哪个儿子
{
    return tr[tr[x].fa].r == x;
}
bool isroot(int x) // 判断x结点是否作为一棵动态Splay的根
{
    return tr[tr[x].fa].l != x && tr[tr[x].fa].r != x;
}
void pushup(int rt) // 更新结点信息
{
    // other pushups;
    // tr[rt].sz = tr[tr[rt].l].sz + tr[tr[rt].r].sz + 1;
    tr[rt].sum = tr[tr[rt].l].sum ^ tr[tr[rt].r].sum ^ tr[rt].val;
    return;
}
void pushdown(int x) // 树上懒标记，文艺平衡树标记是刚需求
{
    if (tr[x].revtag)
    {
        swap(tr[x].l, tr[x].r);
        if (tr[x].l)
            reverse(tr[x].l);
        if (tr[x].r)
            reverse(tr[x].r);
        tr[x].revtag = 0;
    }
}
void update(int x) // 动x之前结算x所在根的所有lazytag
{
    if (!isroot(x))
    {
        update(tr[x].fa);
    }
    pushdown(x);
    return;
}
void rotate(int x)
{
    int y = tr[x].fa, z = tr[y].fa, k = get(x);
    if (!isroot(y))
        tr[z].ch[tr[z].r == y] = x;
    // 上面这句一定要写在前面，普通的 Splay 是不用的，因为 isRoot  (后面会讲)
    tr[x].fa = z;
    tr[y].ch[k] = tr[x].ch[!k];
    tr[tr[x].ch[!k]].fa = y;
    tr[x].ch[!k] = y;
    tr[y].fa = x;
    pushup(y), pushup(x);
}
void Splay(int x) // 伸展操作，将结点伸展到根。
{
    update(x);
    for (int fa; fa = tr[x].fa, !isroot(x); rotate(x))
    {
        if (!isroot(fa))
            rotate(get(fa) == get(x) ? fa : x);
    }
}
int access(int x) // 拉直从x到当前动态树根节点的实边路径，返回该路径终点的Splay的根（即路径终点）
{
    int p;
    for (p = 0; x; p = x, x = tr[x].fa)
    {
        Splay(x);
        tr[x].r = p;
        pushup(x);
    }
    return p;
}
void makeroot(int x) // 换根操作，指定x结点成为原树（非辅助树）的总根
{
    access(x);  // 拉出x到当前根的路径，x必然是此时所在Splay中中序遍历的最后一个点
    Splay(x);   // 旋根，根据LCT-Splay定义，这棵Splay必定没有右儿子
    reverse(x); // 直接翻转Splay，迫使其成为当前Splay中序遍历第一个访问的点，成为深度最浅的根，实现了换跟
    return;
}
int find(int p) // 找结点p在原森林所属树（非辅助Splay森林树）的树根
{
    access(p);
    Splay(p);
    pushdown(p);
    while (tr[p].l)
        p = tr[p].l, pushdown(p);
    Splay(p);
    return p;
}
bool link(int x, int y) // 连一条x->y的轻边
{
    makeroot(x);
    if (find(y) == x)
        return 0;
    tr[x].fa = y;
    return 1;
}
bool cut(int x, int y)
{
    makeroot(x);
    if (find(y) != x || tr[y].fa != x || tr[y].l)
        return 0;
    tr[y].fa = tr[x].r = 0; // x在findroot(y)后被转到了根
    pushup(x);
    return 1;
}
void split(int x, int y) // 动态树中拆出来一条x->y指定路径，保证路径上都是实边,保证y在根。
{
    makeroot(x);
    access(y);
    Splay(y);
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        int v;
        cin >> v;
        tr[i].val = v;
        tr[i].sum = v;
    }
    while (m--)
    {
        int op, x, y;
        cin >> op >> x >> y;
        if (op == 0)
        {
            split(x, y);
            cout << tr[y].sum << endl;
        }
        else if (op == 1)
        {
            link(x, y);
        }
        else if (op == 2)
        {
            cut(x, y);
        }
        else
        {
            Splay(x); // 节点修改转到根再改，不会影响其他信息
            tr[x].val = y;
        }
    }
}

10. 01Trie

关于字典树Trie的内容，详见 $Part\ 2$ .

10.1 01Trie

01字典树。写法参见可持久化，没啥区别。

tr[rt].cnt存储的是从当前节点数位出发还有多少个数字，根节点就是数字的总个数。

10.2 可持久化01Trie

维护区间异或最大值或者区间第 $K$ 大值。区间第 $K$ 大值类似于主席树树上二分。

示例：（区间最大值）

给定一个非负整数序列 $\{a\}$ ，初始长度为 $N$ 。

有 $M$ 个操作，有以下两种操作类型：

A x：添加操作，表示在序列末尾添加一个数 $x$ ，序列的长度 $N$ 加 $1$ 。
Q l r x：询问操作，你需要找到一个位置 $p$ ，满足 $l \le p \le r$ ，使得： $a[p] \oplus a[p+1] \oplus ... \oplus a[N] \oplus x$ 最大，输出最大值。

对于所有测试点， $1\le N,M \le 3\times 10 ^ 5$ ， $0\leq a_i\leq 10 ^ 7$ 。

#include <bits/stdc++.h>
using namespace std;
struct Present_Trie
{
private:
    struct node
    {
        int nxt[2];
        int cnt = 0;
    };
    vector<node> tr;
    int tot = 0;
    int n;

public:
    void init(int n)
    {
        this->n = n;
        tr.resize(n << 5);
    }
    int newroot()
    {
        return ++tot;
    }
    void insert(int rt1, int rt2, int x)
    {
        for (int i = 30; i >= 0; i--)
        {
            int bit = (x >> i) & 1;
            if (bit)
            {
                if (!tr[rt2].nxt[1])
                {
                    tr[rt2].nxt[1] = ++tot;
                }
                tr[rt2].nxt[0] = tr[rt1].nxt[0];
                rt1 = tr[rt1].nxt[1];
                rt2 = tr[rt2].nxt[1];
            }
            else
            {
                if (!tr[rt2].nxt[0])
                {
                    tr[rt2].nxt[0] = ++tot;
                }
                tr[rt2].nxt[1] = tr[rt1].nxt[1];
                rt1 = tr[rt1].nxt[0];
                rt2 = tr[rt2].nxt[0];
            }
            tr[rt2].cnt = tr[rt1].cnt + 1;
        }
    }
    int query(int rt1, int rt2, int x)
    {
        int ret = 0;
        for (int i = 30; i >= 0; i--)
        {
            int bit = (x >> i) & 1;
            if (tr[tr[rt2].nxt[bit ^ 1]].cnt - tr[tr[rt1].nxt[bit ^ 1]].cnt > 0)
            {
                ret |= (1 << i);
                rt1 = tr[rt1].nxt[bit ^ 1];
                rt2 = tr[rt2].nxt[bit ^ 1];
            }
            else
            {
                rt1 = tr[rt1].nxt[bit];
                rt2 = tr[rt2].nxt[bit];
            }
        }
        return ret;
    }
};
Present_Trie pt;
int main()
{
    int n, q;
    cin >> n >> q;
    vector<int> root(n + 1);
    pt.init(1e6 + 9);
    int calc = 0;
    for (int i = 1; i <= n; i++)
    {
        int x;
        cin >> x;
        calc ^= x;
        root[i] = pt.newroot();
        pt.insert(root[i - 1], root[i], calc);
    }
    while (q--)
    {
        char c;
        int l, r, x;
        cin >> c;
        if (c == 'Q')
        {
            cin >> l >> r >> x;
            l--, r--;
            if (l == 0)
            {
                cout << max(x ^ calc, pt.query(root[l], root[r], x ^ calc)) << endl;
            }
            else
            {
                cout << pt.query(root[l - 1], root[r], x ^ calc) << endl;
            }
        }
        else if (c == 'A')
        {
            cin >> x;
            calc ^= x;
            root.emplace_back(pt.newroot());
            n++;
            pt.insert(root[n - 1], root[n], calc);
        }
    }
}

11.单调栈

单调栈，可以维护一个单调的序列，使得每一个元素进栈的时候，所有比这个元素小的栈内元素均会被其消除或者融合，比他大的栈内元素不会与其消除或者融合。最典型的例子就是维护某个数最左侧和最右侧第一个比其大的数。但是单调栈并不局限于此：

给定一个长度为 $m$ 的数组 $b$ 。您可以执行以下任意次操作（可能是零次）：

选择两个不同的索引 $i$ 和 $j$ ，其中 $\bf{1\le i < j\le m}$ 和 $b_i$ 为偶数，将 $b_i$ 除以 $2$ ，并将 $b_j$ 乘以 $2$ 。

您的任务是在执行任意数量的此类操作后最大化数组的总和。由于它可能很大，请输出此总和模数 $10^9+7$ 。

由于这道题太简单了，给你一个长度为 $n$ 的数组 $a$ ，你需要对 $a$ 的每个前缀进行求解。

换句话说，表示在执行任意数量的 $f(b)$ 等运算后 $b$ 的最大和，你需要分别输出 $f([a_1])$ 、 $f([a_1,a_2])$ 、 $\ldots$ 、 $f([a_1,a_2,\ldots,a_n])$ 模数 $10^9+7$ 。

不难考虑到每个数新加进序列的时候，所有比这个数小的底数（除尽2以后的数）所包含2的个数都要加到新数字上。很像一个线段树区间查，但是这会存在一个问题：

样例： 18 2 7

新加入的7显然查不到9底上的一个2，但是14可以查到。线段树最坏复杂度是 $nlog^2n$ 的。（实际上根据运算特性分析，能够卡满 $log^2n$ 单次询问的情况最多只有 $logn$ 次，所以真实实际复杂度为 $nlogn+log^3n\rightarrow nlogn$ 的复杂度）

所以，比当前数小的均可以合并，比当前数大的均无法合并，符合单调栈定义：

void solve()
{
    int n;
    cin >> n;
    mint tmpsum = 0;
    vector<i64> a(n + 1);
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    stack<pair<i64, i64>> st;
    for (int i = 1; i <= n; i++)
    {
        int k = 0;
        while (a[i] % 2 == 0)
        {
            k++;
            a[i] >>= 1;
        }
        while (!st.empty() && (k >= 30 || (a[i] << k) > st.top().first))
        {
            auto [num, cnt] = st.top();
            st.pop();
            tmpsum -= power(mint(2), cnt) * num;
            tmpsum += num;
            k += cnt;
        }
        st.push({a[i], k});
        tmpsum += mint(a[i]) * power(mint(2), k);
        cout << tmpsum << " ";
    }
    cout << endl;
    return;
}

Part 2. 数学

0. Modint.h

#ifndef __MODINT_H__

#define __MODINT_H__

using i64 = long long;

#include <bits/stdc++.h>

using namespace std;
namespace Modint
{
    template <class T>
    constexpr T power(T a, i64 b)
    {
        T res = 1;
        for (; b; b /= 2, a *= a)
        {
            if (b % 2)
            {
                res *= a;
            }
        }
        return res;
    }

    constexpr i64 mul(i64 a, i64 b, i64 p)
    {
        i64 res = a * b - (i64)(1.L * a * b / p) * p;
        res %= p;
        if (res < 0)
        {
            res += p;
        }
        return res;
    }
    /*
     * @brief 模运算（i64），jiangly版本，支持动态模数改变
     * @param P 模数，仅支持质数。如果选择动态定义模数，P=0，且必须调用setMod函数设置模数。默认为1e18+9
     */
    template <i64 P>
    struct MLong
    {
        i64 x;
        constexpr MLong() : x{} {}
        constexpr MLong(i64 x) : x{norm(x % getMod())} {}

        static i64 Mod;
        constexpr static i64 getMod()
        {
            if (P > 0)
            {
                return P;
            }
            else
            {
                return Mod;
            }
        }
        constexpr static void setMod(i64 Mod_)
        {
            Mod = Mod_;
        }
        constexpr i64 norm(i64 x) const
        {
            if (x < 0)
            {
                x += getMod();
            }
            if (x >= getMod())
            {
                x -= getMod();
            }
            return x;
        }
        constexpr i64 val() const
        {
            return x;
        }
        explicit constexpr operator i64() const
        {
            return x;
        }
        constexpr MLong operator-() const
        {
            MLong res;
            res.x = norm(getMod() - x);
            return res;
        }
        constexpr MLong inv() const
        {
            assert(x != 0);
            return power(*this, getMod() - 2);
        }
        constexpr MLong &operator*=(MLong rhs) &
        {
            x = mul(x, rhs.x, getMod());
            return *this;
        }
        constexpr MLong &operator+=(MLong rhs) &
        {
            x = norm(x + rhs.x);
            return *this;
        }
        constexpr MLong &operator-=(MLong rhs) &
        {
            x = norm(x - rhs.x);
            return *this;
        }
        constexpr MLong &operator/=(MLong rhs) &
        {
            return *this *= rhs.inv();
        }
        friend constexpr MLong operator*(MLong lhs, MLong rhs)
        {
            MLong res = lhs;
            res *= rhs;
            return res;
        }
        friend constexpr MLong operator+(MLong lhs, MLong rhs)
        {
            MLong res = lhs;
            res += rhs;
            return res;
        }
        friend constexpr MLong operator-(MLong lhs, MLong rhs)
        {
            MLong res = lhs;
            res -= rhs;
            return res;
        }
        friend constexpr MLong operator/(MLong lhs, MLong rhs)
        {
            MLong res = lhs;
            res /= rhs;
            return res;
        }
        friend constexpr std::istream &operator>>(std::istream &is, MLong &a)
        {
            i64 v;
            is >> v;
            a = MLong(v);
            return is;
        }
        friend constexpr std::ostream &operator<<(std::ostream &os, const MLong &a)
        {
            return os << a.val();
        }
        friend constexpr bool operator==(MLong lhs, MLong rhs)
        {
            return lhs.val() == rhs.val();
        }
        friend constexpr bool operator!=(MLong lhs, MLong rhs)
        {
            return lhs.val() != rhs.val();
        }
    };

    template <>
    i64 MLong<0LL>::Mod = (i64)(1E18) + 9;

    /*template <i64 V, i64 P>
    constexpr MLong<P> CInv = MLong<P>(V).inv();*/

    /*
     * @brief 模运算（int），jiangly版本，支持动态模数改变
     * @param P 模数，仅支持质数。如果选择动态定义模数，P=0，且必须调用setMod函数设置模数。默认为998244353
     */
    template <int P>
    struct MInt
    {
        int x;
        constexpr MInt() : x{} {}
        constexpr MInt(i64 x) : x{norm(x % getMod())} {}

        static int Mod;
        constexpr static int getMod()
        {
            if (P > 0)
            {
                return P;
            }
            else
            {
                return Mod;
            }
        }
        constexpr static void setMod(int Mod_)
        {
            Mod = Mod_;
        }
        constexpr int norm(int x) const
        {
            if (x < 0)
            {
                x += getMod();
            }
            if (x >= getMod())
            {
                x -= getMod();
            }
            return x;
        }
        constexpr int val() const
        {
            return x;
        }
        explicit constexpr operator int() const
        {
            return x;
        }
        constexpr MInt operator-() const
        {
            MInt res;
            res.x = norm(getMod() - x);
            return res;
        }
        constexpr MInt inv() const
        {
            assert(x != 0);
            return power(*this, getMod() - 2);
        }
        constexpr MInt &operator*=(MInt rhs) &
        {
            x = 1LL * x * rhs.x % getMod();
            return *this;
        }
        constexpr MInt &operator+=(MInt rhs) &
        {
            x = norm(x + rhs.x);
            return *this;
        }
        constexpr MInt &operator-=(MInt rhs) &
        {
            x = norm(x - rhs.x);
            return *this;
        }
        constexpr MInt &operator/=(MInt rhs) &
        {
            return *this *= rhs.inv();
        }
        friend constexpr MInt operator*(MInt lhs, MInt rhs)
        {
            MInt res = lhs;
            res *= rhs;
            return res;
        }
        friend constexpr MInt operator+(MInt lhs, MInt rhs)
        {
            MInt res = lhs;
            res += rhs;
            return res;
        }
        friend constexpr MInt operator-(MInt lhs, MInt rhs)
        {
            MInt res = lhs;
            res -= rhs;
            return res;
        }
        friend constexpr MInt operator/(MInt lhs, MInt rhs)
        {
            MInt res = lhs;
            res /= rhs;
            return res;
        }
        friend constexpr std::istream &operator>>(std::istream &is, MInt &a)
        {
            i64 v;
            is >> v;
            a = MInt(v);
            return is;
        }
        friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a)
        {
            return os << a.val();
        }
        friend constexpr bool operator==(MInt lhs, MInt rhs)
        {
            return lhs.val() == rhs.val();
        }
        friend constexpr bool operator!=(MInt lhs, MInt rhs)
        {
            return lhs.val() != rhs.val();
        }
    };

    template <>
    int MInt<0>::Mod = 998244353;

    // 逆元
    template <int V, int P>
    constexpr MInt<P> CInv = MInt<P>(V).inv();
    /*
     * @brief 阶乘类(适配Jiangly模板），支持计算组合数，排列数等操作，复杂度O(n),配套jiangly版本的模运算类
     * @brief 小数据时需要组合数建议使用组合数表（杨辉三角），大数据时需要组合数建议使用Lucas定理
     * @param MOD 模数，一般取质数，部分合数情况下可能没有逆元。
     * @note 支持计算组合数，可以使用C(n,k)计算组合数。
     * @note 支持计算排列数，可以使用A(n,k)计算排列数。
     */
    template <class T>
    struct Fact
    {
        std::vector<T> fact, factinv;
        const int n;
        Fact(const int &_n) : n(_n), fact(_n + 1, 1), factinv(_n + 1)
        {
            for (int i = 1; i <= n; ++i)
                fact[i] = fact[i - 1] * i;
            factinv[n] = fact[n].inv();
            for (int i = n; i; --i)
                factinv[i - 1] = factinv[i] * i;
        }
        T C(const int &n, const int &k)
        {
            if (n < 0 || k < 0 || n < k)
                return 0;
            return fact[n] * factinv[k] * factinv[n - k];
        }
        T A(const int &n, const int &k)
        {
            if (n < 0 || k < 0 || n < k)
                return 0;
            return fact[n] * factinv[n - k];
        }
    };
};

#endif //__MODINT_H__

1. 数论相关

1.1 大质数判定（Miller-Rabin素性测试）

以 $O(logN)$ 复杂度，以较高正确性判定质数。

#define i64 long long
    i64 mul(i64 a, i64 b, i64 m)
    {
        return static_cast<__int128>(a) * b % m;
    }
    i64 power(i64 a, i64 b, i64 m)
    {
        i64 res = 1 % m;
        for (; b; b >>= 1, a = mul(a, a, m))
            if (b & 1)
                res = mul(res, a, m);
        return res;
    }
    /* @brief Miller-Rabin 素性测试,时间复杂度为 O(log n)
     * @param n 待测试的数，不大于 1e18
     * @return true 为素数，false 为合数*/
    bool isprime(i64 n)
    {
        if (n < 2)
            return false;
        static constexpr int A[] = {2, 3, 5, 7, 11, 13, 17, 19, 23};
        int s = __builtin_ctzll(n - 1);
        i64 d = (n - 1) >> s;
        for (auto a : A)
        {
            if (a == n)
                return true;
            i64 x = power(a, d, n);
            if (x == 1 || x == n - 1)
                continue;
            bool ok = false;
            for (int i = 0; i < s - 1; ++i)
            {
                x = mul(x, x, n);
                if (x == n - 1)
                {
                    ok = true;
                    break;
                }
            }
            if (!ok)
                return false;
        }
        return true;
    }

1.2 质因数分解

1.2.1 小数字质因数分解

以 $O(N\sqrt N)$ 复杂度分解质因数。

vector<int> breakdown(int N) {
  vector<int> result;
  for (int i = 2; i * i <= N; i++) {
    if (N % i == 0) {  // 如果 i 能够整除 N，说明 i 为 N 的一个质因子。
      while (N % i == 0) N /= i;
      result.push_back(i);
    }
  }
  if (N != 1) {  // 说明再经过操作之后 N 留下了一个素数
    result.push_back(N);
  }
  return result;
}

1.2.2 大质数质因数分解（Pollar-Rho算法）

以期望复杂度 $O(N^{\frac{1}{4}})$ 复杂度分解质因数。

namespace Prime
{
using i64=long long;
    i64 mul(i64 a, i64 b, i64 m)
    {
        return static_cast<__int128>(a) * b % m;
    }
    i64 power(i64 a, i64 b, i64 m)
    {
        i64 res = 1 % m;
        for (; b; b >>= 1, a = mul(a, a, m))
            if (b & 1)
                res = mul(res, a, m);
        return res;
    }
    /* @brief Miller-Rabin 素性测试,时间复杂度为 O(log n)
     * @param n 待测试的数，不大于 1e18
     * @return true 为素数，false 为合数
     */
    bool isprime(i64 n)
    {
        if (n < 2)
            return false;
        static constexpr int A[] = {2, 3, 5, 7, 11, 13, 17, 19, 23};
        int s = __builtin_ctzll(n - 1);
        i64 d = (n - 1) >> s;
        for (auto a : A)
        {
            if (a == n)
                return true;
            i64 x = power(a, d, n);
            if (x == 1 || x == n - 1)
                continue;
            bool ok = false;
            for (int i = 0; i < s - 1; ++i)
            {
                x = mul(x, x, n);
                if (x == n - 1)
                {
                    ok = true;
                    break;
                }
            }
            if (!ok)
                return false;
        }
        return true;
    }
    /* @brief 素因子分解（Pollard-Rho 算法）,时间复杂度期望为 O(n^(1/4))，最坏为 O(n^(1/2))，本函数复杂度带排序，具体复杂度待定，可估算为亚线性
     * @param n 待分解的数，不大于 1e18
     * @return 一个 vector，包含了 n 的所有素因子，按照从小到大的顺序排列，包括重复的
     */
    std::vector<i64> factorize(i64 n)
    {
        std::vector<i64> p;
        std::function<void(i64)> f = [&](i64 n)
        {
            if (n <= 10000)
            {
                for (int i = 2; i * i <= n; ++i)
                    for (; n % i == 0; n /= i)
                        p.push_back(i);
                if (n > 1)
                    p.push_back(n);
                return;
            }
            if (isprime(n))
            {
                p.push_back(n);
                return;
            }
            auto g = [&](i64 x)
            {
                return (mul(x, x, n) + 1) % n;
            };
            i64 x0 = 2;
            while (true)
            {
                i64 x = x0;
                i64 y = x0;
                i64 d = 1;
                i64 power = 1, lam = 0;
                i64 v = 1;
                while (d == 1)
                {
                    y = g(y);
                    ++lam;
                    v = mul(v, std::abs(x - y), n);
                    if (lam % 127 == 0)
                    {
                        d = std::gcd(v, n);
                        v = 1;
                    }

                    if (power == lam)
                    {
                        x = y;
                        power *= 2;
                        lam = 0;
                        d = std::gcd(v, n);
                        v = 1;
                    }
                }
                if (d != n)
                {
                    f(d);
                    f(n / d);
                    return;
                }
                ++x0;
            }
        };
        f(n);
        std::sort(p.begin(), p.end());
        return p;
    }
    /*
     * @brief 素因子分解（Pollard-Rho 算法）
     * @param n 待分解的数，不大于 1e18
     * @return 一个 vector，包含了 n 的所有素因子，按照从小到大的顺序排列，first 为素因子，second 为指数
     */
    std::vector<std::pair<i64, i64>> factorize_pairs(i64 n)
    {
        std::vector<i64> p = factorize(n);
        std::vector<std::pair<i64, i64>> res;
        for (auto i : p)
        {
            if (res.empty() || res.back().first != i)
                res.emplace_back(i, 1);
            else
                res.back().second++;
        }
        return res;
    }
    void dfs(int p, i64 n, std::vector<std::pair<i64, i64>> &ps, std::vector<i64> &ds)
    {
        if (p == ps.size())
        {
            if (n > 1)
            {
                ds.push_back(n);
            }
            return;
        }
        for (i64 i = 0; i <= ps[p].second; i++)
        {
            dfs(p + 1, n, ps, ds);
            n *= ps[p].first;
        }
        return;
    }
    /*
     * @brief 因数集合(不含1,Pollard-Rho 算法质因数分解)
     * @param n 待考察的数，不大于 1e18
     * @return 一个 vector，包含了 n 的因子，按照从小到大的顺序排列。不含1。
     */
    std::vector<i64> getd(i64 n)
    {
        std::vector<std::pair<i64, i64>> p = factorize_pairs(n);
        std::vector<i64> d;
        dfs(0, 1, p, d);
        std::sort(d.begin(), d.end());
        return d;
    }

};

1.3 基于值域处理的快速GCD

你需要解决以下问题：

以 $O(1)$ 的单次询问复杂度、 $O(n)$ 的总时间复杂度回答 $\forall x,y\in[1,n],gcd(x,y)=?$

操作方法：

将任意 $x$ 分解成三个数的乘积 $a\times b\times c$ ，则显然 $a,b,c\le \sqrt n$ .

考虑线筛，若 $x$ 为质数，显然 $(1,1,x)$ 它的一个分解；

若 $x$ 为合数，设 $p$ 是 $x$ 的最小质因子， $(a_0,b_0,c_0)$ 是 $\frac{x}{p}$ 的一个分解；

则显然有 $(a_0p,b_0,c_0)$ 排序后是一个从小到大的分解。

若求 $gcd(x,y)$ ，设 $x=a\times b\times c$ . 勒令 $p_1=y,r_1=gcd(a,p_1)$ .

勒令 $p_2=\frac{p_1}{r_1}$ ， $r_2=gcd(b,p_2)$ ； $p_3=\frac{p_2}{r_2}$ ， $r_3=gcd(c,p_3)$ .

则有 $gcd(x,y)=r_1r_2r_3.$

原理为 $gcd(x,y)=rgcd(x/r,y/r)\quad iff\quad r|x,r|y$

#include <bits/stdc++.h>
using namespace std;
const int INF = 1e6 + 1;
const int maxn = 5001;
vector<array<int, 3>> v(INF + 10);
bool vis[INF + 10];
int prime[INF + 10];
void euler()
{
    v[1] = {1, 1, 1};
    for (int i = 2; i <= INF; i++)
    {
        if (!vis[i])
        {
            vis[i] = 1;
            prime[++prime[0]] = i;
            v[i] = {1, 1, i};
        }
        for (int j = 1; j <= prime[0] && i * prime[j] <= INF; j++)
        {
            int k = i * prime[j];
            vis[k] = 1;
            v[k] = {v[i][0] * prime[j], v[i][1], v[i][2]};
            sort(v[k].begin(), v[k].end());
            if (i % prime[j] == 0)
                break;
        }
    }
}
int gcds[1010][1010];
void init()
{
    gcds[0][0] = 0;
    for (int i = 1; i <= 1000; i++)
    {
        gcds[i][0] = gcds[0][i] = i;
        for (int j = 1; j <= i; j++)
        {
            gcds[i][j] = gcds[j][i] = gcds[j][i % j];
        }
    }
}
int Gcd(int a, int b)
{
    int ret = 1;
    for (int i = 0, r; i < 3; i++)
    {
        if (v[a][i] > 1e3)
        {
            if (b % v[a][i])
                r = 1;
            else
                r = v[a][i];
        }
        else
            r = gcds[v[a][i]][b % v[a][i]];
        b /= r;
        ret = ret * r;
    }
    return ret;
}

1.4 扩展欧几里得定理

可求出方程 $ax+by=gcd(a,b)$ 的一组特解。该方程通解为：

$\left\{ \begin{aligned} x=x^{'}+k\frac{b}{gcd(a,b)}&\\ \\&,k\in Z\\ y=y^{'}-k\frac{a}{gcd(a,b)}\\ \end{aligned} \right.$

取最小的非负解，x=(x%s+s)%s。

void exgcd(int a, int b, int &x, int &y)
{
    if (b == 0)
    {
        x = 1, y = 0;
        return;
    }
    exgcd(b, a % b, y, x);
    y -= (a / b) * x;
}

1.5 积性函数线性筛（欧拉函数筛）

如果一个积性函数能够满足以下三条性质：

$f(p)可O(1)查询$
若 $gcd(n,m)=1$ ，则 $\varphi(nm)=\varphi(n)\varphi(m)$
若 $n\mid m$ ,则 $\varphi(nm)可积性转移$ （即递推公式只含有乘法）

则均可使用线性筛实现线性求解。

筛法求欧拉函数：

int prime[maxn];
bool vis[maxn];//初始0，标记合数
int phi[maxn];
void euler(int n)
{
    for(int i=2;i<=n;i++)
    {
        if(!vis[i])prime[++prime[0]]=i,phi[i]=i-1;\\性质1
        for(int j=1;j<=prime[0]&&i*prime[j]<=n;j++)
        {
            vis[i*prime[j]]=true;\\筛去合数
            if(i%prime[j]==0)
            {
                phi[i*prime[j]]=prime[j]*phi[i];\\性质3
                break;
            }
            phi[i*prime[j]]=phi[prime[j]]*phi[i];\\性质2
        }
    }
}

因数个数筛：

struct pre
{
    int n;
    vector<int> d;
    vector<int> num;
    vector<bool> vis;
    vector<int> prime;
    void init(int _n)
    {
        n = _n;
        d.resize(n + 1);
        num.resize(n + 1);
        vis.resize(n + 1);
    }
    void did()
    {
        d[1] = 1;
        for (int i = 2; i <= n; i++)
        {
            if (!vis[i])
            {
                prime.push_back(i);
                d[i] = 2;
                num[i] = 1;
            }
            for (int j = 0; j < prime.size() && i * prime[j] <= n; j++)
            {
                vis[i * prime[j]] = 1;
                if (i % prime[j] == 0)
                {
                    num[i * prime[j]] = num[i] + 1;
                    d[i * prime[j]] = d[i] / (num[i * prime[j]]) * (num[i * prime[j]] + 1);
                    break;
                }
                num[i * prime[j]] = 1;
                d[i * prime[j]] = d[i] * 2;
            }
        }
    }
    int qs(int x)
    {
        return d[x];
    }
};

若函数 $f(n)$ 满足 $f(1)=1$ 且 $\forall x,y\in N^*,gcd(x,y)=1$ 都有 $f(xy)=f(x)f(y)$ ，则 $f(n)$ 为积性函数。

特别的，若 $\forall x,y\in N^*$ 都有 $f(xy)=f(x)f(y)$ ,则称作完全积性函数。

若 $f(x)$ 和 $g(x)$ 均为积性函数，那么下列函数也称作积性函数：

$\begin{align} &h(x)=f(x^p)\\ &h(x)=f^p(x)\\ &h(x)=f(x)g(x)\\ &h(x)=\sum_{d\mid x}f(d)g(\frac{x}{d})\\ \end{align}$

设质因数分解 $x=\prod_{i=1}^{n}p_i^{k_i}$ ，则

若 $F(x)$ 为积性函数，则 $F(x)=\prod_{i=1}^{n}f(p_i^k)$

若 $F(x)$ 为完全积性函数，则 $F(x)=\prod_{i=1}^{n}f(p_i^k)=\prod_{i=1}^{n}f^k(p_i)$

（因为质数和其自己的 $gcd$ 并不是1而是其本身）

常见积性函数:

欧拉函数 $\varphi(n)=\sum_{i=1}^{n}[gcd(i,n)=1]$ .
除数函数 $\sigma_k(n)=\sum_{d\mid n}d^k,k\in N.$

（特别的， $\sigma_0(n)$ 又记作 $d(n)$ ，表示除数的个数。 $\sigma_1(n)$ 又记作 $\sigma(n)$ ，表示因数和）

二者均为非完全积性函数。

莫比乌斯函数

$\begin{align}\mu(n)=\left\{ \begin{aligned} &\quad \ -1\qquad \quad \ \ iff\ \ n\ is\ a\ prime \\ &\qquad 0\qquad \qquad n^{'}\;mod\;p1=0\\ &-\mu(n^{'})\qquad \quad otherwise \end{aligned} \right. &,n=p_1\cdot n^{'} \end{align}$

欧拉函数 $\varphi(n)=\sum_{i=1}^{n}[gcd(i,n)=1]$

通解公式

$\varphi(x)=x\prod_{i=1}^{n}(1-\frac{1}{p_i})\,\,\,\,,\,\,\,x=\prod_{i=1}^{n}p_i^{k_i}$

性质

$\varphi(p)=p-1$
$\varphi(p^k)=p^{k-1}\varphi(p)$
若 $gcd(n,m)=1$ ，则 $\varphi(nm)=\varphi(n)\varphi(m)$
若 $n\mid m$ ,则 $\varphi(nm)=n\varphi(m)$

仔细观察不难发现2是4的子集关系，故性质1、3、4称作欧拉函数三性质，简称欧拉函数性。

1.6 裴蜀定理

$\begin{aligned} &设不全为0的整数a,b，对于任意整数x,y有\\ \\ &\qquad gcd(a,b)|(ax+by)\\ \\ &且一定存在整数解x_0,y_0使得下列方程成立\\ \\ &\qquad ax_0+by_0=gcd(a,b) \end{aligned}$

上述情形可以推广到任意多变量。

1.7 扩展欧拉定理

$a^b\equiv \left \{ \begin{aligned} &a^{b\ mod\ \varphi(m)}\qquad \qquad gcd(a,m)=1\\ &a^b \qquad\qquad\qquad\quad\ gcd(a,m)\neq1,b<\varphi(m)\\ &a^{(b\ mod\ \varphi(m))+\varphi(m)} \quad \ gcd(a,m)\neq1,b\geq\varphi(m) \end{aligned} \right.\quad (mod\ m)$

1.8 乘法逆元

线性逆元：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
int mod;
const int maxn = 6e6 + 9;
int inv[maxn];
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int a;
    cin >> a >> mod;
    inv[1] = 1;
    cout << 1 << endl;
    for (int i = 2; i <= a; i++)
    {
        inv[i] = (mod - mod / i) * inv[mod % i] % mod;
        cout << inv[i] << endl;
    }
}

快速幂逆元（费马小定理）：

$对于任意正整数a，\exists p满足gcd(a,p)=1,则必然有以下同余式成立:\\ a^{p-1} \equiv1\ (mod \; n)$

1	quickpow(a,mod-2);

1.9 中国剩余定理

给定 $n$ 组非负整数 $a_i, b_i$ ，求解关于 $x$ 的方程组的最小非负整数解。

$\begin{cases}x\equiv b_1\pmod{a_1}\\x\equiv b_2\pmod{a_2}\\\dots\\x\equiv b_n\pmod{a_n}\end{cases}$

对于 $100 \%$ 的数据， $1 \le n \le {10}^5$ ， $1 \le b_i,a_i \le {10}^{12}$ ，保证所有 $a_i$ 的最小公倍数不超过 ${10}^{18}$ 。不保证 $b$ 为质数

请注意程序运行过程中进行乘法运算时结果可能有溢出的风险。

#include <bits/stdc++.h>
using namespace std;
#define int long long
int quickmul(int a, int b, int mod)
{
    while (a < 0)
        a += mod;
    while (b < 0)
        b += mod;
    if (a < b)
        swap(a, b);
    int e = 0;
    while (b)
    {
        if (b & 1)
            (e += a) %= mod;
        (a <<= 1) %= mod;
        b >>= 1;
    }
    return e;
}
void exgcd(int a, int b, int &x, int &y)
{
    if (b == 0)
    {
        x = 1, y = 0;
        return;
    }
    exgcd(b, a % b, y, x);
    y -= (a / b) * x;
}
const int maxn = 500001;
int a[maxn], m[maxn]; // 对m取模余数是a
int n;
int ExCRT()
{
    int mod = m[1], ans = a[1];
    for (int i = 2; i <= n; i++)
    {
        int b1 = mod, b2 = m[i], c = __gcd(b1, b2), minus = (a[i] - ans % b2 + b2) % b2;
        if (minus % c != 0)
            return -1;
        b1 /= c, b2 /= c, minus /= c;
        int x, y;
        exgcd(b1, b2, x, y);
        x = quickmul(x, minus, b2);
        ans += x * mod;
        mod *= b2;
        ans = (ans % mod + mod) % mod;
    }
    return ans;
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> m[i] >> a[i];
    }
    cout << ExCRT() << endl;
    return 0;
}

1.10 离散对数

1.10.1 原根

满足 $a^n\equiv 1\ (mod \ m),gcd(a,m)=1$ 的最小正整数 $n$ 存在，称 $n$ 为 $a$ 的阶，记作 $\delta_m(a)$ 。

给定 $m$ ，若 $gcd(g,m)=1$ 且 $\delta_m(g)=\varphi(m)$ ，则称 $g$ 为 $m$ 的一个原根（循环群的生成元）。

详细见 $OI-Wiki$

1.10.2 离散对数

定义 $a^x\equiv b\ (mod\ m)$ ， $a$ 为 $m$ 的一个原根时，记 $x=ind_ab$ ，称作 $b$ 关于 $m$ 的离散对数。

1.10.3 ExBSGS算法

给定 $a,p,b$ ，求满足 $a^x≡b \pmod p$ 的最小自然数 $x$ 。如果无解，输出 No Solution，否则输出最小自然数解。

对于 $100\%$ 的数据， $1\le a,p,b≤10^9$ 或 $a=p=b=0$ 。 $\sum \sqrt p\le 5\times 10^6$ 。

原理：搞到和BSGS算法一致，通过 $a \equiv b \ (mod\ c) \iff a\times d\equiv b\times d\ (mod\ c\times d)$

每次在两边除以 $d=gcd(a,p)$ ，得到 $\frac{a}{d}\times a^{x-1}\equiv\frac{b}{d}\ (mod\ \frac{p}{d})$

重复执行该语段，直到 $gcd(a,p)=1$ 为止。

然后上 $BSGS$ 根号暴力分治算，复杂度 $O(\sqrt {\varphi(p)})$

#include <bits/stdc++.h>
using namespace std;
inline int BSGS(int a, int n, int p, int ad = 1) // ad*(a^x)=n(mod p)
{
    unordered_map<int, int> mp;
    int m = ceil(sqrt(p));
    int s = 1;
    for (int i = 0; i < m; i++, s = 1ll * s * a % p)
        mp[1ll * s * n % p] = i;
    for (int i = 0, tmp = s, s = ad; i <= m; i++, s = 1ll * s * tmp % p)
        if (mp.find(s) != mp.end())
            if (1ll * i * m - mp[s] >= 0)
                return 1ll * i * m - mp[s];
    return -1;
}
inline int exBSGS(int a, int n, int p)
{
    a %= p;
    n %= p;
    if (n == 1 || p == 1)
        return 0;
    int cnt = 0;
    int d, ad = 1;
    while ((d = gcd(a, p)) ^ 1)
    {
        if (n % d)
            return -1;
        cnt++;
        n /= d;
        p /= d;
        ad = (1ll * ad * a / d) % p;
        if (ad == n)
            return cnt;
    }
    int ans = BSGS(a, n, p, ad);
    if (ans == -1)
        return -1;
    return ans + cnt;
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int a, p, n;
    while (cin >> a >> p >> n)
    {
        if (!a && !p && !n)
            break;
        int ans = exBSGS(a, n, p);
        if (~ans)
            cout << ans << "\n";
        else
            cout << "No Solution" << "\n";
    }
    return 0;
}

1.11 二次剩余（奇素数）

给出 $N,p$ ，求解方程

$x^2 \equiv N \pmod{p}$

多组数据，且保证 $p$ 是奇素数。

输出共 $T$ 行。

对于每一行输出，若有解，则按 $\bmod ~p$ 后递增的顺序输出在 $\bmod~ p$ 意义下的全部解；若两解相同，只输出其中一个；若无解，则输出 Hola! 。

对于 $100\%$ 的数据， $1\leq T\leq 10^4,0\le N, p\leq 10^9+9$ 。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
random_device rd;
mt19937 ran(rd());
struct num
{
    ll x; // 实部
    ll y; // 虚部(即虚数单位√w的系数)
};

ll t, w, n, p;

num mul(num a, num b, ll p)
{ // 复数乘法
    num res;
    res.x = ((a.x * b.x % p + a.y * b.y % p * w % p) % p + p) % p; // x = a.x*b.x + a.y*b.y*w
    res.y = ((a.x * b.y % p + a.y * b.x % p) % p + p) % p;         // y = a.x*b.y + a.y*b.x
    return res;
}
ll qpow_r(ll a, ll b, ll p)
{ // 实数快速幂
    ll res = 1;
    while (b)
    {
        if (b & 1)
            res = res * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return res;
}
ll qpow_i(num a, ll b, ll p)
{ // 复数快速幂
    num res = {1, 0};
    while (b)
    {
        if (b & 1)
            res = mul(res, a, p);
        a = mul(a, a, p);
        b >>= 1;
    }
    return res.x % p; // 只用返回实数部分，因为虚数部分没了
}
ll cipolla(ll n, ll p)
{
    n %= p;
    if (qpow_r(n, (p - 1) / 2, p) == -1 + p)
        return -1; // 据欧拉准则判定是否有解
    ll a;
    while (1)
    { // 找出一个符合条件的a
        a = ran() % p;
        w = (((a * a) % p - n) % p + p) % p; // w = a^2 - n，虚数单位的平方
        if (qpow_r(w, (p - 1) / 2, p) == -1 + p)
            break;
    }
    num x = {a, 1};
    return qpow_i(x, (p + 1) / 2, p);
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t;
    cin >> t;
    while (t--)
    {
        cin >> n >> p;
        if (!n)
        {
            cout << 0 << "\n";
            continue;
        }
        ll ans1 = cipolla(n, p), ans2 = -ans1 + p; // 另一个解就是其相反数
        if (ans1 == -1)
            cout << "Hola!\n";
        else
        {
            if (ans1 > ans2)
                swap(ans1, ans2);
            if (ans1 == ans2)
                cout << ans1 << "\n";
            else
                cout << ans1 << " " << ans2 << "\n";
        }
    }
    return 0;
}

1.12 数论分块

以期望复杂度 $O(\sqrt x)$ 的复杂度求解 $F(x)=\sum_{i=1}^ng(\lfloor\frac{x}i\rfloor)$ 。

分块理论：如果 $\lfloor\frac{x}{i}\rfloor=\lfloor\frac{x}{j}\rfloor$ ，则有该块的分块区间为 $\large [i,\lfloor\frac{x}{\lfloor\frac{x}{i}\rfloor}\rfloor]$

原理： $\lfloor\frac{x}{ab}\rfloor=\lfloor\frac{\lfloor\frac{x}{a}\rfloor}{b}\rfloor$

long long H(int n) {
  long long res = 0;  // 储存结果
  int l = 1, r;       // 块左端点与右端点
  while (l <= n) {
    r = n / (n / l);  // 计算当前块的右端点
    // 累加这一块的贡献到结果中。乘上 1LL 防止溢出
    res += 1LL * (r - l + 1) * (n / l);
    l = r + 1;  // 左端点移到下一块
  }
  return res;
}

如果是向上取整分块 $F(x)=\sum_{i=1}^ng(\lceil\frac{x}i\rceil)$ ，则有如果 $\lceil\frac{x}{i}\rceil=\lceil\frac{x}{j}\rceil$ ，则有该块的分块区间为 $\large [i,\lceil\frac{x}{\lceil\frac{x-1}{i}\rceil}\rceil]$ 。注意特殊处理 $i\ge x$ 的情况，此时分块右端点分母为 $0$ .注意右边界的写法。

auto calc = [&](auto self, int x) -> i64
    {
        if (mp.count(x))
            return mp[x];
        i64 res = 0;
        int i = 2;
        while (i <= n)
        {
            int invr = (x - 1) / i;
            int r = n;
            if (invr != 0)                  // 分块防0
                r = min(r, (x - 1) / invr); // 注意分块值域不要超过你求和式的上界
            res = (res + (r - i + 1) * self(self, (x + i - 1) / i) % mod) % mod;
            i = r + 1;
        }
        res = (res * inv) % mod;
        res = (res + n * inv % mod) % mod;
        return mp[x] = res;
    };

2. 线性代数相关

2.1 矩阵快速幂

#include <bits/stdc++.h>
using namespace std;
#include <icpc-model/Modint.h>
using namespace Modint;
const int mod = 1e9 + 7;
using mint = MInt<mod>;
vector<vector<mint>> operator*(vector<vector<mint>> a, vector<vector<mint>> b)
{
    vector<vector<mint>> c(a.size(), vector<mint>(a.size(), 0));
    int n = a.size();
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            for (int k = 0; k < n; k++)
            {
                c[i][j] += (a[i][k] * b[k][j]);
            }
        }
    }
    return c;
}
void solve()
{
    int n;
    long long k;
    cin >> n >> k;
    vector<vector<mint>> E(n, vector<mint>(n, 0));
    vector<vector<mint>> A = E;
    for (int i = 0; i < n; i++)
        E[i][i] = 1;
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            cin >> A[i][j];
        }
    }
    while (k)
    {
        if (k & 1)
            E = E * A;
        A = A * A;
        k >>= 1;
    }
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            cout << E[i][j] << " ";
        }
        cout << endl;
    }
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t;
    // cin >> t;
    // while (t--)
    solve();
}

2.2 矩阵数列递推

对数列递推式子列矩阵方程就行。最著名的就是feibonacci数列：

\pmatrix{f_n\\f_{n-1}} =\pmatrix{1\ 1\\1 \ 0}\pmatrix{f_{ n-1}\\f_{n-2}}

2.3 矩阵求逆/高斯消元(仅可求唯一解)

求矩阵的逆矩阵，无解判定矩阵非满秩矩阵，等价于解线性方程组。使用高斯消元法即可。

#include <bits/stdc++.h>
using namespace std;
const int mod = 998244353;
#define endl '\n'
const int P = 1e9 + 7;
int power(int a, int b, int mod)
{
    int res = 1;
    while (b)
    {
        if (b & 1)
            res = (1ll * res * a) % mod;
        a = (1ll * a * a) % mod;
        b >>= 1;
    }
    return res % mod;
}
std::vector<int> gauss(std::vector<std::vector<int>> a, std::vector<int> b)
{
    int n = a.size();
    for (int i = 0; i < n; ++i)
    {
        int r = i;
        while (a[r][i] == 0)
            ++r;
        std::swap(a[i], a[r]);
        std::swap(b[i], b[r]);
        int inv = power(a[i][i], P - 2, P);
        for (int j = i; j < n; ++j)
            a[i][j] = 1ll * a[i][j] * inv % P;
        b[i] = 1ll * b[i] * inv % P;
        for (int j = 0; j < n; ++j)
        {
            if (i == j)
                continue;
            int x = a[j][i];
            for (int k = i; k < n; ++k)
                a[j][k] = (a[j][k] + 1ll * (P - x) * a[i][k]) % P;
            b[j] = (b[j] + 1ll * (P - x) * b[i]) % P;
        }
    }
    return b;
}
/**   高斯消元法（gaussian elimination）【久远】
 *    2020-12-02: https://www.codechef.com/viewsolution/39942900
 **/
std::vector<double> gauss(std::vector<std::vector<double>> a, std::vector<double> b, int &rank)
{
    int n = a.size();
    for (int i = 0; i < n; ++i)
    {
        int r = i;
        while (r < n && a[r][i] == 0)
            ++r;
        if (r == n)
            return b;
        std::swap(a[i], a[r]);
        std::swap(b[i], b[r]);
        double x = a[i][i];
        rank++;
        for (int j = i; j < n; ++j)
            a[i][j] /= x;
        b[i] /= x;
        for (int j = 0; j < n; ++j)
        {
            if (i == j)
                continue;
            x = a[j][i];
            for (int k = i; k < n; ++k)
                a[j][k] -= a[i][k] * x;
            b[j] -= b[i] * x;
        }
    }
    return b;
}
vector<vector<int>> invmatrix(vector<vector<int>> a, vector<vector<int>> b, int &rank)
{
    int n = a.size();
    for (int i = 0; i < n; ++i)
    {
        int r = i;
        while (r < n && a[r][i] == 0)
            ++r;
        if (r == n)
            break;
        rank++;
        swap(a[i], a[r]);
        swap(b[i], b[r]);
        int inv = power(a[i][i], P - 2, P);
        for (int j = i; j < n; ++j)
            a[i][j] = 1ll * a[i][j] * inv % P;
        for (int k = 0; k < n; k++)
            b[i][k] = 1ll * b[i][k] * inv % P;
        for (int j = 0; j < n; ++j)
        {
            if (i == j)
                continue;
            int x = a[j][i];
            for (int k = i; k < n; ++k)
                a[j][k] = (a[j][k] + 1ll * (P - x) * a[i][k]) % P;
            for (int k = 0; k < n; k++)
                b[j][k] = (b[j][k] + 1ll * (P - x) * b[i][k]) % P;
        }
    }
    return b;
}

void solve()
{
    int n;
    cin >> n;
    vector<vector<int>> a(n, vector<int>(n));
    vector<vector<int>> E(n, vector<int>(n));
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            cin >> a[i][j];
            if (i == j)
                E[i][j] = 1;
        }
    }
    vector<vector<int>> A;
    int rk = 0;
    A = invmatrix(a, E, rk);
    if (rk != n)
    {
        cout << "No Solution" << endl;
        return;
    }

    for (auto &i : A)
    {
        for (auto &j : i)
        {
            cout << j << " ";
        }
        cout << endl;
    }
}

signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    // int t;
    // cin >> t;
    // while (t--)
    solve();
}

2.4 线性基

不难发现，按位Bitwise Xor运算是一个针对MOD2剩余系向量空间加法运算，故存在代数线性基。

线性空间 $<Z_2^n,bitwise\ Xor,bitwise\ And>$ 为域空间。

我们可以利用异或线性基实现：

判断一个数能否表示成某数集子集的异或和（已有集合元素是否能够构造出0）；
求一个数表示成某数集子集异或和的方案数；
求某数集子集的最大/最小/第 $k$ 大/第 $k$ 小异或和；

如果说，线性基中异或的最大数（的二进制形式）是一串 连续的，没有带后续 $0$ 的 $1$ ，那相信聪明的你一定会求第 $k$ 大，因为第 $k$ 大其实就是 $k$ 。

现在相当于告诉你在这一串 $1$ 中夹了很多 $0$ ，问你第 $k$ 大是多少。那么你其实可以不用管中间的 $0$ ，把 $k$ 的二进制形式弄出来，然后把中间省略 $0$ 给插回去就好了。（因为最大值位是 $0$ 的地方一辈子不可能出 $1$ ）
解释一下就相当于把线性基异或后出来的最大值里的所有 $1$ 都给挤到最后，然后求出第 $k$ 大，再把你弄走的0给丢回去。

$eg:$ 异或后最大值为 $101100110_2$ ，问第 $20$ 大

挤到后面去后成 $11111_2$ ，第 $k$ 大是 $10100_2$ ，把 $0$ 插回去成为 $100100000_2$ ，第20大便是 $100100000_2$
求一个数在某数集子集异或和中的排名。

线性基的独立性决定了一组异或为0的数无论以什么顺序插入最终线性基都不会允许这n个数同时插入线性基中，所以和线性基相关的贪心直接对权值排序后按顺序插入线性基就可以了。

注意，线性基的插入是可重复贡献的，所以支持树上倍增 $RMQ$ ，思想参考树上倍增lca查询和序列区间最大值查询。线性基的极大无关性保证任意一组线性基最多是 $logn$ 级别的，支持暴力合并。可以借助树上倍增实现树上查询问题。

求 $x\rightarrow y$ 路径上的最大异或和，只需要四段彩色弧线段所代表的倍增线性基合并即可，这是 $O(log^2n)$ 的单次询问。求 $lca$ 方式的倍增跳是 $O(log^3n)$ 的。

struct LineBase
{
private:
    const static int MN = 62;
    i64 a[MN + 1], tmp[MN + 1];
    bool flag; // 线性基中是否有重复插入的元素

public:
    void insert(i64 x)
    {
        for (int i = MN; ~i; i--)
            if (x & (1ll << i))
                if (!a[i])
                {
                    a[i] = x;
                    return;
                }
                else
                    x ^= a[i];
        flag = true;
    }
    bool check(i64 x) // 查看当前线性基中能否表示出来这个数(是否已插入)
    {
        for (int i = MN; ~i; i--)
            if (x & (1ll << i))
                if (!a[i])
                    return false;
                else
                    x ^= a[i];
        return true;
    }
    i64 qmax(i64 res = 0)
    {
        for (int i = MN; ~i; i--)
            res = max(res, res ^ a[i]);
        return res;
    }
    i64 qmin()
    {
        if (flag) // 线性基有试图插入过相同的数，最小值为0
            return 0;
        for (int i = 0; i <= MN; i++)
            if (a[i])
                return a[i];
    }
    i64 query(i64 k) // 线性基下第k小
    {
        i64 res = 0;
        int cnt = 0;
        k -= flag; // 线性基有试图插入过相同的数，最小值为0
        if (!k)
            return 0;
        for (int i = 0; i <= MN; i++)
        {
            for (int j = i - 1; ~j; j--)
                if (a[i] & (1ll << j))
                    a[i] ^= a[j];
            if (a[i])
                tmp[cnt++] = a[i];
        } // 线性基重构
        if (k >= (1ll << cnt))
            return -1;
        for (int i = 0; i < cnt; i++)
            if (k & (1ll << i))
                res ^= tmp[i];
        return res;
    }
};
LineBase lb;

树上倍增查询路径max

#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
using u64 = unsigned long long;
const i64 mod = 998244353;
#define endl '\n'
struct LineBase
{
private:
    const static int MN = 60;
    array<u64, MN + 1> a;
    bool flag;
    friend LineBase merge(LineBase a, LineBase b);

public:
    LineBase()
    {
        a.fill(0);
    }
    void ins(u64 x)
    {
        for (int i = MN; ~i; i--)
            if (x & (1ll << i))
                if (!a[i])
                {
                    a[i] = x;
                    return;
                }
                else
                    x ^= a[i];
        flag = true;
    }
    bool check(u64 x)
    {
        for (int i = MN; ~i; i--)
            if (x & (1ll << i))
                if (!a[i])
                    return false;
                else
                    x ^= a[i];
        return true;
    }
    u64 qmax(u64 res = 0)
    {
        for (int i = MN; ~i; i--)
            res = max(res, res ^ a[i]);
        return res;
    }
    u64 qmin()
    {
        if (flag)
            return 0;
        for (int i = 0; i <= MN; i++)
            if (a[i])
                return a[i];
    }

    void merge(LineBase b)
    {
        for (int i = 0; i < b.MN; i++)
        {
            this->ins(b.a[i]);
        }
    }
};
LineBase merge(LineBase a, LineBase b)
{
    LineBase c = a;
    for (int i = 0; i < b.MN; i++)
    {
        c.ins(b.a[i]);
    }
    return c;
}
struct node
{
    int fa;
    LineBase lb;
};
const int maxn = 2e4 + 9;
node st[maxn][16];
vector<int> con[maxn];
vector<int> dep;
vector<u64> num;
void add_edge(int u, int v)
{
    con[u].push_back(v);
    con[v].push_back(u);
}
void dfs(int u, int fa)
{
    st[u][0].fa = fa;
    dep[u] = dep[fa] + 1;
    st[u][0].lb.ins(num[u]);
    st[u][0].lb.ins(num[fa]);
    for (int j = 1; j <= 15; j++)
    {
        st[u][j].fa = st[st[u][j - 1].fa][j - 1].fa;
        st[u][j].lb = merge(st[u][j - 1].lb, st[st[u][j - 1].fa][j - 1].lb);
    }
    for (auto v : con[u])
    {
        if (v == fa)
            continue;
        dfs(v, u);
    }
    return;
}
pair<int, LineBase> lca(int u, int v)
{
    if (dep[u] < dep[v])
        swap(u, v);
    int tmp = dep[u] - dep[v];
    LineBase ans;
    ans.ins(num[u]), ans.ins(num[v]);
    for (int j = 0; j <= 15; j++)
    {
        if ((tmp >> j) & 1)
            ans.merge(st[u][j].lb), u = st[u][j].fa;
    }
    if (u == v)
        return {u, ans};
    for (int j = 15; j >= 0; j--)
    {
        if (st[u][j].fa != st[v][j].fa)
        {
            ans.merge(st[u][j].lb);
            ans.merge(st[v][j].lb);
            u = st[u][j].fa, v = st[v][j].fa;
        }
    }
    ans.merge(st[u][0].lb);
    ans.merge(st[v][0].lb);
    return {st[u][0].fa, ans};
}

void solve()
{
    int n, q;
    cin >> n >> q;
    num.assign(n + 1, 0);
    dep.assign(n + 1, 0);
    for (int i = 1; i <= n; i++)
    {
        cin >> num[i];
    }
    for (int i = 1; i < n; i++)
    {
        int u, v;
        cin >> u >> v;
        add_edge(u, v);
    }
    dfs(1, 1);
    while (q--)
    {
        int u, v;
        cin >> u >> v;
        cout << lca(u, v).second.qmax() << endl;
    }
}

signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
    // cin >> t;
    while (t--)
        solve();
}

2.5 二进制矩阵类Matrix.h

这段代码定义了一个名为 matrix_Z2_base 的模板类，它用于表示和操作 $<Z_2^n,xor,and>$ 线性空间的矩阵。元素只有0和1，运算在 $mod2$ 数域下。

构造函数：
- matrix_Z2_base(int n, int m, bool init_diagonal = false, bool init_off_diagonal = false)：创建一个大小为 n×m 的矩阵，其中 n 是行数，m 是列数。init_diagonal 和 init_off_diagonal 参数用于初始化对角线和非对角线元素。如果 init_diagonal 为 true，则对角线元素被初始化为 1，否则为 0。非对角线元素的初始化由 init_off_diagonal 控制。
访问操作符：
- std::bitset<SZ> &operator[](int i)：返回第 i 行的引用。
- const std::bitset<SZ> &operator[](int i) const：返回第 i 行的常量引用。
切片操作：
- matrix_Z2_base &inplace_slice(int il, int ir, int jl, int jr)：在原地修改矩阵，返回左上角为 (il, jl)，右下角为 (ir, jr) 的子矩阵。
- matrix_Z2_base slice(int il, int ir, int jl, int jr) const：返回左上角为 (il, jl)，右下角为 (ir, jr) 的子矩阵的副本。
行切片和列切片：
- matrix_Z2_base &inplace_row_slice(int il, int ir)：在原地修改矩阵，返回行切片子矩阵。
- matrix_Z2_base row_slice(int il, int ir) const：返回行切片子矩阵的副本。
- matrix_Z2_base &inplace_column_slice(int jl, int jr)：在原地修改矩阵，返回列切片子矩阵。
- matrix_Z2_base column_slice(int jl, int jr) const：返回列切片子矩阵的副本。
比较操作符：
- bool operator==(const matrix_Z2_base &a) const：比较两个矩阵是否相等。
- bool operator!=(const matrix_Z2_base &a) const：比较两个矩阵是否不相等。
矩阵加法和减法：
- matrix_Z2_base &operator+=(const matrix_Z2_base &M)：原地矩阵加法。
- matrix_Z2_base operator+(const matrix_Z2_base &M) const：返回两个矩阵相加的结果。
- matrix_Z2_base &operator-=(const matrix_Z2_base &M)：原地矩阵减法。
- matrix_Z2_base operator-(const matrix_Z2_base &M) const：返回两个矩阵相减的结果。
矩阵乘法：
- matrix_Z2_base &operator*=(const matrix_Z2_base &a)：原地矩阵乘法。
- matrix_Z2_base operator*(const matrix_Z2_base &a) const：返回两个矩阵相乘的结果。
矩阵乘以常数：
- matrix_Z2_base &operator*=(bool c)：将矩阵的每个元素乘以布尔常数 c。
- matrix_Z2_base operator*(bool c) const：返回乘以常数后的矩阵。
矩阵乘方：
- matrix_Z2_base &inplace_power(T e)：原地计算矩阵的 e 次幂。
- matrix_Z2_base power(T e) const：返回矩阵的 e 次幂。
矩阵转置：
- matrix_Z2_base &inplace_transpose()：原地转置矩阵。
- matrix_Z2_base transpose() const：返回矩阵的转置。
矩阵乘以行向量：
- std::vector<int> operator*(const std::bitset<SZ> &v) const：将矩阵乘以行向量 v。
行阶梯形式和行列式、秩：
- tuple<matrix_Z2_base &, bool, int> inplace_REF(int up_to = -1)：原地计算矩阵的行阶梯形式，并返回行列式和秩。
- tuple<matrix_Z2_base, bool, int> REF(int up_to = -1) const：返回矩阵的行阶梯形式，并返回行列式和秩。
矩阵逆：
- optional<matrix_Z2_base> inverse() const：返回矩阵的逆，如果矩阵不可逆，则返回空。
行列式：
- bool determinant() const：返回矩阵的行列式是否为 1。
秩：
- int rank() const：返回矩阵的秩。

线性方程组的解：

optional<std::bitset<SZ>> find_a_solution() const：返回矩阵所代表的线性方程组的一个解。

解多解 $n$ 元 $n$ 式线性方程组示例：

for (auto s = 0; s < n; ++s)
{
    matrix_Z2 M(n + 1, n + 1);//第n行表示主元都有谁，第n列是方程增广列，表示各线性方程结果。
    for (auto u = 0; u < n; ++u)
    {
        for (auto v = 0; v < n; ++v)
        {
            if (adjm[u] >> v & 1)
            {
                M[v][u] = 1;//原题是个图论，根据边列的矩阵方程
            }
        }
        M[n][u] = u == s;//标记主元，表示第s个元素的解必须是1，给出来的多组解必定线性无关
    }
    M[n][n] = 1;
    if (auto resptr = M.find_a_solution())
    {
        auto pick = *resptr;
        for (auto u = 0; u < n; ++u)
        {
            if (pick[u])
            {
                res[u] |= 1LL << s;
            }
        }
    }
    else
    {
        cout << "No\n";
        return 0;
    }
}

输出操作符：
- friend output_stream &operator<<(output_stream &out, const matrix_Z2_base &a)：输出矩阵到流。
矩阵乘以常数（外部）：
- matrix_Z2_base<SZ> operator*(bool c, matrix_Z2_base<SZ> M)：返回乘以常数后的矩阵。
行向量乘以矩阵：
- std::bitset<SZ> operator*(const std::vector<int> &v, const matrix_Z2_base<SZ> &a)：将行向量 v 乘以矩阵 a。

#ifndef __MATRIX_H__
#define __MATRIX_H__
#include <bits/stdc++.h>
using namespace std;
/*
 *@brief 二进制矩阵类
 *@note 该类支持矩阵的加减乘，求逆，求行列式，求秩，求行阶梯形式，求解线性方程组等操作
 *@tparam SZ 矩阵列向量的位数，即矩阵的列数，用于初始化bitset的位数
 */
template <size_t SZ>
struct matrix_Z2_base
{
    int n, m;
    std::vector<std::bitset<SZ>> data;
    std::bitset<SZ> &operator[](int i)
    {
        assert(0 <= i && i < n);
        return data[i];
    }
    const std::bitset<SZ> &operator[](int i) const
    {
        assert(0 <= i && i < n);
        return data[i];
    }
    matrix_Z2_base &inplace_slice(int il, int ir, int jl, int jr)
    {
        assert(0 <= il && il <= ir && ir <= n);
        assert(0 <= jl && jl <= jr && jr <= m);
        n = ir - il, m = jr - jl;
        if (il > 0)
            for (auto i = 0; i < n; ++i)
                swap(data[i], data[il + i]);
        data.resize(n);
        for (auto &row : data)
            row = row << SZ - jr >> jl;
        return *this;
    }
    /*
     *@brief 返回一个子矩阵
     *@param il 左上角行坐标
     *@param ir 右下角行坐标
     *@param jl 左上角列坐标
     *@param jr 右下角列坐标
     *@return 返回一个子矩阵
     */
    matrix_Z2_base slice(int il, int ir, int jl, int jr) const
    {
        return matrix_Z2_base(*this).inplace_slice(il, ir, jl, jr);
    }
    matrix_Z2_base &inplace_row_slice(int il, int ir)
    {
        assert(0 <= il && il <= ir && ir <= n);
        n = ir - il;
        if (il > 0)
            for (auto i = 0; i < n; ++i)
                swap(data[i], data[il + i]);
        data.resize(n);
        return *this;
    }
    /*
     *@brief 返回一个行切片子矩阵
     *@param il 左上角行坐标
     *@param ir 右下角行坐标
     *@return 返回一个行切片子矩阵
     */
    matrix_Z2_base row_slice(int il, int ir) const
    {
        return matrix_Z2_base(*this).inplace_row_slice(il, ir);
    }
    matrix_Z2_base &inplace_column_slice(int jl, int jr)
    {
        assert(0 <= jl && jl <= jr && jr <= m);
        m = jr - jl;
        for (auto &row : data)
            row = row << SZ - jr >> jl;
        return *this;
    }
    /*
     *@brief 返回一个列切片子矩阵
     *@param jl 左上角列坐标
     *@param jr 右下角列坐标
     *@return 返回一个列切片子矩阵
     */
    matrix_Z2_base column_slice(int jl, int jr) const
    {
        return matrix_Z2_base(*this).inplace_column_slice(jl, jr);
    }
    // 矩阵相等
    bool operator==(const matrix_Z2_base &a) const
    {
        assert(n == a.n && m == a.m);
        return data == a.data;
    }
    // 矩阵不等
    bool operator!=(const matrix_Z2_base &a) const
    {
        assert(n == a.n && m == a.m);
        return data != a.data;
    }
    // 矩阵相加
    matrix_Z2_base &operator+=(const matrix_Z2_base &M)
    {
        assert(n == M.n && m == M.m);
        for (auto i = 0; i < n; ++i)
            data[i] ^= M[i];
        return *this;
    }
    // 矩阵相加
    matrix_Z2_base operator+(const matrix_Z2_base &M) const
    {
        return matrix_Z2_base(*this) += M;
    }
    // 矩阵相减
    matrix_Z2_base &operator-=(const matrix_Z2_base &M)
    {
        assert(n == M.n && m == M.m);
        for (auto i = 0; i < n; ++i)
            data[i] ^= M[i];
        return *this;
    }
    // 矩阵相减
    matrix_Z2_base operator-(const matrix_Z2_base &M) const
    {
        return matrix_Z2_base(*this) -= M;
    }
    // 矩阵相乘
    matrix_Z2_base &operator*=(const matrix_Z2_base &a)
    {
        assert(m == a.n);
        int l = a.m;
        matrix_Z2_base res(n, l);
        std::vector<std::bitset<SZ>> temp(l);
        for (auto i = 0; i < l; ++i)
            for (auto j = 0; j < m; ++j)
                temp[i][j] = a[j][i];
        for (auto i = 0; i < n; ++i)
            for (auto j = 0; j < l; ++j)
                res[i][j] = (data[i] & temp[j]).count() & 1;
        return *this = res;
    }
    // 矩阵相乘
    matrix_Z2_base operator*(const matrix_Z2_base &a) const
    {
        return matrix_Z2_base(*this) *= a;
    }
    // 矩阵乘以一个常数
    matrix_Z2_base &operator*=(bool c)
    {
        if (!c)
            for (auto &v : *this)
                v.reset();
        return *this;
    }
    // 矩阵乘以一个常数
    matrix_Z2_base operator*(bool c) const
    {
        return matrix_Z2_base(*this) *= c;
    }
    // 矩阵乘方
    template <class T, typename enable_if<is_integral<T>::value>::type * = nullptr>
    matrix_Z2_base &inplace_power(T e)
    {
        assert(n == m);
        matrix_Z2_base res(n, n, true);
        for (; e; *this *= *this, e >>= 1)
            if (e & 1)
                res *= *this;
        return *this = res;
    }
    // 矩阵乘方
    template <class T>
    matrix_Z2_base power(T e) const
    {
        return matrix_Z2_base(*this).inplace_power(e);
    }
    // 矩阵转置
    matrix_Z2_base &inplace_transpose()
    {
        assert(n == m);
        for (auto i = 0; i < n; ++i)
            for (auto j = i + 1; j < n; ++j)
                swap(data[i][j], data[j][i]);
        return *this;
    }
    // 矩阵转置
    matrix_Z2_base transpose() const
    {
        if (n == m)
            return matrix_Z2_base(*this).inplace_transpose();
        matrix_Z2_base res(m, n);
        for (auto i = 0; i < n; ++i)
            for (auto j = 0; j < m; ++j)
                res[j][i] = data[i][j];
        return res;
    }
    /*
     *@brief 矩阵乘以一个行向量
     *@param v 行向量
     *@return 返回一个行向量
     *@note 行向量必须在矩阵左乘，时间复杂度O(n * m / w)
     */
    std::vector<int> operator*(const std::bitset<SZ> &v) const
    {
        std::vector<int> res(n);
        for (auto i = 0; i < n; ++i)
            res[i] = (data[i] & v).count() & 1;
        return res;
    }
    // O(n * m * up_to / w)
    // Returns {REF matrix, determinant, rank}

    /*
     *@brief 矩阵的行阶梯形式
     *@param up_to 行阶梯形式的行数，带参数的情况下只计算前up_to=m-1列向量的行阶梯形式，用于解线性方程组
     *@return 返回一个元组，第一个元素是行阶梯形式的矩阵，第二个元素是行列式，第三个元素是秩
     *@note 时间复杂度O(n * m * up_to / w),如果要解多解线性方程组，如果想固定第k个自由变量，需要对传入矩阵的a_{n,k}置1,同时增广向量的对应位a_{n,n}也必须置1，然后调用该函数。
     *@note 实际上等价于新添了一组线性方程，即a_{n,k} * x_k = a_{n,n}。
     */
    tuple<matrix_Z2_base &, bool, int> inplace_REF(int up_to = -1)
    {
        if (n == 0)
            return {*this, true, 0};
        if (!~up_to)
            up_to = m;
        bool det = true;
        int rank = 0;
        for (auto j = 0; j < up_to; ++j)
        {
            int pivot = -1;
            for (auto i = rank; i < n; ++i)
                if (data[i][j])
                {
                    pivot = i;
                    break;
                }
            if (!~pivot)
            {
                det = false;
                continue;
            }
            if (rank != pivot)
                swap(data[rank], data[pivot]);
            for (auto i = rank + 1; i < n; ++i)
                if (data[i][j])
                    data[i] ^= data[rank];
            ++rank;
            if (rank == n)
                break;
        }
        return {*this, det, rank};
    }
    // O(n * m * up_to / w)
    // Returns {REF matrix, determinant, rank}
    /*
     *@brief 矩阵的行阶梯形式
     *@param up_to 行阶梯形式的行数
     *@return 返回一个元组，第一个元素是行阶梯形式的矩阵，第二个元素是行列式，第三个元素是秩
     *@note 时间复杂度O(n * m * up_to / w)。解多解线性方程组时，如果想固定第k个自由变量，需要对传入矩阵的a_{n,k}置1,同时增广向量的对应位a_{n,n}也必须置1，然后调用该函数。
     *@note 实际上等价于新添了一组线性方程，即a_{n,k} * x_k = a_{n,n}。
     */
    tuple<matrix_Z2_base, bool, int> REF(int up_to = -1) const
    {
        return matrix_Z2_base(*this).inplace_REF(up_to);
    }
    // O(n * m * min(n, m) / w)
    /*
     *@brief 矩阵的逆
     *@return 返回一个可选的矩阵，表示矩阵的逆
     */
    optional<matrix_Z2_base> inverse() const
    {
        assert(n == m);
        std::vector<std::bitset<SZ>> a(data), res(n);
        for (auto i = 0; i < n; ++i)
            res[i].set(i);
        for (auto j = 0; j < n; ++j)
        {
            int pivot = -1;
            for (auto i = j; i < n; ++i)
                if (a[i][j])
                {
                    pivot = i;
                    break;
                }
            if (!~pivot)
                return {};
            swap(a[j], a[pivot]), swap(res[j], res[pivot]);
            for (auto i = 0; i < n; ++i)
                if (i != j && a[i][j])
                    a[i] ^= a[j], res[i] ^= res[j];
        }
        swap(*this, res);
        return true;
    }
    /*
     *@brief 矩阵的行列式
     *@return 返回一个布尔值，表示矩阵的行列式是否为1
     */
    bool determinant() const
    {
        assert(n == m);
        matrix_Z2_base a(data);
        for (auto i = 0; i < n; ++i)
        {
            for (auto j = i + 1; j < n; ++j)
                if (a[j][i])
                {
                    if (a[i][i])
                        a[j] ^= a[i];
                    else
                        swap(a[i], a[j]);
                }
            if (!a[i][i])
                return false;
        }
        return true;
    }
    // O(n^3 / w)
    /*
     *@brief 矩阵的秩
     *@return 返回一个整数，表示矩阵的秩
     *@note 时间复杂度O(n^3 / w)
     */
    int rank() const
    {
        return get<2>(REF());
    }
    // Regarding the matrix as a system of linear equations by separating first m-1 columns, find a solution of the linear equation.
    // O(n * m^2 / w)
    /*
     *@brief 矩阵所代表的线性方程组的一个解
     *@return 返回一个可选的位集，表示矩阵的一个解
     *@note 时间复杂度O(n * m^2 / w),该矩阵所代表的线性方程组系数矩阵为低m-1位，常数项为第m位，表示n*(m-1)的增广矩阵。
     *@note 时间复杂度O(n * m * up_to / w),如果要解多解线性方程组，如果想固定第k个自由变量，需要对传入矩阵的a_{n,k}置1,同时增广向量的对应位a_{n,n}也必须置1，然后调用该函数。
     *@note 实际上等价于新添了一组线性方程，即a_{n,k} * x_k = a_{n,n}。
     */
    optional<std::bitset<SZ>> find_a_solution() const
    {
        assert(m >= 1);
        auto [ref, _, rank] = REF(m - 1);
        for (auto i = rank; i < n; ++i)
            if (ref[i][m - 1])
                return {};
        std::bitset<SZ> res;
        for (auto i = rank - 1; i >= 0; --i)
        {
            int pivot = ref[i]._Find_first();
            assert(pivot < m - 1);
            res[pivot] = ref[i][m - 1] ^ (ref[i] & res).count() & 1;
        }
        return res;
    }
    template <class output_stream>
    friend output_stream &operator<<(output_stream &out, const matrix_Z2_base &a)
    {
        out << "\n";
        for (auto i = 0; i < a.n; ++i)
        {
            for (auto j = 0; j < a.m; ++j)
                out << bool(a[i][j]);
            out << "\n";
        }
        return out;
    }
    /*
     *@brief 构造函数
     *@param n 行数
     *@param m 列数
     *@param init_diagonal 对角线是否初始化
     *@param init_off_diagonal 非对角线是否初始化
     */
    matrix_Z2_base(int n, int m, bool init_diagonal = false, bool init_off_diagonal = false) : n(n), m(m), data(n)
    {
        assert(m <= SZ);
        for (auto i = 0; i < n; ++i)
            for (auto j = 0; j < m; ++j)
                data[i][j] = i == j ? init_diagonal : init_off_diagonal;
    }
    /*
     *@brief 构造函数
     *@param n 行数
     *@param m 列数
     *@param a 矩阵
     */
    matrix_Z2_base(int n, int m, const std::vector<std::bitset<SZ>> &a) : n(n), m(m), data(a) {}
};
/*
 *@brief 矩阵乘以一个常数
 *@param c 常数
 *@param M 矩阵
 *@return 返回一个矩阵
 */
template <size_t SZ>
matrix_Z2_base<SZ> operator*(bool c, matrix_Z2_base<SZ> M)
{
    if (!c)
        for (auto &v : M)
            v.reset();
    return M;
}
// Multiply a row std::vector v on the left
/*
 *@brief 行向量乘以矩阵
 *@param v 行向量
 *@param a 矩阵
 *@return 返回一个行向量
 */
template <size_t SZ>
std::bitset<SZ> operator*(const std::vector<int> &v, const matrix_Z2_base<SZ> &a)
{
    assert(a.n == (int)v.size());
    std::bitset<SZ> res;
    for (auto i = 0; i < a.n; ++i)
        if (v[i])
            res ^= a[i];
    return res;
}

#endif

3. 多项式相关

关键词：卷积优化。动态规划优化。

3.1 快速傅里叶变换（FTT）/多项式乘法

给定一个 $n$ 次多项式 $F(x)$ ，和一个 $m$ 次多项式 $G(x)$ 。

请求出 $F(x)$ 和 $G(x)$ 的卷积，从低次方项到高次方项给出系数。

保证输入中的系数大于等于 $0$ 且小于等于 $9$ 。

对于 $100\%$ 的数据： $1 \le n, m \leq {10}^6$ 。

$FTT$ 等下列一系列快速变换的本质都是选择出来 $2^w=n$ 个多项式点值，用这组点值向量的运算去替代多项式的运算。

#include <bits/stdc++.h>
#include <math.h>
using namespace std;
using d32 = double;
#define endl '\n'
const d32 PI = 3.14159265358979323846;
void fft(vector<complex<d32>> &a)
{
    int n = a.size();
    if (n == 1)
        return;
    vector<complex<d32>> a0(n / 2), a1(n / 2);
    for (int i = 0; i < n / 2; i++)
    {
        a0[i] = a[i * 2];
        a1[i] = a[i * 2 + 1];
    }
    fft(a0);
    fft(a1);
    d32 ang = 2 * PI / n;
    complex<d32> w(1), wn(cos(ang), sin(ang));
    for (int i = 0; i < n / 2; i++)
    {
        a[i] = a0[i] + w * a1[i];
        a[i + n / 2] = a0[i] - w * a1[i];
        w *= wn;
    }
}
vector<d32> mul(vector<d32> a, vector<d32> b)
{
    int n = 1;
    while (n < a.size() + b.size())
        n *= 2;
    a.resize(n);
    b.resize(n);
    vector<complex<d32>> A(a.begin(), a.end()), B(b.begin(), b.end());
    fft(A);
    fft(B);
    for (int i = 0; i < n; i++)
        A[i] *= B[i];
    for (int i = 0; i < n; i++)
        A[i] = conj(A[i]);//逆变换前求倒数。
    fft(A);
    vector<d32> res(n);
    for (int i = 0; i < n; i++)
        res[i] = round(A[i].real() / n);
    return res;
}
void solve()
{
    int n, m;
    cin >> n >> m;
    vector<d32> a(n + 1), b(m + 1);
    for (int i = 0; i <= n; i++)
        cin >> a[i];
    for (int i = 0; i <= m; i++)
        cin >> b[i];
    vector<d32> res = mul(a, b);
    for (int i = 0; i <= n + m; i++)
        cout << (long long)res[i] << " ";
    cout << endl;
}

signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
    // cin >> t;
    while (t--)
        solve();
}

还有一种写法：

using d32 = double;
#define endl '\n'
const d32 PI = 3.14159265358979323846;
void fft(vector<complex<double>> &f, int op)
{
    int n = f.size();
    if (n == 1)
        return;
    vector<complex<double>> f0(n / 2), f1(n / 2);
    for (int i = 0; i < n / 2; i++)
    {
        f0[i] = f[i * 2];
        f1[i] = f[i * 2 + 1];
    }
    fft(f0, op);
    fft(f1, op);
    complex<double> cur(1, 0), step(cos(2 * PI / n), sin(2 * PI * op / n));
    for (int k = 0; k < n / 2; ++k)
    {
        complex<double> tmp = cur * f1[k];
        f[k] = f0[k] + tmp;
        f[k + n / 2] = f0[k] - tmp;
        cur *= step;
    }
    return;
}
vector<d32> mul(vector<d32> &a, vector<d32> &b)
{
    int n = 1;
    while (n < a.size() + b.size())
        n *= 2;
    a.resize(n);
    b.resize(n);
    vector<complex<d32>> A(a.begin(), a.end()), B(b.begin(), b.end());
    fft(A, 1);
    fft(B, 1);
    for (int i = 0; i < n; i++)
        A[i] *= B[i];
    fft(A, -1);
    vector<d32> res(n);
    for (int i = 0; i < n; i++)
        res[i] = round(A[i].real() / n);
    return res;
}

3.2 快速数论变换（NTT）/多项式乘法

constexpr int P = 998244353;

int power(int a, int b)
{
    int res = 1;
    for (; b; b /= 2, a = 1LL * a * a % P)
    {
        if (b % 2)
        {
            res = 1LL * res * a % P;
        }
    }
    return res;
}

std::vector<int> rev, roots{0, 1};

void dft(std::vector<int> &a)
{
    int n = a.size();
    if (int(rev.size()) != n)
    {
        int k = __builtin_ctz(n) - 1;
        rev.resize(n);
        for (int i = 0; i < n; i++)
        {
            rev[i] = rev[i >> 1] >> 1 | (i & 1) << k;
        }
    }
    for (int i = 0; i < n; i++)
    {
        if (rev[i] < i)
        {
            std::swap(a[i], a[rev[i]]);
        }
    }
    if (roots.size() < n)
    {
        int k = __builtin_ctz(roots.size());
        roots.resize(n);
        while ((1 << k) < n)
        {
            int e = power(31, 1 << (__builtin_ctz(P - 1) - k - 1));
            for (int i = 1 << (k - 1); i < (1 << k); i++)
            {
                roots[2 * i] = roots[i];
                roots[2 * i + 1] = 1LL * roots[i] * e % P;
            }
            k++;
        }
    }

    for (int k = 1; k < n; k *= 2)
    {
        for (int i = 0; i < n; i += 2 * k)
        {
            for (int j = 0; j < k; j++)
            {
                int u = a[i + j];
                int v = 1LL * a[i + j + k] * roots[k + j] % P;
                a[i + j] = (u + v) % P;
                a[i + j + k] = (u - v + P) % P;
            }
        }
    }
}

void idft(std::vector<int> &a)
{
    int n = a.size();
    std::reverse(a.begin() + 1, a.end());
    dft(a);
    int inv = power(n, P - 2);
    for (int i = 0; i < n; i++)
    {
        a[i] = 1LL * a[i] * inv % P;
    }
}

std::vector<int> mul(std::vector<int> a, std::vector<int> b)
{
    int n = 1, tot = a.size() + b.size() - 1;
    while (n < tot)
    {
        n *= 2;
    }
    if (tot < 128)
    {
        std::vector<int> c(a.size() + b.size() - 1);
        for (int i = 0; i < a.size(); i++)
        {
            for (int j = 0; j < b.size(); j++)
            {
                c[i + j] = (c[i + j] + 1LL * a[i] * b[j]) % P;
            }
        }
        return c;
    }
    a.resize(n);
    b.resize(n);
    dft(a);
    dft(b);
    for (int i = 0; i < n; i++)
    {
        a[i] = 1LL * a[i] * b[i] % P;
    }
    idft(a);
    a.resize(tot);
    return a;
}

3.3 快速莫比乌斯变换/快速沃尔什变换（FMT/FWT）

给定长度为 $2^n$ 两个序列 $A,B$ ，设

$C_i=\sum_{j\oplus k = i}A_j \times B_k$

分别当 $\oplus$ 是 $or, and, xor$ 时求出 $C$ 。称作或、与、异或卷积。请区分他们与对应乘法的区别。

卷积原理： $FMT$ 是子集运算， $FWT$ 是 $x\circ y=popcount(x\&y)\%2$

$FMT_{and}(A)_i=\sum_{i\&j=i}a_j$

$FMT_{or}(A)_i=\sum_{i|j=i}a_j$

$FMT_{xor}(A)_i=\sum_{i\circ j=0}a_j-\sum_{i\circ j=1}a_j$

注意，针对异或的快速沃尔什变换是线性变换的，即 $FWT(c\cdot A+B)=c\cdot FWT(A)+FWT(B)$

对数组 $F(x)=x^0$ （即只有 $a[0]=1$ ，其余位置全为 $0$ ）的快速 $FWT$ 后所得序列全为 $1$ 。

对数组 $F(x)=x^t$ （即只有 $a[t]=1$ ，其余位置全为 $0$ ）的快速 $FWT$ 后所得序列全为 $1$ 或者 $-1$ （显然）

std::vector<int> fwt_and(vector<int> a)
{
    int n = a.size();
    for (int i = 1; i < n; i <<= 1)
        for (int j = 0; j < n; j += i << 1)
            for (int k = 0; k < i; k++)
                a[j + k] = (1ll * a[j + k] + a[i + j + k]) % mod;
    return a;
}
std::vector<int> ifwt_and(vector<int> a)
{
    int n = a.size();
    for (int i = 1; i < n; i <<= 1)
        for (int j = 0; j < n; j += i << 1)
            for (int k = 0; k < i; k++)
                a[j + k] = (1ll * a[j + k] - a[i + j + k] + mod) % mod;
    return a;
}
std::vector<int> fwt_or(vector<int> a)
{
    int n = a.size();
    for (int i = 1; i < n; i <<= 1)
        for (int j = 0; j < n; j += i << 1)
            for (int k = 0; k < i; k++)
                a[i + j + k] = (1ll * a[j + k] + a[i + j + k]) % mod;
    return a;
}
std::vector<int> ifwt_or(vector<int> a)
{
    int n = a.size();
    for (int i = 1; i < n; i <<= 1)
        for (int j = 0; j < n; j += i << 1)
            for (int k = 0; k < i; k++)
                a[i + j + k] = (1ll * a[i + j + k] - a[j + k] + mod) % mod;
    return a;
}
std::vector<int> fwt_xor(vector<int> a) // 异或
{
    int n = a.size();
    for (int i = 1; i < n; i <<= 1)
        for (int j = 0; j < n; j += i << 1)
            for (int k = 0; k < i; k++)
            {
                int x = a[j + k], y = a[i + j + k];
                a[j + k] = (1ll * x + y) % mod;
                a[i + j + k] = (1ll * x - y + mod) % mod;
            }
    return a;
}
std::vector<int> ifwt_xor(vector<int> a)
{
    int inv_2 = 499122177;
    int n = a.size();
    for (int i = 1; i < n; i <<= 1)
        for (int j = 0; j < n; j += i << 1)
            for (int k = 0; k < i; k++)
            {
                int x = a[j + k], y = a[i + j + k];
                a[j + k] = (1ll * x + y) * inv_2 % mod;
                a[i + j + k] = (1ll * x - y + mod) % mod * inv_2 % mod;
            }
    return a;
}

std::vector<int> fwt_not(std::vector<int> a) // 同或
{
    int n = a.size();
    for (int i = 1; i < n; i <<= 1)
        for (int j = 0; j < n; j += i << 1)
            for (int k = 0; k < i; k++)
            {
                int x = a[j + k], y = a[i + j + k];
                a[i + j + k] = (1ll * x + y) % mod;
                a[j + k] = (1ll * x - y + mod) % mod;
            }
    return a;
}
std::vector<int> ifwt_not(std::vector<int> a)
{
    int inv_2 = 499122177;
    int n = a.size();
    for (int i = 1; i < n; i <<= 1)
        for (int j = 0; j < n; j += i << 1)
            for (int k = 0; k < i; k++)
            {
                int x = a[j + k], y = a[i + j + k];
                a[i + j + k] = (1ll * x + y) * inv_2 % mod;
                a[j + k] = (1ll * x - y + mod) % mod * inv_2 % mod;
            }
    return a;
}
std::vector<int> FWT(std::vector<int> a, std::vector<int> b, vector<int> (*f)(vector<int>), vector<int> (*g)(vector<int>))
{
    int n = a.size();
    assert((n & (n - 1)) == 0); // n是2的幂
    a = f(a);
    b = f(b);
    for (int i = 0; i < n; i++)
        a[i] = 1ll * a[i] * b[i] % mod;
    return g(a);
}

3.4 分治NTT（NTT+CQD）

给定序列 $g_{1\dots n - 1}$ ，求序列 $f_{0\dots n - 1}$ 。

其中 $f_i=\sum_{j=1}^if_{i-j}g_j$ ，边界为 $f_0=1$ 。

答案对 $998244353$ 取模。

$2\leq n\leq 10^5$ ， $0\leq g_i<998244353$ 。

利用CDQ分治的思想，先解决左半部分，再解决左半部分对右半部分的贡献。

设当前计算区间为 $[l,r]$ ，此时先 $CDQ$ 已经计算出了 $f[l,\ldots,mid]$ ，考虑其对 $f[mid+1,\ldots,r]$ 的贡献。

对于 $f_k(k\ge mid+1)$ 而言，前半部分所造成的贡献为 $\sum_{i+j=k,i\le mid}f_ig_{k-i}$

也就是说，需要将 $f[l,mid]$ 和 $g(0,r-l)$ 卷积卷起来，对后半部分进行贡献。

所以算出前半部分后，将 $f[l,\ldots,mid]$ 搞成一个多项式，卷积 $NTT$ 计算贡献，加在后面，然后递归后半部分。

复杂度 $O(nlog^2n)$

（本例题也可利用生成函数操纵序列，多项式求逆解决，复杂度 $O(nlogn)$ ）

#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const i64 mod = 998244353;
#define endl '\n'
constexpr int P = 998244353;

int power(int a, int b)
{
    int res = 1;
    for (; b; b /= 2, a = 1LL * a * a % P)
    {
        if (b % 2)
        {
            res = 1LL * res * a % P;
        }
    }
    return res;
}

std::vector<int> rev, roots{0, 1};

void dft(std::vector<int> &a)
{
   //见NTT
}

void idft(std::vector<int> &a)
{
    //见NTT
}

std::vector<int> mul(std::vector<int> a, std::vector<int> b)
{
   //见NTT
}
vector<int> f, g;
void cdq(int l, int r)
{
    if (l == r)
    {
        if (!l)
            f[l] = 1;
        return;
    }
    int mid = (l + r) >> 1;
    cdq(l, mid);
    vector<int> a(mid - l + 1), b(r - l + 1);
    for (int i = l; i <= mid; i++)
        a[i - l] = f[i];
    for (int i = 0; i <= r - l; i++)
        b[i] = g[i];
    a = mul(a, b);
    for (int i = mid + 1; i <= r; i++)
        f[i] = (f[i] + a[i - l]) % P;
    cdq(mid + 1, r);
    return;
}
void solve()
{
    int n;
    cin >> n;
    f.resize(n);
    g.resize(n);
    for (int i = 1; i < n; i++)
    {
        cin >> g[i];
    }
    g[0] = 0;
    cdq(0, n - 1);
    for (int i = 0; i < n; i++)
    {
        cout << f[i] << " ";
    }
}

signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
    // cin >> t;
    while (t--)
        solve();
}

3.5 Poly.h, with NTT&Modint.h

/**   多项式相关（Poly, with. MInt & MLong）
 *    2023-09-20: https://atcoder.jp/contests/arc163/submissions/45737810
 *    2024-07-28: https://codeforces.com/contest/1991/submission/273204889
 **/
#ifndef __POLYS_H__
#define __POLYS_H__
#include <bits/stdc++.h>
#include <icpc-model/Modint.h>
using namespace Modint;
constexpr int P = 998244353;
using Z = MInt<P>;
using i64 = long long;
std::vector<int> rev;
template <int P>
std::vector<MInt<P>> roots{0, 1};

template <int P>
constexpr MInt<P> findPrimitiveRoot()
{
    MInt<P> i = 2;
    int k = __builtin_ctz(P - 1);
    while (true)
    {
        if (power(i, (P - 1) / 2) != 1)
        {
            break;
        }
        i += 1;
    }
    return power(i, (P - 1) >> k);
}

template <int P>
constexpr MInt<P> primitiveRoot = findPrimitiveRoot<P>();

template <>
constexpr MInt<998244353> primitiveRoot<998244353>{31};

template <int P>
constexpr void dft(std::vector<MInt<P>> &a)
{
    int n = a.size();

    if (int(rev.size()) != n)
    {
        int k = __builtin_ctz(n) - 1;
        rev.resize(n);
        for (int i = 0; i < n; i++)
        {
            rev[i] = rev[i >> 1] >> 1 | (i & 1) << k;
        }
    }

    for (int i = 0; i < n; i++)
    {
        if (rev[i] < i)
        {
            std::swap(a[i], a[rev[i]]);
        }
    }
    if (roots<P>.size() < n)
    {
        int k = __builtin_ctz(roots<P>.size());
        roots<P>.resize(n);
        while ((1 << k) < n)
        {
            auto e = power(primitiveRoot<P>, 1 << (__builtin_ctz(P - 1) - k - 1));
            for (int i = 1 << (k - 1); i < (1 << k); i++)
            {
                roots<P>[2 * i] = roots<P>[i];
                roots<P>[2 * i + 1] = roots<P>[i] * e;
            }
            k++;
        }
    }
    for (int k = 1; k < n; k *= 2)
    {
        for (int i = 0; i < n; i += 2 * k)
        {
            for (int j = 0; j < k; j++)
            {
                MInt<P> u = a[i + j];
                MInt<P> v = a[i + j + k] * roots<P>[k + j];
                a[i + j] = u + v;
                a[i + j + k] = u - v;
            }
        }
    }
}

template <int P>
constexpr void idft(std::vector<MInt<P>> &a)
{
    int n = a.size();
    std::reverse(a.begin() + 1, a.end());
    dft(a);
    MInt<P> inv = (1 - P) / n;
    for (int i = 0; i < n; i++)
    {
        a[i] *= inv;
    }
}

template <int P = 998244353>
struct Poly : public std::vector<MInt<P>>
{
    using Value = MInt<P>;

    Poly() : std::vector<Value>() {}
    explicit constexpr Poly(int n) : std::vector<Value>(n) {}

    explicit constexpr Poly(const std::vector<Value> &a) : std::vector<Value>(a) {}
    constexpr Poly(const std::initializer_list<Value> &a) : std::vector<Value>(a) {}

    template <class InputIt, class = std::_RequireInputIter<InputIt>>
    explicit constexpr Poly(InputIt first, InputIt last) : std::vector<Value>(first, last) {}
    /*
    @brief 通过函数生成多项式
    @param n 生成的多项式的长度
    @param f 生成多项式的函数
    */
    template <class F>
    explicit constexpr Poly(int n, F f) : std::vector<Value>(n)
    {
        for (int i = 0; i < n; i++)
        {
            (*this)[i] = f(i);
        }
    }
    /*
    @brief 多项式位移
    @param k 位移的距离，正数表示各项乘以 x^k，负数表示各项除以 x^k
    @return 位移后的多项式
    */
    constexpr Poly shift(int k) const
    {
        if (k >= 0)
        {
            auto b = *this;
            b.insert(b.begin(), k, 0);
            return b;
        }
        else if (this->size() <= -k)
        {
            return Poly();
        }
        else
        {
            return Poly(this->begin() + (-k), this->end());
        }
    }
    // 多项式重塑，将多项式的长度调整为 k
    constexpr Poly trunc(int k) const
    {
        Poly f = *this;
        f.resize(k);
        return f;
    }
    // 多项式加法
    constexpr friend Poly operator+(const Poly &a, const Poly &b)
    {
        Poly res(std::max(a.size(), b.size()));
        for (int i = 0; i < a.size(); i++)
        {
            res[i] += a[i];
        }
        for (int i = 0; i < b.size(); i++)
        {
            res[i] += b[i];
        }
        return res;
    }
    // 多项式减法
    constexpr friend Poly operator-(const Poly &a, const Poly &b)
    {
        Poly res(std::max(a.size(), b.size()));
        for (int i = 0; i < a.size(); i++)
        {
            res[i] += a[i];
        }
        for (int i = 0; i < b.size(); i++)
        {
            res[i] -= b[i];
        }
        return res;
    }
    // 多项式取负
    constexpr friend Poly operator-(const Poly &a)
    {
        std::vector<Value> res(a.size());
        for (int i = 0; i < int(res.size()); i++)
        {
            res[i] = -a[i];
        }
        return Poly(res);
    }
    // 多项式乘法，NTT快速数论变换
    constexpr friend Poly operator*(Poly a, Poly b)
    {
        if (a.size() == 0 || b.size() == 0)
        {
            return Poly();
        }
        if (a.size() < b.size())
        {
            std::swap(a, b);
        }
        int n = 1, tot = a.size() + b.size() - 1;
        while (n < tot)
        {
            n *= 2;
        }
        if (((P - 1) & (n - 1)) != 0 || b.size() < 128)
        {
            Poly c(a.size() + b.size() - 1);
            for (int i = 0; i < a.size(); i++)
            {
                for (int j = 0; j < b.size(); j++)
                {
                    c[i + j] += a[i] * b[j];
                }
            }
            return c;
        }
        a.resize(n);
        b.resize(n);
        dft(a);
        dft(b);
        for (int i = 0; i < n; ++i)
        {
            a[i] *= b[i];
        }
        idft(a);
        a.resize(tot);
        return a;
    }
    constexpr friend Poly operator*(Value a, Poly b)
    {
        for (int i = 0; i < int(b.size()); i++)
        {
            b[i] *= a;
        }
        return b;
    }
    constexpr friend Poly operator*(Poly a, Value b)
    {
        for (int i = 0; i < int(a.size()); i++)
        {
            a[i] *= b;
        }
        return a;
    }
    constexpr friend Poly operator/(Poly a, Value b)
    {
        for (int i = 0; i < int(a.size()); i++)
        {
            a[i] /= b;
        }
        return a;
    }
    constexpr Poly &operator+=(Poly b)
    {
        return (*this) = (*this) + b;
    }
    constexpr Poly &operator-=(Poly b)
    {
        return (*this) = (*this) - b;
    }
    constexpr Poly &operator*=(Poly b)
    {
        return (*this) = (*this) * b;
    }
    constexpr Poly &operator*=(Value b)
    {
        return (*this) = (*this) * b;
    }
    constexpr Poly &operator/=(Value b)
    {
        return (*this) = (*this) / b;
    }
    // 多项式求导
    constexpr Poly deriv() const
    {
        if (this->empty())
        {
            return Poly();
        }
        Poly res(this->size() - 1);
        for (int i = 0; i < this->size() - 1; ++i)
        {
            res[i] = (i + 1) * (*this)[i + 1];
        }
        return res;
    }
    // 多项式积分
    constexpr Poly integr() const
    {
        Poly res(this->size() + 1);
        for (int i = 0; i < this->size(); ++i)
        {
            res[i + 1] = (*this)[i] / (i + 1);
        }
        return res;
    }
    // 多项式求逆，中间m为模多项式长度，即 mod x^m
    constexpr Poly inv(int m) const
    {
        Poly x{(*this)[0].inv()};
        int k = 1;
        while (k < m)
        {
            k *= 2;
            x = (x * (Poly{2} - trunc(k) * x)).trunc(k);
        }
        return x.trunc(m);
    }
    // 多项式求lnx
    constexpr Poly log(int m) const
    {
        return (deriv() * inv(m)).integr().trunc(m);
    }
    // 多项式求e^x
    constexpr Poly exp(int m) const
    {
        Poly x{1};
        int k = 1;
        while (k < m)
        {
            k *= 2;
            x = (x * (Poly{1} - x.log(k) + trunc(k))).trunc(k);
        }
        return x.trunc(m);
    }
    // 多项式快速幂
    constexpr Poly pow(int k, int m) const
    {
        int i = 0;
        while (i < this->size() && (*this)[i] == 0)
        {
            i++;
        }
        if (i == this->size() || 1LL * i * k >= m)
        {
            return Poly(m);
        }
        Value v = (*this)[i];
        auto f = shift(-i) * v.inv();
        return (f.log(m - i * k) * k).exp(m - i * k).shift(i * k) * power(v, k);
    }
    // 多项式开根
    constexpr Poly sqrt(int m) const
    {
        Poly x{1};
        int k = 1;
        while (k < m)
        {
            k *= 2;
            x = (x + (trunc(k) * x.inv(k)).trunc(k)) * CInv<2, P>;
        }
        return x.trunc(m);
    }
    // 多项式转置乘法，计算F(x)*G(1/x)的结果，抹掉负次方项
    constexpr Poly mulT(Poly b) const
    {
        if (b.size() == 0)
        {
            return Poly();
        }
        int n = b.size();
        std::reverse(b.begin(), b.end());
        return ((*this) * b).shift(-(n - 1));
    }
    // 多项式多点求值
    constexpr std::vector<Value> eval(std::vector<Value> x) const
    {
        if (this->size() == 0)
        {
            return std::vector<Value>(x.size(), 0);
        }
        const int n = std::max(x.size(), this->size());
        std::vector<Poly> q(4 * n);
        std::vector<Value> ans(x.size());
        x.resize(n);
        std::function<void(int, int, int)> build = [&](int p, int l, int r)
        {
            if (r - l == 1)
            {
                q[p] = Poly{1, -x[l]};
            }
            else
            {
                int m = (l + r) / 2;
                build(2 * p, l, m);
                build(2 * p + 1, m, r);
                q[p] = q[2 * p] * q[2 * p + 1];
            }
        };
        build(1, 0, n);
        std::function<void(int, int, int, const Poly &)> work = [&](int p, int l, int r, const Poly &num)
        {
            if (r - l == 1)
            {
                if (l < int(ans.size()))
                {
                    ans[l] = num[0];
                }
            }
            else
            {
                int m = (l + r) / 2;
                work(2 * p, l, m, num.mulT(q[2 * p + 1]).trunc(m - l));
                work(2 * p + 1, m, r, num.mulT(q[2 * p]).trunc(r - m));
            }
        };
        work(1, 0, n, mulT(q[1].inv(n)));
        return ans;
    }
};

template <int P = 998244353>
Poly<P> berlekampMassey(const Poly<P> &s)
{
    Poly<P> c;
    Poly<P> oldC;
    int f = -1;
    for (int i = 0; i < s.size(); i++)
    {
        auto delta = s[i];
        for (int j = 1; j <= c.size(); j++)
        {
            delta -= c[j - 1] * s[i - j];
        }
        if (delta == 0)
        {
            continue;
        }
        if (f == -1)
        {
            c.resize(i + 1);
            f = i;
        }
        else
        {
            auto d = oldC;
            d *= -1;
            d.insert(d.begin(), 1);
            MInt<P> df1 = 0;
            for (int j = 1; j <= d.size(); j++)
            {
                df1 += d[j - 1] * s[f + 1 - j];
            }
            assert(df1 != 0);
            auto coef = delta / df1;
            d *= coef;
            Poly<P> zeros(i - f - 1);
            zeros.insert(zeros.end(), d.begin(), d.end());
            d = zeros;
            auto temp = c;
            c += d;
            if (i - temp.size() > f - oldC.size())
            {
                oldC = temp;
                f = i;
            }
        }
    }
    c *= -1;
    c.insert(c.begin(), 1);
    return c;
}

template <int P = 998244353>
MInt<P> linearRecurrence(Poly<P> p, Poly<P> q, i64 n)
{
    int m = q.size() - 1;
    while (n > 0)
    {
        auto newq = q;
        for (int i = 1; i <= m; i += 2)
        {
            newq[i] *= -1;
        }
        auto newp = p * newq;
        newq = q * newq;
        for (int i = 0; i < m; i++)
        {
            p[i] = newp[i * 2 + n % 2];
        }
        for (int i = 0; i <= m; i++)
        {
            q[i] = newq[i * 2];
        }
        n /= 2;
    }
    return p[0] / q[0];
}

struct Comb
{
    int n;
    std::vector<Z> _fac;
    std::vector<Z> _invfac;
    std::vector<Z> _inv;

    Comb() : n{0}, _fac{1}, _invfac{1}, _inv{0} {}
    Comb(int n) : Comb()
    {
        init(n);
    }

    void init(int m)
    {
        m = std::min(m, Z::getMod() - 1);
        if (m <= n)
            return;
        _fac.resize(m + 1);
        _invfac.resize(m + 1);
        _inv.resize(m + 1);

        for (int i = n + 1; i <= m; i++)
        {
            _fac[i] = _fac[i - 1] * i;
        }
        _invfac[m] = _fac[m].inv();
        for (int i = m; i > n; i--)
        {
            _invfac[i - 1] = _invfac[i] * i;
            _inv[i] = _invfac[i] * _fac[i - 1];
        }
        n = m;
    }

    Z fac(int m)
    {
        if (m > n)
            init(2 * m);
        return _fac[m];
    }
    Z invfac(int m)
    {
        if (m > n)
            init(2 * m);
        return _invfac[m];
    }
    Z inv(int m)
    {
        if (m > n)
            init(2 * m);
        return _inv[m];
    }
    Z binom(int n, int m)
    {
        if (n < m || m < 0)
            return 0;
        return fac(n) * invfac(m) * invfac(n - m);
    }
} comb;

Poly<P> get(int n, int m)
{
    if (m == 0)
    {
        return Poly(n + 1);
    }
    if (m % 2 == 1)
    {
        auto f = get(n, m - 1);
        Z p = 1;
        for (int i = 0; i <= n; i++)
        {
            f[n - i] += comb.binom(n, i) * p;
            p *= m;
        }
        return f;
    }
    auto f = get(n, m / 2);
    auto fm = f;
    for (int i = 0; i <= n; i++)
    {
        fm[i] *= comb.fac(i);
    }
    Poly pw(n + 1);
    pw[0] = 1;
    for (int i = 1; i <= n; i++)
    {
        pw[i] = pw[i - 1] * (m / 2);
    }
    for (int i = 0; i <= n; i++)
    {
        pw[i] *= comb.invfac(i);
    }
    fm = fm.mulT(pw);
    for (int i = 0; i <= n; i++)
    {
        fm[i] *= comb.invfac(i);
    }
    return f + fm;
}
#endif

3.6 多项式求逆

给定一个多项式 $F(x)$ ，请求出一个多项式 $G(x)$ ，满足 $F(x) * G(x) \equiv 1 \pmod{x^n}$ 。系数对 $998244353$ 取模。

对于 $100\%$ 的数据， $1 \leq n \leq 10^5$ ，$ 0 \leq a_i \leq 10^9$。

工作原理：

我们不妨假设， $n=2^k$ , $k\in N$ 。

若 $n=1$ ，则 $A(x)×B(x)≡a_0×b_0≡1(mod\ x^1)$ ,其中 $a_0$ ， $b_0$ 表示多项式 $A$ 和多项式 $B$ 的常数项。

若需要求出 $b_0$ ，直接用费马小定理求出 $a_0$ 的乘法逆元即可。

当 $n>1$ 时：

我们假设在模 $x^{\frac{n}{2}}$ 的意义下 $A(x)$ 的逆元 $B^′(x)$ 我们已经求得。

依据定义，则有

$A(x)B^′(x)≡1(mod\ x^{\frac{n}{2}})$ (1)

对(1)式进行移项得

$A(x)B^′(x)−1≡0(mod\ x^{\frac{n}{2}})$ (2)

然后对(2)式等号两边平方，得

$A^2(x)B^{′2}(x)−2A(x)B^′(x)+1≡0(mod\ x^n)$ (3)

将常数项移动到等式右侧，得

$A^2(x)B^{′2}(x)−2A(x)B^′(x)≡−1(mod\ x^n)$ (4)

将等式两边去相反数，得

$2A(x)B^′(x)−A^2(x)B^{′2}(x)≡1(mod\ x^n)$ (5)

下面考虑回我们需要求的多项式 $B(x)$ ，依据定义，其满足

$A(x)B(x)≡1(mod\ x^n)$ (6)

将(5)−(6)并移项，得

$A(x)B(x)≡2A(x)B^′(x)−A^2(x)B^{′2}(x)(mod\ x^n)$ (7)

等式两边约去 $A(x)$ ，得

$B(x)≡2B′(x)−A(x)B^{′2}(x)(mod\ x^n)$ (8)

void solve()
{
    int n;
    cin >> n;
    vector<Z> a(n);
    for (auto &i : a)
        cin >> i;
    Poly<P> A(a);
    Poly<P> invA = A.inv(n);
    for (auto &i : invA)
    {
        cout << i << " ";
    }
    cout << endl;
}

3.7 多项式除法

严格注意：多项式除法不可以拿来做高精度除法！因为多项式除法做了取余数的操作！相当于扣了项的系数！

给定一个 $n$ 次多项式 $F(x)$ 和一个 $m$ 次多项式 $G(x)$ ，请求出多项式 $Q(x)$ , $R(x)$ ，满足以下条件：

$Q(x)$ 次数为 $n-m$ ， $R(x)$ 次数小于 $m$
$F(x) = Q(x) G(x) + R(x)$

所有的运算在模 $998244353$ 意义下进行。

如果 $R(x)$ 不足 $m-1$ 次，多余的项系数补 $0$ 。

对于所有数据， $1 \le m < n \le 10^5$ ，给出的系数均属于 $[0, 998244353) \cap \mathbb{Z}$ 。

$N$ 次多项式 $A(x)$ 的系数 $vector$ 进行一次 $reverse$ 后表示的是 $A(\frac{1}{x})x^N$ 的系数。

故求多项式除法 $A(x)=B(x)C(x)+D(x)$ 时，考虑 $x^NA(\frac{1}{x})=x^MB(\frac{1}{x})x^{N-M}C(\frac{1}{x})+D(\frac{1}{x})$

多项式对 $x^{N-M+1}$ 求模， $D(x)$ 消失，有 $x^{N-M}C(\frac{1}{x})\equiv \frac{A^{'}(x)}{B^{'}(x)}$

void solve()
{
    int n, k;
    cin >> n >> k;
    vector<Z> a(n + 1), b(k + 1);
    for (auto &i : a)
        cin >> i;
    for (auto &i : b)
        cin >> i;
    Poly<P> A(a), B(b);
    reverse(A.begin(), A.end());
    reverse(B.begin(), B.end());
    A.resize(n - k + 1);
    B.resize(n - k + 1);
    Poly<P> C = A * (B.inv(n - k + 1));
    C.resize(n - k + 1);
    reverse(C.begin(), C.end());
    for (auto &i : C)
        cout << i << " ";
    cout << endl;
    Poly<P> D = Poly<P>(a) - Poly<P>(b) * C;
    D.resize(k);
    for (auto &i : D)
        cout << i << " ";
}

3.8 多项式对数

求个导再积分就行。

给定多项式 $A(x)$ ，求 $B(x)$ 使得 $B(x)\equiv lnA(x)\ (mod\ x^n)$ ，保证 $a_0=1$

void solve()
{
    int n;
    cin >> n;
    vector<Z> a(n);
    for (auto &x : a)
        cin >> x;
    Poly<P> p(a);
    auto b = p.log(n);
    for (auto x : b)
        cout << x << ' ';
    cout << endl;
}

3.9 多项式自然指数

给定多项式 $A(x)$ ，求 $B(x)$ 使得 $B(x)\equiv e^{A(x)}\ (mod\ x^n)$ ，保证 $a_0=0$

函数求导，牛顿迭代法。

先从牛顿迭代讲起。

已知多项式函数 $G(z)$ ，求多项式函数 $F(x)$ 满足 $$G(F(x))\equiv0 \pmod{x^n}$$

考虑用迭代求解，假设我们已经求得 $F_0(x)$ 满足 $$G(F_0(x))\equiv0\pmod{x^{\left\lceil\frac{n}{2}\right\rceil}}$$

将函数 $G$ 在 $z=F_0(x)$ 处进行泰勒展开 $$G(F(x))=\sum_{i=1}^{\infty}\frac{G^i(F_0(x))}{i!}(F(x)-F_0(x))^i$$ ,其中 $G^i$ 为 $G$ 的 $i$ 阶导函数.

取前两项 $$G(F(x))\equiv G(F_0(x))+G’(F_0(x))(F(x)-F_0(x))\pmod{x^n}$$

考虑到 $G(F(x))\equiv 0\pmod{x^n}$ $$F(x)\equiv F_0(x)-\frac{G(F_0(x))}{G’(F_0(x))}\pmod{x^n}$$

边界条件即 $f[0]=e^{a_0}$ ，向上迭代即可.

回到本题，考虑到 $$B(x)\equiv e^{A(x)}\pmod{x^n}$$

即 $$\ln B(x)-A(x)\equiv0\pmod{x^n}$$

于是令 $$G(B(x))\equiv\ln B(x)-A(x)\pmod{x^n}$$

由于 $A(x)$ 为常数， $$G’(B(x))=B^{-1}(x)$$ ，套牛顿迭代 $$B(x)\equiv B_0(x)(1-\ln B_0(x)+A(x))\pmod{x^n}$$

void solve()
{
    int n;
    cin >> n;
    vector<Z> a(n);
    for (auto &x : a)
        cin >> x;
    Poly<P> p(a);
    auto b = p.exp(n);
    for (auto x : b)
        cout << x << ' ';
    cout << endl;
}

3.10 多项式多点求值

原理不会，抄就行。

给定一个 $n$ 次多项式 $f(x)$ ，现在请你对于 $i \in [1,m]$ ，求出 $f(a_i)$ 。注意是 $n$ 次，意味着有 $n+1$ 项。

$n,m \in [1,64000]$ ， $a_i,[x^i]f(x) \in [0,998244352]$ 。

$[x^i]f(x)$ 表示 $f(x)$ 的 $i$ 次项系数。

void solve()
{
    int n, m;
    cin >> n >> m;
    Poly<P> f(n + 1);
    for (auto &v : f)
    {
        cin >> v;
    }
    vector<Z> x(m);
    for (auto &v : x)
    {
        cin >> v;
    }
    auto fx = f.eval(x);
    for (auto v : fx)
    {
        cout << v << endl;
    }
}

3.11 多项式快速插值/拉格朗日快速插值

以下默认 $mid=\lfloor\frac{l+r}{2}\rfloor$

由拉格朗日差值公式 $\large F(x)=\sum_{i=1}^n y_i\prod_{j\neq i}\frac{x-x_j}{x_i-x_j}$ 化简得到

$\large F(x)=\sum_{i=1}^n \frac{y_i}{\prod_{j\neq i}(x_i-x_j)}\prod_{j\neq i}(x-x_j)$

设 $\large \delta(x)=\prod_{i=1}^n(x-x_i)$ ，则显然有洛必达法则下， $\large \prod_{j\neq i}(x_i-x_j)=\lim_{x\to x_i}\frac{\delta(x)}{x-x_i}=\delta'(x_i)$

对 $\delta(x)$ 分治 $NTT$ （类似快速幂那种就行了），求导后多点求值得到 $\delta'(x_i)$ .

接下来继续正宗分治 $NTT$ 即可，设 $G_{l,r}(x)=\prod_{i=l}^r(x-x_i)$ ， $H_{l,r}$ 为 $(x_l,y_l),\cdots,(x_r,y_r)$ 插出来的多项式，即 $\sum_{i=l}^r \frac{y_i}{\delta'(x_i)}\prod_{j\neq i,l\le j\le r}(x-x_j)$ ，则有

$G_{l,r}=G_{l,mid}\ \cdot\ G_{mid+1,r}\\ H_{l,r}=H_{l,mid}\ \cdot G_{mid+1,r}\ +\ H_{mid+1,r}\ \cdot\ G_{l,mid}$

分治 $NTT$ 即可。复杂度 $O(nlog^2n)$

3.12 二维卷积

$\large s_{i,j}=\sum_{x_1\circ x_2=i,y_1*y_2=j}a_{x_1,y_1}\times b_{x_2,y_2}$

分5步：

1.对 $a$ 和 $b$ 的每一行做普通 $DFT$ 或对应 $FWT$

2.对 $a$ 和 $b$ 的每一列做普通 $DFT/FWT$

3.新建矩阵 $s$ ， $s_{i,j}=a_{i,j}b_{i,j}$

4.对 $s$ 的每一列做普通 $IDFT/IFWT$ (别忘了做完之后乘上每列长度的逆元)

5.对 $s$ 的每一行做普通 $IDFT/IFWT$ (别忘了做完之后乘上每行长度的逆元)

然后 $s$ 就是要求的结果了。

3.13 普通生成函数操作

普通生成函数操作组合数学计数问题。

举一个例子：

一个长度为 $n$ 的数列，从中取出 $s$ 个数，要求异或结果为 $k$ 的方案数。

操纵生成函数：

$F(x,y)=\prod_{i=1}^n(1+x^{a_i}y)$

这里 $x$ 为异或卷积， $y$ 为正卷积。

则答案为 $[x^{k}y^s]F(x,y)$ ，即对应项系数。一般不会有二维的情况，二维显然无法确定单位根，一般是需要暴力卷积的。本生成函数原题 $ABC367G$ 中 $y$ 是一个长度不超过 $100$ 的循环卷积，问题只在快速沃尔什变换上。

考虑对 $1+x^{a_i}y$ 进行快速沃尔什点值变换，记变换后的点值序列为 $FWT(x^{a_i})=\{g_{a_i}^{w}\}$ ，则由于将 $y$ 于此维度视作常数，由于沃尔什变换线性性有 $FWT(1+x^{a_i}y)=\{1+g_{a_i}^{w}y\}$ .

由于沃尔什变换特性，幂次函数 $x^n$ 的沃尔什变换序列只有 $1$ 和 $-1$ 两种情况，所以沃尔什序列对应位置点值相乘后有 $FWT(F(x,y))_w=[y^0]\prod_{i=1}^n(1+y)^{c_w}(1-y)^{n-c_w}$ ，其中 $c_w$ 为 $FWT(x_{a_i})_w$ 为 $1$ 的 $i$ 的数量。关于 $c_w$ 显然有 $c_w+(n-c_w)\times(-1)=\sum_{i=1}^nh_{a_i}^w$ ，等式右边可以由 $\sum_{i=1}^nx^{a_i}$ 快速沃尔什变换得到（ $FWT$ 线性性）

由于 $y$ 维度很小，暴力卷积卷出来，最后快速沃尔什逆变换后就是结果多项式，直接锁结果就行了。

vector<int> f, a, b, finalans;
vector<vector<int>> presum, presum2;
void solve()
{
    int n, m, k;
    cin >> n >> m >> k;
    f.assign(1 << 20, 0);
    for (int i = 1; i <= n; i++)
    {
        int x;
        cin >> x;
        f[x]++;
    }
    a = fwt_xor(f);
    for (int i = 0; i < (1 << 20); i++)
    {
        a[i] = ((n + a[i]) % mod * (499122177)) % mod;
    }
    // 暴力预处理循环卷积(1+y)^a 以及(1-y)^a
    presum.assign(n + 1, vector<int>(m + 1)), presum2 = presum;
    presum[0][0] = presum2[0][0] = 1;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            presum[i][j] = (presum[i][j] + presum[i - 1][j]) % mod;                              //(1+y)
            presum[i][(j + 1) % m] = (presum[i][(j + 1) % m] + presum[i - 1][j]) % mod;          //(1+y)
            presum2[i][j] = (presum2[i][j] + presum2[i - 1][j]) % mod;                           //(1-y)
            presum2[i][(j + 1) % m] = (presum2[i][(j + 1) % m] - presum2[i - 1][j] + mod) % mod; //(1-y)
        }
    }
    finalans.assign(1 << 20, 0);
    for (int i = 0; i < (1 << 20); i++) // 快速沃尔什变换第i位的值
    {                                   //(1+y)^(a[i])*(1-y)^(n-a[i])
                                        // 求y^0，即y^m项
        for (int j = 0; j < m; j++)
        {
            finalans[i] = (finalans[i] + (presum[a[i]][j] * presum2[n - a[i]][(m - j) % m] % mod)) % mod;
        }
    }
    b = ifwt_xor(finalans);
    i64 ans = 0;
    for (int i = 0; i < (1 << 20); i++)
    {
        ans = (ans + b[i] * power(i, k) % mod) % mod;
    }
    cout << ans << endl;
}

其他见 $OI-Wiki$

3.14 指数生成函数操作

操纵排列数学计数问题。

4. 计算几何相关

4.1 平面几何（with Complex)

/**   平面几何（with. complex）
 *    2023-09-04: https://qoj.ac/submission/164445
**/
using Point = std::complex<long double>;

#define x real
#define y imag

long double dot(const Point &a, const Point &b) {
    return (std::conj(a) * b).x();
}

long double cross(const Point &a, const Point &b) {
    return (std::conj(a) * b).y();
}

long double length(const Point &a) {
    return std::sqrt(dot(a, a));
}

long double dist(const Point &a, const Point &b) {
    return length(a - b);
}

long double get(const Point &a, const Point &b, const Point &c, const Point &d) {
    auto e = a + (b - a) * cross(c - a, d - a) / cross(b - a, d - c);
    return dist(d, e);
}

4.2 二维凸包+旋转卡壳（凸包直径）

#include <bits/stdc++.h>
using namespace std;
// #define DEBUG 1
#define i64 long long
#define d32 double
const int INF = 0x3f3f3f3f;
const int N = 2e6 + 9;
struct node
{
    i64 x, y;
    bool operator<(const node &a) const
    {
        return x == a.x ? y < a.y : x < a.x;
    }
    bool operator==(const node &a) const
    {
        return x == a.x && y == a.y;
    }
    node operator-(const node &a) const
    {
        return {x - a.x, y - a.y};
    }
    i64 operator*(const node &a) const
    {
        return x * a.y - y * a.x;
    }
    i64 operator^(const node &a) const
    {
        return x * a.x + y * a.y;
    }
    node operator+(const node &a) const
    {
        return {x + a.x, y + a.y};
    }
    friend d32 dis(node a, node b)
    {
        return sqrtl((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
    }
    friend i64 dis2(node a, node b)
    {
        return (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y);
    }
};
int stk[N], tp = 0;
bool used[N];

//返回的vector0位空出，最后一位为第一个点
vector<node> get_convex(node p[], int n)
{
    // stk[] 是整型，存的是下标
    // p[] 存储向量或点
    // h[] 存储凸包上的点
    // used[] 标记是否在凸包上
    // tp 栈顶指针
    tp = 0; // 初始化栈
            // 标记是否在凸包上
    for (int i = 1; i <= n; i++)
    {
        used[i] = 0;
    }
    std::sort(p + 1, p + 1 + n); // 对点进行排序
    stk[++tp] = 1;
    // 栈内添加第一个元素，且不更新 used，使得 1 在最后封闭凸包时也对单调栈更新
    for (int i = 2; i <= n; ++i)
    {
        while (tp >= 2 // 下一行 * 操作符被重载为叉积
               && (p[stk[tp]] - p[stk[tp - 1]]) * (p[i] - p[stk[tp]]) <= 0)
            used[stk[tp--]] = 0;
        used[i] = 1; // used 表示在凸壳上
        stk[++tp] = i;
    }
    int tmp = tp; // tmp 表示下凸壳大小
    for (int i = n - 1; i > 0; --i)
        if (!used[i])
        {
            // ↓求上凸壳时不影响下凸壳
            while (tp > tmp && (p[stk[tp]] - p[stk[tp - 1]]) * (p[i] - p[stk[tp]]) <= 0)
                used[stk[tp--]] = 0;
            used[i] = 1;
            stk[++tp] = i;
        }
    vector<node> h;
    h.push_back({-INF, -INF});    // 从 1 开始存储凸包上的点
    for (int i = 1; i <= tp; ++i) // 复制到新数组中去
        h.push_back(p[stk[i]]);
    int ans = tp - 1;
    return h;
}
bool is[N];
// 求凸包直径，返回直径的平方
i64 get_longest(vector<node> sta)
{
#ifdef DEBUG
    cout << "-------------------DEBUG-------------------" << endl;
    cout << "points in convex hull:" << endl;
    for (auto i : sta)
    {
        cout << i.x << " " << i.y << endl;
    }
    cout << "-------------------DEBUG-------------------" << endl;
#endif
    i64 mx = 0;               // 求凸包直径
    int top = sta.size() - 1; // 将凸包上的节点编号存在栈里，第一个和最后一个节点编号相同
    int j = 3;
    if (top < 4)
    {
        mx = dis2(sta[1], sta[2]);
        return mx;
    }
    for (int i = 1; i < top; i++)
    {
        while ((sta[i + 1] - sta[i]) * (sta[j] - sta[i + 1]) <= (sta[i + 1] - sta[i]) * (sta[j % top + 1] - sta[i + 1]))
        {
#ifdef DEBUG
            cout << "-------------------DEBUG-------------------" << endl;
            cout << "i=" << i << " j=" << j << endl;
            cout << "sta[i]=" << sta[i].x << " " << sta[i].y << endl;
            cout << "sta[i+1]=" << sta[i + 1].x << " " << sta[i + 1].y << endl;
            cout << "sta[j]=" << sta[j].x << " " << sta[j].y << endl;
            cout << "sta[j%top+1]=" << sta[j % top + 1].x << " " << sta[j % top + 1].y << endl;
            cout << "-------------------DEBUG-------------------" << endl;
#endif
            j = j % top + 1;
        }
#ifdef DEBUG
        cout << "-------------------DEBUG-------------------" << endl;
        cout << "mx=" << mx << endl;
        cout << "dis2(sta[" << i << "],sta[" << j << "])=" << dis2(sta[i], sta[j]) << endl;
        cout << "dis2(sta[" << i + 1 << "],sta[" << j << "])=" << dis2(sta[i + 1], sta[j]) << endl;
        cout << "-------------------DEBUG-------------------" << endl;
#endif
        mx = max(mx, max(dis2(sta[i], sta[j]), dis2(sta[i + 1], sta[j])));
    }
    return mx;
}
node a[N + 1], b[N + 1];
void solve()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i].x >> a[i].y;
    }
    vector<node> h = get_convex(a, n);
    int cnt = h.size() - 2;
    d32 C = 0;
    for (int i = 1; i <= cnt; i++)
    {
        C += dis(h[i], h[i + 1]);
    }

    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> b[i].x >> b[i].y;
    }
    h.clear();
    h = get_convex(b, n);
    d32 D = sqrtl(get_longest(h));
    // cout << C << endl;
    cout << fixed << setprecision(10) << C + 2 * M_PI * D << endl;
    return;
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

5. 组合数学相关

5.1 组合数杨辉三角+线性递推逆元

#include<iostream>

using namespace std;
int n,m;
int f[1005][1005];

int main()
{
    cin>>n>>m;
    for(int i=0;i<=n;i++)
    {
        f[i][i]=1;
        f[i][0]=1;
    }
    for(int i=1;i<=n;i++)
        for(int j=1;j<i;j++)
            f[i][j]=f[i-1][j]+f[i-1][j-1];
    cout<<f[n][m];
    return 0;
}

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
int mod;
const int maxn = 6e6 + 9;
int inv[maxn];
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int a;
    cin >> a >> mod;
    inv[1] = 1;
    cout << 1 << endl;
    for (int i = 2; i <= a; i++)
    {
        inv[i] = (mod - mod / i) * inv[mod % i] % mod;
        cout << inv[i] << endl;
    }
}

5.2 卢卡斯定理/扩展卢卡斯定理

$C_n^{m}\ mod\ p=C_{\lfloor \frac{n}{p}\rfloor}^{\lfloor \frac{m}{p}\rfloor}\cdot C_{n\ mod\ p}^{m\ mod\ p}\ mod \ p$

强制要求 $p$ 为质数。复杂度 $O(p+Tlogn)$

long long C(long long n,long long m,long long mod)
{
    if(m>n&&n==0)return 0;
    if(m==0)return 1;
    return ((frac[n]*invq[m]%mod)*invq[n-m])%mod;
}
//阶乘的值和逆元预处理是线性的递推
long long Lucas(long long n, long long m, long long p)
{
    if (m == 0)
        return 1;
    return (C(n % p, m % p, p) * Lucas(n / p, m / p, p)) % p;
}

对于扩展卢卡斯定理，不再要求 $p$ 必须是质数，原理见 $OI-Wiki$ 。注意，单次询问 $O(plogp)$ 复杂度，基本不可能支持大量次数询问。模板也是仅支持查询一次的。

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <iostream>
#include <climits>
#include <cmath>
using namespace std;
namespace ExLucas
{
    const int N = 1e6;
    typedef long long ll;
    ll n, m, p;
    inline ll power(ll a, ll b, const ll p = LLONG_MAX)
    {
        ll ans = 1;
        while (b)
        {
            if (b & 1)
                ans = ans * a % p;
            a = a * a % p;
            b >>= 1;
        }
        return ans;
    }
    ll fac(const ll n, const ll p, const ll pk)
    {
        if (!n)
            return 1;
        ll ans = 1;
        for (int i = 1; i < pk; i++)
            if (i % p)
                ans = ans * i % pk;
        ans = power(ans, n / pk, pk);
        for (int i = 1; i <= n % pk; i++)
            if (i % p)
                ans = ans * i % pk;
        return ans * fac(n / p, p, pk) % pk;
    }
    ll exgcd(const ll a, const ll b, ll &x, ll &y)
    {
        if (!b)
        {
            x = 1, y = 0;
            return a;
        }
        ll xx, yy, g = exgcd(b, a % b, xx, yy);
        x = yy;
        y = xx - a / b * yy;
        return g;
    }
    ll inv(const ll a, const ll p)
    {
        ll x, y;
        exgcd(a, p, x, y);
        return (x % p + p) % p;
    }
    ll C(const ll n, const ll m, const ll p, const ll pk)
    {
        if (n < m)
            return 0;
        ll f1 = fac(n, p, pk), f2 = fac(m, p, pk), f3 = fac(n - m, p, pk), cnt = 0;
        for (ll i = n; i; i /= p)
            cnt += i / p;
        for (ll i = m; i; i /= p)
            cnt -= i / p;
        for (ll i = n - m; i; i /= p)
            cnt -= i / p;
        return f1 * inv(f2, pk) % pk * inv(f3, pk) % pk * power(p, cnt, pk) % pk;
    }
    ll a[N], c[N];
    int cnt;
    inline ll CRT()
    {
        ll M = 1, ans = 0;
        for (int i = 0; i < cnt; i++)
            M *= c[i];
        for (int i = 0; i < cnt; i++)
            ans = (ans + a[i] * (M / c[i]) % M * inv(M / c[i], c[i]) % M) % M;
        return ans;
    }
    ll exlucas(const ll n, const ll m, ll p)
    {
        ll tmp = sqrt(p);
        for (int i = 2; p > 1 && i <= tmp; i++)
        {
            ll tmp = 1;
            while (p % i == 0)
                p /= i, tmp *= i;
            if (tmp > 1)
                a[cnt] = C(n, m, i, tmp), c[cnt++] = tmp;
        }
        if (p > 1)
            a[cnt] = C(n, m, p, p), c[cnt++] = p;
        return CRT();
    }
    int work()
    {
        ios::sync_with_stdio(false);
        cin >> n >> m >> p;
        cout << exlucas(n, m, p);
        return 0;
    }
}
int main()
{
    return zyt::work();
}

5.3 $Catlan$ 数与 $Fibonacci$ 数列

$H_n=\frac{2n!}{n+1},n\ge 2$ ，维护一种绝对大于等于的关系，比如固定入栈顺序，有多少种出栈顺序（保证栈内元素数量一定大于等于总出栈元素数量）

数列皮亚诺周期不超过 $6k$ ， $k$ 为模数。强行解周期可以考虑矩阵原根计算，因为矩阵 $mod$ $p$ 最小周期是皮亚诺周期，所以根号开 $\sqrt {6k+1}$ .

#include <bits/stdc++.h>
#define umap unordered_map
using namespace std;
typedef long long ll;
typedef unsigned long long ull;

string S;
ll MOD;

const int L = 2;
const ull BASE = 13331;
struct Matrix {
    ll M[L+1][L+1];
    ll *operator[](int p) {
        return M[p];
    }
    void clear() {
        memset(M, 0, sizeof M);
    }
    void reset() {
        clear();
        for (int i = 1; i <= L; i++)
            M[i][i] = 1;
    }
    Matrix friend operator*(Matrix A, Matrix B) {
        Matrix C; C.clear();
        for (int i = 1; i <= L; i++)
            for (int k = 1; k <= L; k++)
                for (int j = 1; j <= L; j++)
                    (C[i][j] += A[i][k] * B[k][j] % MOD) %= MOD;
        return C;
    }
    ull hs() { // hash
        ull ret = 0;
        for (int i = 1; i <= L; i++)
            for (int j = 1; j <= L; j++)
                ret = ret * BASE + M[i][j];
        return ret;
    }

};
Matrix qpow(Matrix A, ll b) {
    Matrix Ret; Ret.reset();
    while (b) {
        if (b & 1)
            Ret = Ret * A;
        A = A * A;
        b >>= 1;
    }
    return Ret;
}

ll BSGS(Matrix A, Matrix B) {
    umap<ull, ll> mp;
    ll t = sqrt(MOD * 6) + 1;
    Matrix Cur; Cur.reset();
    for (ll i = 1; i <= t; i++) {
        mp[(Cur * B).hs()] = i-1;
        Cur = A * Cur;
    }
    Matrix Cur2 = Cur;
    for (ll i = 1; i <= t; i++) {
        if (mp.find(Cur2.hs()) != mp.end())
            return i * t - mp[Cur2.hs()];
        Cur2 = Cur * Cur2;
    }
    return -1;
}

Matrix A, I;
void init() {
    A[1][1] = 1; A[1][2] = 1;
    A[2][1] = 1; A[2][2] = 0;

    I[1][1] = 1; I[1][2] = 0;
    I[2][1] = 0; I[2][2] = 1;
}

ll fib(ll n) {
    if (n == 0)
        return 0;
    return qpow(A, n-1)[1][1];
}

int main() { ios::sync_with_stdio(0); cin.tie(0);
    cin >> S >> MOD;
    if (MOD == 1) {
        cout << 0 << endl;
        return 0;
    }
    init();
    ll pi = BSGS(A, I);
    ll n = 0;
    for (auto c : S)
        n = (n * 10 + (c - '0')) % pi;
    cout << fib(n) << endl;
    return 0;
}

查 $OI-Wiki$

6. 位运算相关技巧杂谈

异或是特殊的矩阵加法，在 $<Z_2^n,xor,and>$ 下。
连续从 $1$ 到 $n$ 的异或和是有规律的，对于模 $4$ 剩余下有余 $1$ 得 $1$ ，余 $2$ 得 $n+1$ ，余 $3$ 得 $0$ ，余 $0$ 得 $n$ .
区间异或和可表示两个前缀异或的异或和。
带递归形式的 $f(x)=f(\frac{x}{3})$ 等之类的关注位运算进制表示规律。
$a+b=2(a\&b)+(a\oplus b)$

Part 3. 杂项技巧

3.1 普通莫队

假设 $n=m$ ,那么对于序列上的区间询问问题,如果从 $[l,r]$ 的答案能够 $O(1)$ 扩展到 $[l-1,r],[l+1,r],[l,r+1],[l,r-1]$ （即与 $[l,r]$ 相邻的区间）的答案,那么可以在 $O(n\sqrt n)$ 的复杂度内求出所有询问的答案。

莫队需要相当牛逼的卡常，基本上禁用一切 $mapSTL$ ，实在必要需要手搓哈希表。

#include <bits/stdc++.h>
using namespace std;
#define i64 long long
int block; // 莫队分块大小
struct node
{
    int l, r, id;
    bool operator<(const node &x) const
    {
        if (l / block != x.l / block)
            return l < x.l;
        // 注意下面两行不能写小于（大于）等于，否则会出错（详见下面的小细节）
        if ((l / block) & 1)
            return r < x.r;
        return r > x.r;
    }
};
int sum = 0;
const int maxn = 2e5 + 9;
const int inf = 1e6 + 9;
int mp[inf];
int a[maxn];
void add(int pos)
{
    if (mp[a[pos]])
        sum--;
    else
        sum++;
    mp[a[pos]] ^= 1;
}
void del(int pos)
{
    if (mp[a[pos]])
        sum--;
    else
        sum++;
    mp[a[pos]] ^= 1;
}
int n;
void solve()
{
    sum = 0;
    int n, q;
    cin >> n >> q;
    block = sqrt(n);
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        mp[a[i]] = 0;
    }
    vector<node> qs;
    for (int i = 0; i < q; i++)
    {
        int l, r;
        cin >> l >> r;
        qs.push_back({l, r, i});
    }
    vector<int> ans(q);
    sort(qs.begin(), qs.end());
    int l = 1, r = 0;
    for (int i = 0; i < q; i++)//莫队算法灵魂
    {
        while (l > qs[i].l)
            add(--l);
        while (r < qs[i].r)
            add(++r);
        while (l < qs[i].l)
            del(l++);
        while (r > qs[i].r)
            del(r--);
        ans[qs[i].id] = sum;
    }
    for (int i = 0; i < q; i++)
    {
        if (ans[i])
        {
            cout << "NO" << endl;
        }
        else
            cout << "YES" << endl;
    }
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t;
    cin >> t;
    while (t--)
        solve();
    return 0;
}

3.2 带修改莫队

普通莫队算法不支持修改，需要带修改的莫队。带修改莫队唯一的区别就是加上了一个时间戳维度，变成了多维莫队。

然后跳时间戳就行了，改少了就多改，改多了就改回去。

注意，带修改莫队常数较大，分块 $n^{\frac{2}{3}}$ ，时间复杂度 $O(n^{\frac{5}{3}})$ ，不要带奇偶排序

#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const i64 mod = 998244353;
#define endl '\n'
int block;
struct qnode
{
    int l, r, id, t;
    bool operator<(const qnode &x) const
    {
        if (l / block != x.l / block)
            return l < x.l;
        if (r / block != x.r / block)
            return r < x.r;
        return t < x.t;
    };
};
vector<array<int, 2>> upd(1);
vector<int> mp(1e7);
int sum = 0;
void add(int x)
{
    mp[x]++;
    if (mp[x] == 1)
        sum++;
}
void del(int x)
{
    mp[x]--;
    if (mp[x] == 0)
        sum--;
}
void solve()
{
    int n, q;
    cin >> n >> q;
    vector<int> a(n);
    for (int i = 0; i < n; i++)
        cin >> a[i];
    block = pow(n, 2.0 / 3);
    vector<qnode> query;
    for (int i = 0, cnt = 0; i < q; i++)
    {
        char op;
        cin >> op;
        if (op == 'Q')
        {
            int l, r;
            cin >> l >> r;
            query.emplace_back((qnode){l - 1, r - 1, cnt, upd.size() - 1});
            cnt++;
        }
        else
        {
            int x, y;
            cin >> x >> y;
            upd.push_back({x - 1, y});
        }
    }
    vector<int> ans(query.size());
    sort(query.begin(), query.end());
    int l = 0, r = -1, t = 0;
    stack<array<int, 2>> stk;
    for (auto &i : query)
    {
        while (l > i.l)
            add(a[--l]);
        while (r < i.r)
            add(a[++r]);
        while (l < i.l)
            del(a[l++]);
        while (r > i.r)
            del(a[r--]);
        while (t < i.t)
        {
            t++;
            if (l <= upd[t][0] && upd[t][0] <= r)
            {
                del(a[upd[t][0]]);
                add(upd[t][1]);
            }
            stk.push({upd[t][0], a[upd[t][0]]});
            a[upd[t][0]] = upd[t][1];
        }
        while (t > i.t)
        {
            if (l <= upd[t][0] && upd[t][0] <= r)
            {
                del(a[upd[t][0]]);
                add(stk.top()[1]);
            }
            a[upd[t][0]] = stk.top()[1];
            stk.pop();
            t--;
        }
        ans[i.id] = sum;
    }
    for (auto i : ans)
        cout << i << endl;
}

signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
    // cin >> t;
    while (t--)
        solve();
}

3.3 树上莫队

给定一个 $n$ 个节点的树，每个节点表示一个整数，问 $u$ 到 $v$ 的路径上有多少个不同的整数。

转成欧拉序区间问题。

具体做法：设每个点的编号 $a$ 首次出现的位置 $first[a]$ ，最后出现的位置为 $last[a]$ ，那么对于路径 $x→y$ ，设 $first[x]\le first[y]$ （不满足则swap，这个操作的意义在于，如果 $x$ 、 $y$ 在一条链上，则 $x$ 一定是 $y$ 的祖先或等于 $y$ ），如果 $lca(x,y)=x$ ，则直接把 $[first[x],first[y]]$ 的区间扯过来用，反之使用 $[last[x],first[y]]$ 区间，但这个区间内不包含 $x$ 和 $y$ 的最近公共祖先，查询的时候加上即可。

Part 4. 图论

1. 最短路

最短路，图上问题，分层图最短路，最短路形式优化 $dp$ .

最短路具有类似 $dp$ 的最优子结构性质，判定一条边 $(u,v)$ 属于最短路 $i\to j$ 的一条边，当且仅当 $dis_{i,u}+w+dis_{v,j}=dis_{i,j}$

1.1 Dijkstra

稀疏图堆优化，复杂度 $O((n+m)logn)$ ，只能处理完全正边权图。如果有负边权需要参考费用流中对偶 $Dijkstra$ ，使用势能函数进行评估。

//mlogn
#include<bits/stdc++.h>//处理完全正权有向图，可以有环
//将结点分为两类，不断松弛，但注意确定一个节点后我们便不再进行更新这个节点了（所以这是dij的短视性），所以无法处理负权，因为负权可能会更新我们已加入的节点。
using namespace std;
const int N=1e5+2;
const int inf=0x3f3f3f3f;
typedef long long ll;
typedef pair<int,int> P;
int n,m,s,u,v,sum;
struct node{
    int to,val;
};
vector<vector<node> >edge;
int dis[N],vis[N];
void dijkstra(){
    memset(dis,inf,sizeof(dis));//初始化
    dis[s]=0;
    priority_queue<P,vector<P>,greater<P>>q;//小根堆启动
    q.push({0,s});//距离在前，点在后，因为pair默认先排前面的
    while(!q.empty()){
        P k=q.top();q.pop();
        if(vis[k.second])continue;
        vis[k.second]=1;
        for(auto j:edge[k.second]){
            if(dis[j.to]>dis[k.second]+j.val){
                dis[j.to]=min(dis[j.to],dis[k.second]+j.val);
                q.push({dis[j.to],j.to});
            }
        } 
        //对所有相邻顶点进行松弛，dis是到源点的距离
    }
}
int main(){
    cin>>n>>m>>s;
    edge.resize(n+1);
    for(int i=1;i<=m;i++){
        cin>>u>>v>>sum;
        edge[u].push_back({v,sum});
    }
    dijkstra();
    for(int i=1;i<=n;i++){
        if(!vis[i])cout<<(1<<31)-1<<" ";//说明不相连
        else cout<<dis[i]<<" ";
    }
}

1.2 Floyed

以 $O(n^3)$ 的方式暴力预处理所有的最短路，本质是连通矩阵的传递闭包。适合数据范围极小的大量的最短路询问操作。曾经在 $Atcoder$ 出现过。

暴力枚举顺序千万别反了。

cin>>n>>m>>s;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(i!=j)a[i][j]=inf;//初始化
            else a[i][j]=0;
    for(int i=1;i<=m;i++){
        cin>>u>>v>>sum;
        a[u][v]=min(a[u][v],sum);//应付重边
    }
    for(int k=1;k<=n;k++)//先枚举每个中间点，来更新i，j，必须先这么做
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                a[i][j]=min(a[i][j],a[i][k]+a[k][j]);//核心过程：借助每个中间点进行松弛操作
    for(int i=1;i<=n;i++){
        if(a[s][i]==inf)cout<<(1<<31)-1<<" ";//说明不相连
        else cout<<a[s][i]<<" ";
}

1.3 SPFA/Bellman-Ford

关于 $SPFA$ ——他死了。

极端条件下会被菊花图卡成 $O(nm)$ 的算法。可以用于普适性的带负边权的图，可以检测负环。

bool spfa()
{
    memset(dis, inf, sizeof(dis)); // 初始化
    memset(cnt, 0, sizeof(cnt));   // 负环计数器
    dis[s] = 0;
    vis[s] = 1; // 注意 vis数组代表在不在队列中，在这里点是可以重复入队的
    queue<int> q;
    q.push(s);
    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        vis[u] = 0; // 取出队列中的元素，故vis为0
        for (auto i : edge[u])
        {
            if (dis[i.to] > dis[u] + i.val)
            {
                cnt[i.to]++;
                if (cnt[i.to] > n)
                    return 0;
                dis[i.to] = dis[u] + i.val;
                if (vis[i.to] == 0)
                {
                    vis[i.to] = 1;
                    q.push(i.to);
                }
            }
        }
    }
    return 1;
}

判断负环方式：当一个点被松弛了超过 $n$ 次，意味着其中一定有经过它的负环。

1.4 差分约束

$x_r-x_l\le c\iff addEdge(l,r,c)$ ， $x_r-x_l\ge c\iff addEdge(r,l,-c)$

跑最短路求可行解即可，使用 $Spfa$ 跑最短路。有负环则无解。

#include <bits/stdc++.h>
using namespace std;
#define int long long
vector<vector<array<int, 2>>> con;
void addedge(int x, int y, int z)
{
    con[x].push_back({y, z});
}
vector<int> dist, vis, tot;
int n, m;
bool spfa(vector<int> &dist, int st)
{
    dist.assign(n + 1, LONG_LONG_MIN / 2);
    vis.assign(n + 1, 0);
    tot.assign(n + 1, 0);
    queue<int> q;
    dist[0] = 0;
    vis[0] = 1;
    q.push(0);
    while (!q.empty())
    { // 判负环，看上面的
        int cur = q.front();
        q.pop();
        vis[cur] = 0;
        for (auto [v, w] : con[cur])
            if (dist[cur] + w > dist[v])
            {
                dist[v] = dist[cur] + w;
                if (!vis[v])
                {
                    vis[v] = 1;
                    q.push(v);
                    tot[v]++;
                    if (tot[v] >= n)
                    {
                        return 0;
                    }
                }
            }
    }
    return 1;
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);

    cin >> n >> m;
    con.assign(n + 1, vector<array<int, 2>>());
    for (int i = 1; i <= m; i++)
    {
        int u, v, w;
        cin >> u >> v >> w;
        addedge(u, v, w);
        addedge(v, u, -w);
    }
    for (int i = 1; i <= n; i++)
        addedge(0, i, 0);
    spfa(dist, 0);
    for (int i = 1; i <= n; i++)
        cout << dist[i] << ' ';
    cout << '\n';
    return 0;
}

1.5 分层图最短路

对于特定的一些限制条件，可以通过拆分分层图，用不同图层表示不同的状态。

示例1： $k$ 次机会不消耗花费通过某条边的最短路

#include<bits/stdc++.h>//解决问题：我们有k次机会0代价的通过某条路下的最短路
//分层图：当我们使用一次机会时，相当于我们进入下一张图
using namespace std;
const int N=2*1e5+2;
const int inf=0x3f3f3f3f;
typedef pair<int,int> P;
int n,m,k,s,t,u,v,sum;
vector<P>edge[N];
int dis[N],vis[N];
void dijkstra(){//常规不必再说
    memset(dis,inf,sizeof(dis));
    dis[s]=0;
    priority_queue<P,vector<P>,greater<P>>q;
    q.push({0,s});
    while(!q.empty()){
        P k=q.top();q.pop();
        if(vis[k.second])continue;
        vis[k.second]=1;
        for(auto j:edge[k.second])dis[j.first]=min(dis[j.first],dis[k.second]+j.second),q.push({dis[j.first],j.first});
    }
}
int main(){
    cin>>n>>m>>k>>s>>t;
    s++;t++;
    for(int i=1;i<=m;i++){
        cin>>u>>v>>sum;
        u++;v++;
        edge[u].push_back({v,sum});//原始层
        edge[v].push_back({u,sum});
        for(int j=1;j<=k;j++){//一共有k+1层，某个点在每个层s，s+n,s+2n,...,s+kn
            edge[u+j*n].push_back({v+j*n,sum});//每个层都是一样的
            edge[v+j*n].push_back({u+j*n,sum});
            edge[v+(j-1)*n].push_back({u+j*n,0});//使用特权：即换层
            edge[u+(j-1)*n].push_back({v+j*n,0});
        }
    }
    for(int i=1;i<=k;i++)edge[t+(i-1)*n].push_back({t+i*n,0});//把终点从上到小连起来，这样即使没有用完n次机会我们也是从t+nk中读答案
    dijkstra();//正常跑最短路
    printf("%d",dis[t+k*n]);
}

示例2：地铁换乘问题

//坐地铁问题：一共m条线路，n个地铁站，有换乘等问题，那就建m+1*n个点，在5e5左右，因为每层图之间的边权不同所以要把站点拆开成m个，再建立虚层连接不同层代表模拟换乘的过程
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
const int N = 510000,INF = 0x3f3f3f3f;  //注意数据范围
typedef pair<int,int> P;
int n,m,s,t;
struct node{
    int to,val;
};
vector<node>edge[N];
int dis[N],vis[N];
void add(int u,int v,int w) //加边函数
{
    //cout<<u<<" "<<v<<" "<<w<<endl;
    edge[u].push_back({v,w});
}

void dijkstra(int s){
    memset(dis,INF,sizeof(dis));//初始化
    dis[s]=0;
    priority_queue<P,vector<P>,greater<P>>q;//小根堆启动
    q.push({0,s});//距离在前，点在后，因为pair默认先排前面的
    while(!q.empty()){
        P k=q.top();q.pop();
        if(vis[k.second])continue;
        vis[k.second]=1;
        for(auto j:edge[k.second]){
            if(dis[j.to]>dis[k.second]+j.val){
                //if(j.to==8)cout<<k.second<<" "<<dis[k.second]<<endl;
                dis[j.to]=min(dis[j.to],dis[k.second]+j.val);
                q.push({dis[j.to],j.to});
            }
        } 
    }
}
int main()
{
    int price,ad,num,pre,cur;
    cin >> n >> m >> s >> t;
    for(int i = 1;i <= m;i++)
    {
        cin >> price >> ad >> num;
        for(int j = 0;j <num;j++)
        {
            cin >> cur;
            if(j){
                add((i-1)*n+pre,(i-1)*n+cur,ad);    
                add((i-1)*n+cur,(i-1)*n+pre,ad);
            }
            add((i-1)*n+cur,n*m+cur,0);
            add(n*m+cur,(i-1)*n+cur,price); 
            pre = cur;  
        }
    }
    dijkstra(n*m+s);    
    if(dis[n*m+t] == INF)   
        cout << -1 << endl;
    else
        cout << dis[n*m+t] << endl;
    return 0;
}

示例3：一些相类似的移动方式集合到一起（2023澳门区域赛）

题意概括：

有一个 $n$ 个节点的环，编号 $0\to n-1$ . 你初始在 $i$ 号节点。给一个长度为 $n$ 的数组 $a$ 。你每一次可以进行以下操作：

从 $i$ 立即传送： $i\to (a_i+i)\pmod{n}$
修改当前 $a_i$ ： $a_i\to a_i+1$

给定一个 $x$ ，询问最少经过多少次操作能够从 $0$ 到达 $x$ .

这里要看你怎么看待这个修改。在 $i$ 对 $a_i$ 加 $1$ 等价于直接跳到 $a_i+i$ 后又花费一次机会向后走。因为你永远不可能走回头路，就是第二次经过 $i$ 这个点，所以这个抽象是合理的。而我们又不可能直接在原图上把所有的点全部直接串起来。

所以开一个分层图，额外新建立一个有向环模拟后跳跃这个操作，然后一次操作 $1$ 就从原图的 $i$ 向环上的 $i+a_i$ 连边。环上的点向原图的自己连一条代价为0的单向有向边。

2. 网络流

解决网络流模型问题。

2.1 MaxFlow.h

Jiangly最新最大流模板，点编号从0开始。费用流同理。

template <class T>
struct MaxFlow
{
    struct _Edge
    {
        int to;
        T cap;
        _Edge(int to, T cap) : to(to), cap(cap) {}
    };

    int n;
    std::vector<_Edge> e;
    std::vector<std::vector<int>> g;
    std::vector<int> cur, h;

    MaxFlow() {}
    MaxFlow(int n)
    {
        init(n);
    }

    void init(int n)
    {
        this->n = n;
        e.clear();
        g.assign(n, {});
        cur.resize(n);
        h.resize(n);
    }

    bool bfs(int s, int t)
    {
        h.assign(n, -1);
        std::queue<int> que;
        h[s] = 0;
        que.push(s);
        while (!que.empty())
        {
            const int u = que.front();
            que.pop();
            for (int i : g[u])
            {
                auto [v, c] = e[i];
                if (c > 0 && h[v] == -1)
                {
                    h[v] = h[u] + 1;
                    if (v == t)
                    {
                        return true;
                    }
                    que.push(v);
                }
            }
        }
        return false;
    }

    T dfs(int u, int t, T f)
    {
        if (u == t)
        {
            return f;
        }
        auto r = f;
        for (int &i = cur[u]; i < int(g[u].size()); ++i)
        {
            const int j = g[u][i];
            auto [v, c] = e[j];
            if (c > 0 && h[v] == h[u] + 1)
            {
                auto a = dfs(v, t, std::min(r, c));
                e[j].cap -= a;
                e[j ^ 1].cap += a;
                r -= a;
                if (r == 0)
                {
                    return f;
                }
            }
        }
        return f - r;
    }
    void addEdge(int u, int v, T c)
    {
        g[u].push_back(e.size());
        e.emplace_back(v, c);
        g[v].push_back(e.size());
        e.emplace_back(u, 0);
    }
    T flow(int s, int t)
    {
        T ans = 0;
        while (bfs(s, t))
        {
            cur.assign(n, 0);
            ans += dfs(s, t, std::numeric_limits<T>::max());
        }
        return ans;
    }

    std::vector<bool> minCut()
    {
        std::vector<bool> c(n);
        for (int i = 0; i < n; i++)
        {
            c[i] = (h[i] != -1);
        }
        return c;
    }

    struct Edge
    {
        int from;
        int to;
        T cap;
        T flow;
    };
    std::vector<Edge> edges()
    {
        std::vector<Edge> a;
        for (int i = 0; i < e.size(); i += 2)
        {
            Edge x;
            x.from = e[i + 1].to;
            x.to = e[i].to;
            x.cap = e[i].cap + e[i + 1].cap;
            x.flow = e[i + 1].cap;
            a.push_back(x);
        }
        return a;
    }
};

2.2 MinCostFlow.h

支持负数费用，不支持负数流量。

/*
 *@brief 费用流（Jiangly）
 *@note 时间复杂度O(F(n+m)log(n+m)),F(n+m)表示流量和，n表示点数，m表示边数
 *@note 空间复杂度O(n+m)
 *@tparam Cap 流量数据类型
 *@tparam Cost 费用数据类型
 *@note  复杂度估算可同最大流，点数不超过2000，最坏上界估算O(n^3)到O(n^4)，基本不会TLE
 */
template <class T>
struct MinCostFlow
{
    struct _Edge
    {
        int to;
        T cap;
        T cost;
        _Edge(int to_, T cap_, T cost_) : to(to_), cap(cap_), cost(cost_) {}
    };
    int n;
    std::vector<_Edge> e;
    std::vector<std::vector<int>> g;
    std::vector<T> h, dis;
    std::vector<int> pre;
    bool dijkstra(int s, int t)
    {
        dis.assign(n, std::numeric_limits<T>::max());
        pre.assign(n, -1);
        std::priority_queue<std::pair<T, int>, std::vector<std::pair<T, int>>, std::greater<std::pair<T, int>>> que;
        dis[s] = 0;
        que.emplace(0, s);
        while (!que.empty())
        {
            T d = que.top().first;
            int u = que.top().second;
            que.pop();
            if (dis[u] != d)
            {
                continue;
            }
            for (int i : g[u])
            {
                int v = e[i].to;
                T cap = e[i].cap;
                T cost = e[i].cost;
                if (cap > 0 && dis[v] > d + h[u] - h[v] + cost)
                {
                    dis[v] = d + h[u] - h[v] + cost;
                    pre[v] = i;
                    que.emplace(dis[v], v);
                }
            }
        }
        return dis[t] != std::numeric_limits<T>::max();
    }
    MinCostFlow() {}
    MinCostFlow(int n_)
    {
        init(n_);
    }
    void init(int n_)
    {
        n = n_;
        e.clear();
        g.assign(n, {});
    }
    void addEdge(int u, int v, T cap, T cost)
    {
        g[u].push_back(e.size());
        e.emplace_back(v, cap, cost);
        g[v].push_back(e.size());
        e.emplace_back(u, 0, -cost);
    }
    std::pair<T, T> flow(int s, int t)
    {
        T flow = 0;
        T cost = 0;
        h.assign(n, 0);
        while (dijkstra(s, t))
        {
            for (int i = 0; i < n; ++i)
            {
                h[i] += dis[i];
            }
            T aug = std::numeric_limits<int>::max();
            for (int i = t; i != s; i = e[pre[i] ^ 1].to)
            {
                aug = std::min(aug, e[pre[i]].cap);
            }
            for (int i = t; i != s; i = e[pre[i] ^ 1].to)
            {
                e[pre[i]].cap -= aug;
                e[pre[i] ^ 1].cap += aug;
            }
            flow += aug;
            cost += aug * h[t];
        }
        return std::make_pair(flow, cost);
    }
    struct Edge
    {
        int from;
        int to;
        T cap;
        T cost;
        T flow;
    };
    std::vector<Edge> edges()
    {
        std::vector<Edge> a;
        for (int i = 0; i < e.size(); i += 2)
        {
            Edge x;
            x.from = e[i + 1].to;
            x.to = e[i].to;
            x.cap = e[i].cap + e[i + 1].cap;
            x.cost = e[i].cost;
            x.flow = e[i + 1].cap;
            a.push_back(x);
        }
        return a;
    }
};

2.3 Dinic (朱)

// 理论上界为n2m，处理1e4-1e5的数据
// 三个优化：多路增广，当前弧，炸点
// 少做几次bfs，一次dfs进行多次增广
// 建图时不用考虑点的变化，过程中没有用到点数这个信息，只需把边建出来就能跑
// 多测的时候记得清空e[0]
// 检查这条边是不是满流：是的话这条边的len变成0（没有剩余流量）
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 10010, M = 200010, INF = 1e15;
struct edge
{
    int ed;
    int len;
    int id;
};
vector<edge> e[N];
int n, m, S, T;
int dep[N], cur[N];
bool bfs() // bfs分层
{
    memset(dep, -1, sizeof dep);
    queue<int> q;
    q.push(S);
    dep[S] = 0;
    while (!q.empty())
    {
        int t = q.front();
        q.pop();
        for (int i = 0; i < e[t].size(); i = i + 1)
        {
            int ed = e[t][i].ed;
            if (dep[ed] == -1 && e[t][i].len) // 如果这个点没有被定义层次，且还有剩余流量
            {
                dep[ed] = dep[t] + 1;
                q.push(ed);
            }
        }
    }
    memset(cur, 0, sizeof(cur));
    if (dep[T] == -1)
        return 0;
    else
        return 1;
}
int dfs(int st, int limit) // limit最大可增加的流量
{
    if (st == T)
        return limit;
    int nowflow = 0;                                   // 定义当前节点的流量,多路增广优化，找满当前能找的limit流量上界
    for (int i = cur[st]; i < e[st].size(); i = i + 1) // 当前弧优化，如果一个点有很多出边，有些出边可能无法再推流了，我们就记录第一条可以推流的边
    {
        cur[st] = i; // 当前弧优化
        int ed = e[st][i].ed;
        if (dep[ed] == dep[st] + 1 && e[st][i].len) // 这条边能推且，深度为更深一层（为了找最短的增广路）
        {
            int t = dfs(ed, min(e[st][i].len, limit - nowflow)); // 是为了限制后面点的流量不能大于limit-nowflow
            if (t)                                               // 走下去能推流
            {
                e[st][i].len -= t;           // 减去相应的
                e[ed][e[st][i].id].len += t; // 反边+相应的
                nowflow += t;
                if (nowflow == limit)
                    return nowflow;
            }
        }
    }
    if (!nowflow)
        dep[st] = -1; // 如果这个点不能延申，那就删掉这个点（炸点优化）
    return nowflow;   // 会返回本次bfs（）后所有增广路能加的最多流量
}
int dinic()
{
    int r = 0;
    while (bfs())
        r += dfs(S, INF);
    return r;
}
void add(int u, int v, int w)
{ // cout<<u<<" "<<v<<" "<<w<<endl;
    int sti = e[u].size();
    int edi = e[v].size();
    e[u].push_back((edge){v, w, edi}); // 建边
    e[v].push_back((edge){u, 0, sti});
}
signed main()
{
    cin >> n >> m >> S >> T;
    for (int i = 1; i <= m; i++)
    {
        int u, v, w;
        cin >> u >> v >> w;
        add(u, v, w);
    }
    cout << dinic();
    return 0;
}

2.4 ISAP (朱)

// 理论上界为n2m，处理1e4-1e5的数据
// 只做一次bfs
// 建图时注意n的改变，运行过程中有跟点数相关
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 10010, INF = 1e15;
struct edge
{
    int ed;
    int len;
    int id;
};
vector<edge> e[N];
int n, m, S, T;
int dep[N], gap[N], cur[N];
void bfs() // bfs分层
{
    memset(dep, -1, sizeof dep);
    memset(gap, 0, sizeof(gap));
    queue<int> q;
    q.push(T);
    dep[T] = 0; // T为层数为0的点
    gap[0] = 1; // 层数为0的点有一个
    while (!q.empty())
    {
        int t = q.front();
        q.pop();
        for (int i = 0; i < e[t].size(); i++)
        {
            int ed = e[t][i].ed;
            if (dep[ed] == -1) // 如果这个点没有被定义层次就考虑（在这里不在乎这条边的流量是否为0！只负责分层)
            {
                dep[ed] = dep[t] + 1;
                gap[dep[ed]]++;
                q.push(ed);
            }
        }
    }
    return;
}
int dfs(int st, int limit) // limit最大可增加的流量
{
    if (st == T)
        return limit;
    int nowflow = 0;                                   // 定义当前节点的流量,多路增广优化，找满当前能找的limit流量上界
    for (int i = cur[st]; i < e[st].size(); i = i + 1) // 当前弧优化，如果一个点有很多出边，有些出边可能无法再推流了，我们就记录第一条可以推流的边
    {
        cur[st] = i; // 当前弧优化
        int ed = e[st][i].ed;
        if (dep[ed] + 1 == dep[st] && e[st][i].len) // 这条边能推且，深度为更深一层（为了找最短的增广路）
        {
            int t = dfs(ed, min(e[st][i].len, limit - nowflow)); // 是为了限制后面点的流量不能大于limit-nowflow
            if (t)                                               // 走下去能推流
            {
                e[st][i].len -= t;           // 减去相应的
                e[ed][e[st][i].id].len += t; // 反边+相应的
                nowflow += t;
                if (nowflow == limit)
                    return nowflow;
            }
        }
    } // 到这说明这个点还有剩余流量，层数就+1
    --gap[dep[st]];
    if (gap[dep[st]] == 0)
        dep[S] = n + 1; // 出现断层，无法到达t了，直接结束
    dep[st]++;          // 层++
    gap[dep[st]]++;
    return nowflow; // 会返回本次bfs（）后所有增广路能加的最多流量
}
int ISAP()
{
    int flow = 0;
    bfs();
    while (dep[S] < n)
    {
        memset(cur, 0, sizeof(cur)); // 每一次开始dfs前都要注意cur数组的清空！与dinic不同，因为这里只需要一次bfs
        flow += dfs(S, INF);         // 初始流量为无穷大
    }
    return flow;
}
void add(int u, int v, int w)
{ // cout<<u<<" "<<v<<" "<<w<<endl;
    int sti = e[u].size();
    int edi = e[v].size();
    e[u].push_back((edge){v, w, edi}); // 建边
    e[v].push_back((edge){u, 0, sti});
}
signed main()
{
    cin >> n >> m >> S >> T;
    for (int i = 1; i <= m; i++)
    {
        int u, v, w;
        cin >> u >> v >> w;
        int sti = e[u].size();
        int edi = e[v].size();
        e[u].push_back((edge){v, w, edi}); // 建边
        e[v].push_back((edge){u, 0, sti});
    }
    cout << ISAP();
    return 0;
}

2.5 预流推进（AmiyaCast）

#include <bits/stdc++.h>
#define ll long long
#define pii make_pair
const ll inf = 1145141919810;
using namespace std;
int n, m, s, t;
struct Dinic
{
    int tp, s, t, n, m;
    struct Edge
    {
        int u, v;
        ll cap;
    };
    vector<ll> dis;
    vector<int> cur, que;
    vector<vector<int>> v;
    vector<Edge> e, _e;
    Dinic(int _n, int _s, int _t)
    {
        n = _n, s = _s, t = _t;
        dis.resize(_n + 1), cur.resize(_n + 1), que.resize(_n + 1),
            v.resize(n + 1);
    }
    void add(int x, int y, ll w) { _e.push_back({x, y, w}); }
    void Add(int x, int y, int flw)
    {
        e.push_back(Edge{x, y, flw}), e.push_back(Edge{y, x, 0});
        v[x].push_back(e.size() - 2);
    }
    int bfs()
    {
        dis.assign(n + 1, inf);
        int l = 1, r = 1;
        que[1] = s, dis[s] = 0;
        while (l <= r)
        {
            int p = que[l++], to;
            for (int i : v[p])
                if (e[i].cap && dis[to = e[i].v] >= inf)
                    dis[to] = dis[p] + 1, que[++r] = to;
        }
        return dis[t] < inf;
    }
    int dfs(int p, ll a)
    {
        if (p == t || !a)
            return a;
        int sf = 0, flw;
        for (int &i = cur[p], to; i < (int)v[p].size(); ++i)
        {
            Edge &E = e[v[p][i]];
            if (dis[to = E.v] == dis[p] + 1 && (flw = dfs(to, min(a,
                                                                  E.cap))))
            {
                E.cap -= flw;
                e[v[p][i] ^ 1].cap += flw;
                a -= flw;
                sf += flw;
                if (!a)
                    break;
            }
        }
        return sf;
    }
    ll dinic(int tp = 1)
    {
        this->tp = tp;
        int flw = 0;
        while (bfs())
            cur.assign(n + 1, 0), flw += dfs(s, inf);
        return flw;
    }
    ll get_ans()
    {
        ll ans = 0;
        m = _e.size();
        sort(_e.begin(), _e.end(), [](Edge a, Edge b)
             { return a.cap >
                      b.cap; });
        for (int rp = 0; rp <= 1; ++rp)
            for (int p = 1 << 30, i = 0; p; p /=
                                            2)
            {
                for (; i < m && _e[i].cap >= p; ++i)
                    if (rp)
                        v[_e[i].v].push_back(i * 2 + 1);
                    else
                        Add(_e[i].u, _e[i].v, _e[i].cap);
                ans += dinic(rp);
            }
        return ans;
    }
};
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin >> n >> m >> s >> t;
    Dinic d(n, s, t);
    for (int i = 0; i < m; i++)
    {
        int x, y;
        ll w;
        cin >> x >> y >> w;
        d.add(x, y, w);
    }
    cout << d.get_ans() << endl;
    return 0;
}

2.6 最小费用最大流（朱）

//理论上界为n2m，处理1e4-1e5的数据
//每条边流过去多了一个成本
//bfs换成了spfa跑最短路即可,0号点得空出来
//最大费用最大流：建边时把c反着建，照样跑板子，最后答案也反过来就行，类似最长路
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 10010, M = 200010, INF = 1e15;
struct edge
{
    int ed;
    int len;
    int id;
    int cost;
};
vector <edge> e[N];
int n, m, S, T;
int dep[N], dis[N], vis[N],ans ,res;
bool spfa(){
    memset(dis,0x3f,sizeof(dis));//初始化
    memset(vis,0,sizeof(vis));
    dis[T]=0;
    vis[T]=1;//vis数组代表在不在队列中
    deque<int>q;q.push_back(T);
    while(!q.empty()){
        int u=q.front();q.pop_front();
        vis[u]=0;//取出队列中的元素，故vis为0
        for (int i = 0; i < e[u].size(); i++){
            int ed = e[u][i].ed;
            if (e[ed][e[u][i].id].len && dis[ed]>dis[u]-e[u][i].cost){//取反向边是因为我们要保证正流，但是SPFA是倒着跑的，所以说我们要求e[u][i]的对应反向边是正的，
                dis[ed]=dis[u]-e[u][i].cost;
                if (!vis[ed]){
                    vis[ed]=true;
                    if (q.empty() || dis[ed]>=dis[q.front()])q.push_back(ed);//一个lis优化spfa的
                        else q.push_front(ed);
                }
            }
        }
    }
    return dis[S]<dis[0];
}
int dfs(int st, int limit){
    vis[st]=1;
    if (st == T||limit==0)
        return limit;
    int nowflow=0;//定义当前节点的流量
    for (int i = 0; i < e[st].size(); i = i + 1){
        int ed = e[st][i].ed;
        if (dis[ed] == dis[st] - e[st][i].cost && e[st][i].len&&!vis[ed])//这条边能推且，深度为更深一层，且没走过
        {
            int t = dfs(ed, min(e[st][i].len, limit-nowflow));//是为了限制后面点的流量不能大于limit-nowflow
            if (t)//走下去能推流
            {
                res+=t*e[st][i].cost;//统计答案，经过这一条边
                e[st][i].len -= t;
                e[ed][e[st][i].id].len += t;
                nowflow+=t;
                if(nowflow==limit)return nowflow;
            }

        }
    }
    if(!nowflow)dep[st]=-1;//如果这个点不能延申，那就删掉这个点（炸点优化）
    return nowflow;//会返回本次bfs（）后所有增广路能加的最多流量
}
void dinic(){
    while(spfa()){
        vis[T]=1;
        while(vis[T]){//如果dfs完已经走不到t了那说明这一轮结束
            memset(vis,0,sizeof vis);
            ans+=dfs(S,INF);
        }
    }
}
void add(int u,int v,int w,int c){
    //cout<<u<<" "<<v<<" "<<w<<endl;
    int sti = e[u].size();
    int edi = e[v].size();
    e[u].push_back((edge){v, w, edi, c});//建边
    e[v].push_back((edge){u, 0, sti, -c});
}
signed main(){
    cin>>n>>m>>S>>T;
    for (int i = 1; i <= m; i++){
        int u,v,w,c;
        cin >> u >> v >> w >> c;
        int sti = e[u].size();
        int edi = e[v].size();
        e[u].push_back((edge){v, w, edi, c});//建边
        e[v].push_back((edge){u, 0, sti, -c});
    }
    dinic();
    cout<<ans<<" "<<res;
    return 0;
}

2.7 网络流结论

2.7.1 二分图博弈

二分图博弈，给出一张二分图和起始点 H，A 和 B轮流操作，每次只能选与上个被选择的点（第一回合则是点 H）相邻的点，且不能选择已选择过的点，无法选点的人输掉。

具体来说，就是所有的状态可以被分为两类，每次操作必定是从一个状态到另一类状态，不能操作的人输

做法，如果二分图的所有最大匹配都经过H，那么先手必胜，否则必败

建图后判断H是不是必须点即可（跑两次，第一次不带H点，跑一次，再带上H点，看看能不能有新增流量，若有则是必须点，先手必胜，否则必败）

void solve(){
    cin>>m>>n>>s;
    for (int i = 0; i < N; i++)e[i].clear();
    memset(sp,0,sizeof(sp));
    int M=a[m];S=M+1;T=M+2;
    for (int i = 1; i <= n; i++) {
        int x ;cin>>x; sp[x] = 1;//禁止访问的状态
    }
    for(int i = 0; i < M; i++) {//每个状态
        if(sp[i]) continue;
        if(odd[i] == odd[s]) {
            calc(i);//i的后继状态连边
            if (i != s) add(S, i, 1);//起点先不连
        }
        else {
            add(i, T, 1);   
        }
    }
    dinic();//如何判断这个点是不是最大匹配的必须点？先不加这个点跑一次，再加上跑一次，看能不能有新流即可
    add(S, s, 1);
    if(dinic())
        cout<<"Alice"<<endl;
    else 
        cout<<"Bob"<<endl;
}

2.7.2 最小路径覆盖与偏序集合Dilworth定理

2.7.2.1 最小路径覆盖

最小路径覆盖问题是指用最少的不相交路径，使得路径覆盖整个有向图的所有点。

本质是二分图的最大匹配。

目标是覆盖所有的点，这些路径不要求非得共用起点和终点。初始考虑每个点都被一条自环唯一覆盖，那么一条边连通两个点就意味着这条边同时覆盖了这两个点，同时因为不相交路径的属性确保了如果点 $A$ 连向了点 $B$ ，那么一定不会再有点 $A$ 连向任何一个点。确保一个点只连接一条出边，就是二分图的最大匹配问题。建图跑最大匹配后找出最大可化简数量，结果就是 $n-$ 最大流。

示例1：（模板题)

给定有向图 $G=(V,E)$ 。设 $P$ 是 $G$ 的一个简单路（顶点不相交）的集合。如果 $V$ 中每个定点恰好在 $P$ 的一条路上，则称 $P$ 是 $G$ 的一个路径覆盖。 $P$ 中路径可以从 $V$ 的任何一个定点开始，长度也是任意的，特别地，可以为 $0$ 。 $G$ 的最小路径覆盖是 $G$ 所含路径条数最少的路径覆盖。设计一个有效算法求一个 DAG（有向无环图） $G$ 的最小路径覆盖。

输入格式

第一行有两个正整数 $n$ 和 $m$ 。 $n$ 是给定 DAG（有向无环图） $G$ 的顶点数， $m$ 是 $G$ 的边数。接下来的 $m$ 行，每行有两个正整数 $i$ 和 $j$ 表示一条有向边 $(i,j)$ 。

输出格式

从第一行开始，每行输出一条路径。文件的最后一行是最少路径数。

对于 $100\%$ 的数据， $1\leq n\leq 150$ ， $1\leq m\leq 6000$ 。

记录路径在dfs中维护一个nxt数组表示这个点的下一个。

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 10010, M = 200010, INF = 1e15;
struct edge
{
    int ed;
    int len;
    int id;
};
vector<edge> e[N];
int n, m, S, T;
int dep[N], cur[N], p[N], net[N], d[N];
bool bfs() // bfs分层
{
    memset(dep, -1, sizeof dep);
    queue<int> q;
    q.push(S);
    dep[S] = 0;
    while (!q.empty())
    {
        int t = q.front();
        q.pop();
        for (int i = 0; i < e[t].size(); i = i + 1)
        {
            int ed = e[t][i].ed;
            if (dep[ed] == -1 && e[t][i].len) // 如果这个点没有被定义层次，且还有剩余流量
            {
                dep[ed] = dep[t] + 1;
                q.push(ed);
            }
        }
    }
    memset(cur, 0, sizeof(cur));
    if (dep[T] == -1)
        return 0;
    else
        return 1;
}
int dfs(int st, int limit) // limit最大可增加的流量
{
    if (st == T)
        return limit;
    int nowflow = 0;                                   // 定义当前节点的流量,多路增广优化，找满当前能找的limit流量上界
    for (int i = cur[st]; i < e[st].size(); i = i + 1) // 当前弧优化，如果一个点有很多出边，有些出边可能无法再推流了，我们就记录第一条可以推流的边
    {
        cur[st] = i; // 当前弧优化
        int ed = e[st][i].ed;
        if (dep[ed] == dep[st] + 1 && e[st][i].len) // 这条边能推且，深度为更深一层（为了找最短的增广路）
        {
            int t = dfs(ed, min(e[st][i].len, limit - nowflow)); // 是为了限制后面点的流量不能大于limit-nowflow
            if (t)                                               // 走下去能推流
            {
                e[st][i].len -= t;           // 减去相应的
                e[ed][e[st][i].id].len += t; // 反边+相应的
                nowflow += t;
                if (t)
                    net[st] = ed - n;
                if (nowflow == limit)
                    return nowflow;
            }
        }
    }
    if (!nowflow)
        dep[st] = -1; // 如果这个点不能延申，那就删掉这个点（炸点优化）
    return nowflow;   // 会返回本次bfs（）后所有增广路能加的最多流量
}
int dinic()
{
    int r = 0;
    while (bfs())
        r += dfs(S, INF);
    return r;
}
void add(int u, int v, int w)
{
    // cout<<u<<" "<<v<<" "<<w<<endl;
    int sti = e[u].size();
    int edi = e[v].size();
    e[u].push_back((edge){v, w, edi}); // 建边
    e[v].push_back((edge){u, 0, sti});
}
void print(int x)
{
    printf("%d ", x);
    if (net[x] > 0)
        print(net[x]);
}
signed main()
{
    cin >> n >> m;
    S = 0;
    T = 2 * n + 1;
    for (int i = 1; i <= m; i++)
    {
        int u, v;
        cin >> u >> v;
        add(u, v + n, 1);
    }
    for (int i = 1; i <= n; i++)
    {
        add(S, i, 1);
        add(i + n, T, 1);
    }
    int maxflow = dinic();
    for (int i = 1; i <= n; i++)
        if (net[i])
            d[net[i]]++;
    for (int i = 1; i <= n; i++)
        if (!d[i])
            print(i), cout << endl;
    cout << n - maxflow;
    return 0;
}

2.7.2.2 Dilworth定理

根据 $Dilworth$ 定理，偏序集合的最长链长度等于其最小的反链覆盖。

链：一条链是一些点的集合，点集中任意两个点 $u$ 和 $v$ ，满足 $u$ 能到达 $v$ 或是 $v$ 能到达 $u$ （存在偏序关系），则称该点集为一条链。

反链：一条反链是一些点的集合，点集中任意两个点 $u$ 和 $v$ ，满足 $u$ 不能到达 $v$ 并且 $v$ 不能到达 $u$ ，则称该点集为一条反链。

最小链覆盖是指在有向图中用可以相交的若干条路径覆盖整个图且路径数最少。

求出有向图的传递闭包之后即可按照示例一不相交路径求解，二分图最大匹配即可。

如果有向图是一个完备的偏序集合哈斯图（即其传递闭包等于自身），则最小链覆盖等价于最小路径覆盖。此时， $Dilworth$ 定理可重新表述为最大链长度等于最小的反链划分。

示例1：ABC237Ex Hakata

我们有一个由小写英文字母组成的字符串 $S$ 。Bob 每天都在思考回文。他决定从 $S$ 中选择一些回文子串并告诉 Anna。

如果 Bob 告诉的回文之一是另一个回文的子串，Anna 会生气。Bob 可以选择最多多少个回文而不会让 Anna 生气？

$N\le 300$

显然，包含是一个偏序关系。我们要求解的是最长的互相不包含的回文串序列长度，实际上就是最长的反链长度。

$Dilworth$ 定理转最小的反链覆盖。由于我们能够建立出完备的偏序哈斯图（实际上都可以），又转最小反链划分，即最小路径覆盖。

求二分图最大匹配，参考示例1，作差即可。

void solve()
{
    string s;
    cin >> s;
    vector<string> pali;
    for (int i = 0; i < s.size(); i++)
    {
        for (int j = 1; i + j <= s.size(); j++)
        {
            string t = s.substr(i, j);
            string r = t;
            reverse(r.begin(), r.end());
            if (t == r)
            {
                pali.push_back(t);
            }
        }
    }
    sort(pali.begin(), pali.end());
    pali.erase(unique(pali.begin(), pali.end()), pali.end());
    int sz = pali.size();
    MaxFlow<int> mf(2 * sz + 10);
    const int S = 2 * sz, T = 2 * sz + 1;
    for (int i = 0; i < sz; i++)
    {
        mf.addEdge(S, i, 1);
        mf.addEdge(sz + i, T, 1);
    }
    for (int i = 0; i < sz; i++)
    {
        for (int j = 0; j < sz; j++)
        {
            if (i == j)
                continue;
            if (pali[i].find(pali[j]) != string::npos)
            {
                mf.addEdge(i, sz + j, 1);
            }
        }
    }
    cout << sz - mf.flow(S, T) << endl;
}

2.7.3 最大流最小割定理

最大流=最小割。

割集好比是一个恐怖分子把你家和自来水厂之间的水管网络砍断了一些然后自来水厂无论怎么放水水都只能从水管断口哗哗流走了你家就停水了割的大小应该是恐怖分子应该关心的事毕竟细管子好割一些而最小割花的力气最小

网络的最大流等于最小割

具体的证明分三部分

任意一个流都小于等于任意一个割。

这个很好理解，自来水公司随便给你家通点水构成一个流，恐怖分子随便砍几刀，砍出一个割，由于容量限制，每一根的被砍的水管子流出的水流量都小于管子的容量，每一根被砍的水管的水本来都要到你家的，现在流到外面，加起来得到的流量还是等于原来的流。管子的容量加起来就是割，所以流小于等于割。由于上面的流和割都是任意构造的，所以任意一个流小于任意一个割。

构造出一个流等于一个割。

当达到最大流时，根据增广路定理，残留网络中 $s$ 到 $t$ 已经没有通路了，否则还能继续增广。我们把 $s$ 能到的的点集设为 $S$ ，不能到的点集为 $T$ ，构造出一个割集 $C[S,T]$ ， $S$ 到 $T$ 的边必然满流，否则就能继续增广，这些满流边的流量和就是当前的流即最大流。把这些满流边作为割，就构造出了一个和最大流相等的割。

最大流等于最小割。

设相等的流和割分别为 $F_m$ 和 $C_m$ ，则因为任意一个流小于等于任意一个割，任意 $F≤Fm=Cm≤$ 任意 $C$ 。

2.7.4 最大权闭合子图

最大权闭合子图：给定一个有向图, 顶点带权值. 你可以选中一些顶点, 要求当选中一个点 $u$ 的时候, 若存在边 $u\rightarrow v$ 则 $v$ 也必须选中. 最大化选中的点的总权值.

建模：负点权点向重点连边，源点向正点权点连边，图中原先的点连无穷大边，跑最小割即可，最终结果就是所有正点权之和 $-$ 最小割。

示例：CFedu171 Best Subsequence

给定一个整数数组 $$a$$ ，大小为 $n$ 。

我们将数组的值定义为其大小减去数组所有元素按位或中的设置位数。

例如，对于数组 $[1, 0, 1, 2]$ ，按位或为 $3$ (包含 $2$ 个设置位)，数组的值为 $$4-2=2$$ 。

您的任务是计算给定数组的某个子序列的最大可能值。

显然是最大权闭合子图问题，或者可以理解为二者选其一问题。该点要被选择，这些位置都要被扣1.

void solve()
{
    int n;
    cin >> n;
    vector<i64> a(n);
    for (int i = 0; i < n; i++)
    {
        cin >> a[i];
    }
    MaxFlow<i64> f;
    int sz = n + 60 + 2;
    f.init(sz);
    const int s = n + 60, t = n + 60 + 1;
    for (int i = 0; i < n; i++)
    {
        f.addEdge(s, i, 1);
        for (int j = 59; j >= 0; j--)
        {
            if ((a[i] >> j) & 1)
            {
                f.addEdge(i, n + j, 1);
            }
        }
    }
    for (int j = 59; j >= 0; j--)
    {
        f.addEdge(n + j, t, 1);
    }
    i64 ans = f.flow(s, t);
    cout << n - ans << endl;
}

2.7.5 二者选其一问题

将若干元素 $e_1,e_2,…,e_n$ 划分到两个集合 $A,B$ 中。对于元素 $e_i$ ,它被划分到 $A$ 或 $B$ 中分别能获得一个 $a_{e_i}$ 或 $b_{e_i}$ 的分值。除此之外,还给出若干个组合 $C_i\in E$ ,当组合中的元素被同时划分到 $A$ 或 $B$ 时,可以获得额外的分值 $a'$ 或 $b'$ 。求最大的分值。

基本模型是设立两个超级源点，每个物品分别连，最大收益就是收益总和-最小割

对于同属于一遍的额外组合，则新建节点，超级源点（以 $A$ 示例）向该新节点流额外收益 $a'$ ，为保证后续节点必定在 $A$ 部，该新节点向该组合的中间点连无穷大边，迫使最小割如果保留了 $a'$ 边，就必须隔断所有和 $B$ 的边，以达成正确性。

示例：2024杭电多校（5）猫咪们狂欢

猫咪们生活在树上。

具体来说，有 $n$ 只猫咪和两棵大小为 $n$ 的树。猫咪编号为 $1∼n$ ，每棵树上的节点编号也为 $1∼n$ （编号各不相同）。

今晚，每只猫咪要分别选择一棵树，并待在与其编号相同的节点。

在这 $n$ 只猫咪之中，有 $k$ 只猫咪是狂欢猫。狂欢猫晚上不会睡觉，而是会选择开party。其他猫咪则会选择睡觉。

每条树边都有一个狂欢值，如果这条边连接的两个节点在晚上都有狂欢猫待着，这个狂欢值就会被累加到总狂欢值上。

最大化今晚的总狂欢值，并输出这个值。

显然是二者选其一问题，每只猫咪有选择左还是选择右的问题，有最多 $n-1$ 组组合会有额外收益。狂欢猫只有 $k$ 只，涉及到的狂欢猫才形成组队节点。

void solve()
{
    int n, k;
    cin >> n >> k;
    vector<int> cat(k + 1);
    map<int, int> mp;
    for (int i = 1; i <= k; i++)
    {
        cin >> cat[i];
        mp[cat[i]] = 1;
    }
    const int s = 0, t = n + 1;
    MaxFlow<i64> flow(4 * n + 10);
    int virp = n + 2;
    i64 ans = 0;
    for (int i = 1; i < n; i++)
    {
        int u, v, w;
        cin >> u >> v >> w;
        if (mp[u] && mp[v])
        {
            flow.addEdge(s, virp, w);
            flow.addEdge(virp, u, INT_MAX / 2);
            flow.addEdge(virp, v, INT_MAX / 2);
            ans += w;
            virp++;
        }
    }
    for (int i = 1; i < n; i++)
    {
        int u, v, w;
        cin >> u >> v >> w;
        if (mp[u] && mp[v])
        {
            flow.addEdge(virp, t, w);
            flow.addEdge(u, virp, INT_MAX / 2);
            flow.addEdge(v, virp, INT_MAX / 2);
            ans += w;
            virp++;
        }
    }
    cout << ans - flow.flow(s, t) << endl;
}

2.7.6 二分图最大边权匹配

二分图的最大权匹配是指二分图中边权和最大的匹配。数据保证有解。

考虑费用流。

与 二分图最大匹配类似，二分图的最大权匹配也可以转化为网络流问题来求解。

首先，在图中新增一个源点和一个汇点。

从源点向二分图的每个左部点连一条流量为 $1$ ，费用为 $0$ 的边，从二分图的每个右部点向汇点连一条流量为 $1$ ，费用为 $0$ 的边。

接下来对于二分图中每一条连接左部点 $u$ 和右部点 $v$ ，边权为 $w$ 的边，则连一条从 $u$ 到 $v$ ，流量为 $1$ ，费用为 $w$ 的边。

另外，考虑到最大权匹配下，匹配边的数量不一定与最大匹配的匹配边数量相等（不一定最大流），因此对于每个左部点，还需向汇点连一条流量为 $1$ ，费用为 $0$ 的边。

求这个网络的 最大费用最大流即可得到答案。此时，该网络的最大流量一定为左部点的数量，而最大流量下的最大费用即对应一个最大权匹配方案。最大费用最大流可以直接负费用的最小费，Jiangly模板支持。

2.7.7 二分图最小边权点覆盖

二分图的最小边权点覆盖指找到一个边权和最小的顶点覆盖。数据保证有解。

考虑最小覆盖的一种构造方式：

选择一个匹配边集合 $E_1$ ，所有不属于 $E_1$ 包含的点集 $V_1$ 的点选择一条与自己相邻的点中边权最小的那一个点，添加对应边（允许重边）。可以证明最优解一定可以被这种构造方式构造，且是否是最优解一定取决于 $E_1$ 的选择。

设点 $u$ 为端点的边的最小边权为 $wm_u$ ，则有一个非常简单的化简：

$Cost=\sum_{e\in E_1}c(e)+\sum_{v\in V\backslash V_1}wm_v=\sum_{v\in V}wm_v+\sum_{e\in E_1}(c(e_{u,v})-wm_u-wm_v)$

最小化第二项成本即可。构建以下网络流二分图跑最小费用流：

从 $S$ 向每个 $X_i$ 添加一条边，容量为 $1$ ，成本为 $0$
对于每个 $(X_i,Y_j)$ ，从 $X_i$ 向 $Y_j$ 添加一条边，容量为 $1$ ，成本为 $(c(e_{X_i,Y_i})-wm_{X_i}-wm_{Y_i})$
从每个 $Y_i$ 向 $T$ 添加一条边，容量为 $1$ ，成本为 $0$ .
另外，考虑到最小费匹配下，匹配边的数量不一定与最大匹配的匹配边数量相等（不一定最大流，这个带有负成本的更为明显），因此对于每个左部点，还需向汇点连一条流量为 $1$ ，费用为 $0$ 的边。

直接跑 $MincostFlow.h$ 就行，Jiangly模板支持负数费用。

示例1：ABC231H - Minimum Coloring

我们有一个网格，有 $H$ 行和 $W$ 列。令 $(i,j)$ 表示从顶部算起第 $i$ 行和从左侧算起第 $j$ 列的方格。

在这个网格上，有 $N$ 个白色棋子，编号为 $1$ 至 $N$ 。棋子 $i$ 位于 $(A_i,B_i)$ 上。

您可以支付 $C_i$ 的费用来将棋子 $i$ 改为黑色棋子。

找出在每一行和每一列中至少有一个黑色棋子所需的最小总费用。

裸的板子。

void solve()
{
    int n, m, k;
    cin >> n >> m >> k;
    const int s = n + m, t = n + m + 1;
    MinCostFlow<i64> mcf(n + m + 10);
    vector<int> a(n + m + 10, INT_MAX / 2);
    vector<array<int, 3>> e(k);
    for (int i = 0; i < k; i++)
    {
        int u, v, w;
        cin >> u >> v >> w;
        u--;
        v--;
        e[i] = {u, v, w};
        a[u] = min(a[u], w);
        a[n + v] = min(a[n + v], w);
    }
    i64 ans = 0;
    for (int i = 0; i < n; i++)
    {
        mcf.addEdge(s, i, 1, 0);
        mcf.addEdge(i, t, 1, 0);
        ans += a[i];
    }
    for (int j = 0; j < m; j++)
    {
        mcf.addEdge(n + j, t, 1, 0);
        ans += a[n + j];
    }
    for (int i = 0; i < k; i++)
    {
        auto [u, v, w] = e[i];
        mcf.addEdge(u, n + v, 1, w - a[u] - a[n + v]);
    }
    auto [flow, cost] = mcf.flow(s, t);
    cout << ans + cost << endl;
}

2.7.8 剩余物品互不相同问题

操作后剩余互不相同，可以通过列举出所有剩余物品种类之后每个只向超级汇点连一条容量为 $1$ 的边，以确保每种物品只会出现一次。

剩余数量限制为 $x$ 的时候同理，限制容量大小即可。

示例1：（2024成都站K)

您有一个神奇的集合，最初包含 $n$ 个不同的整数。您发现这些数字可以通过除以它们的因数来产生能量。在每个步骤中，您可以从集合中选择任何大于 $1$ 的数字，将其删除，然后插入它的一个因数。您插入的因数不得等于原始数字。此外，由于神奇集合的不稳定性，您的操作必须确保集合中的数字保持不同。

每个操作都会产生一个能量单位，您的目标是通过执行尽可能多的操作来最大化产生的总能量。给定集合中的初始数字，确定可以产生的最大能量，即可执行的最大操作数。

显然每个数都会尽可能的按步数分解，最大的操作数一定取决于随后剩余的因数组合问题。规约到二分图最大权匹配即可。

分解因数，超级源点向初始数连一条容量为 $1$ 、费用为 $0$ 的边；初始数字向对应因数连容量为 $1$ 、对应消耗次数的费用 $w$ ；对应因数向超级终点连容量为 $1$ 、费用为 $0$ 的边。跑最大费用流即可。

2.7.9 其他记录

1.小M的作物(最小割) 巧妙将问题转化为最小割

2.奶牛的电信Telecowmunication 最小割边转化为最小割点，方法是拆点把一个点拆成两个点，用1的边长连起来，两个不同点之间的连线用INF连起来，这样的最小割就只能割1的点，相当于割点了

3.教辅的组成也是拆点，我们限制一个点通过的流量，就是把这个点拆成两个点，中间连一条我们要限制的流量的大小的边

4.狼捉兔子可以直接网络流也可以最小割转平面图最短路（平面图最小割=对偶图的最短路）

5.方格取数问题，有条件的最值。二分图点权最大独立集

把方格根据i+j的奇偶性分为两类点，发现保留一个点的代价是取走周围的另一类的点，转化为最小割。

S连白点，容量为点权，黑点连T同理，同时一个点向周围四个点连边，边权为inf，这样跑出来的最小割，舍弃一个点为断开他与一个源点的连接，意思就是不要这个点，保留下来的点就是最大的，sum-dinic()即可

套路：方格中的点看看能不能分为两类，即分为一个二分图，同类的点是可以共存的，然后不能共存的一定是两类之间，中间连inf边跑最大流，答案就是总和减去最小割。

3. 生成树

3.1 两种最小生成树

3.1.1 Prim

void prim(){
    memset(dis,0x3f3f3f3f,sizeof(dis));
    priority_queue<node>q;//所以这里其实是小根堆，存的是边（每次抉择时待选的边）
    node t;t.to=1,t.val=0;dis[1]=0;
    q.push(t);//（最开始选择起点）
    while(q.size()!=0){
        node now=q.top();q.pop();
        if(vis[now.to]==1)continue;
        vis[now.to]=1;
        ans+=now.val;
        for(auto i:edge[now.to]){
            if(!vis[i.to]&&dis[i.to]>i.val){
                //有更新的边，都是可能要被选的边，加入队列中，这里的判断只有边权，因为dis是到当前集合的距离
                dis[i.to]=i.val;
                q.push(i);
            }
        }
    }
}

3.1.2 Kruskal

cin>>n>>m;
    for(int i=1;i<=n;i++)fa[i]=i;//并查集维护是否在生成树里
    for(int i=1;i<=m;i++){
        cin>>u>>v>>sum;
        a[i].x=u,a[i].y=v,a[i].val=sum;
    }
    sort(a+1,a+1+m);
    for(int i=1;i<=m;i++){
        if(fa[find(a[i].x)]==fa[find(a[i].y)])continue;//已经加入了那就不要了
        else{
            unions(a[i].x,a[i].y);//加边
            k++;
            ans+=a[i].val;
        }
        if(k==n-1)break;
    }
    if(k<n-1)cout<<"orz";
else cout<<ans;

*3.2 Kruskal重构树

Kruskal 重构树就是基于 Kruskal 的最小生成树算法在无向图中得出的树所构造而成的树。

性质

是一棵二叉树。
如果是按最小生成树建立的话是一个大根堆。
强大性质：原图中两个点间所有路径上的边最大权值的最小值 == 最小生成树上两点简单路径的边最大权值 == $Kruskal$ 重构树上两点 $LCA$ 的点权。

利用这个性质，我们可以找到到点 $x$ 的简单路径上的边最大权值的最小值 $≤ val$ 的所有点 $y$ 。可以发现都在 $Kruskal$ 重构树上的某一棵子树内，且恰好为该子树的所有叶节点。

具体细节

我们在 $Kruskal$ 重构树上找到 $x$ 到根的路径上权值 $≤val$ 的最浅的节点,这就是那棵子树的根节点。这个到时候类似求 $LCA$ 由高到低倍增跳就行了，一般这种情况下还有树上线段树合并或者书上主席树之类的。

如果题目要求最小权值最大值，可以建最大生成树的重构树从而达到一样的效果。

void Ex_Kruskal()
{
    int cnt=n;
    sort(e+1,e+m+1,cmp);//对边排序
    for (int i=1;i<2*n;++i) f[i]=i;//预处理并查集
    for (int i=1;i<=m;++i)
    {
        int u=get(e[i].x),v=get(e[i].y);
        if (u!=v)
        {
            ++cnt;//新点
            f[u]=f[v]=cnt;//初始化
            val[cnt]=e[i].z;//新点权为这个边权
            add(cnt,u);add(cnt,v);//连边
            if (cnt==2*n-1) break;//一共2*n-1个点，建好退出
        }
    }
}

4. 二分图最大匹配/二分图最小点覆盖

匈牙利算法，或者网络流。

匈牙利算法,判断二分图：并查集/dfs（即染色法/并查集）

二分图是什么？节点由两个集合组成，且两个集合内部没有边的图。这张图上的所有边的两个端点，都分属不同的部分，无向图

最大匹配：要求选出一些边，使得这些边没有公共顶点，且边的数量最大。

二分图中，最小点覆盖 = 最大匹配最小点覆盖：指的是在一个图中：一个点覆盖与之连接的边，求用最少的点可以覆盖图。

二分图中，最大独立集 = $n- $最小点覆盖

最大独立集：一个点集，里面的点两两不相邻

算法步骤：如果后来的和以前的发生矛盾，则以前的被绿优先退让。

如果以前的退让之后没有cp可处，则以前的拒绝退让，新来的去寻找下一个匹配。

如果新来的谁也匹配不上了，那就这么单着吧。

//O(nm),但是Dinic可以sqrt(n)*m
#include<bits/stdc++.h>
using namespace std;
const int N=2*1e5+2;
const int inf=0x3f3f3f3f;
typedef pair<int,int> P;
int n,m,e,u,v,ans;
vector<int>edge[505];
int vis[505],match[505];//match：为右部点建立的数组，存的是与它匹配的左部点
bool check(int x){
    for(auto i:edge[x]){//枚举每一个右部点
        if(!vis[i]){//没访问过
            vis[i]=1;
            if(!match[i]||check(match[i])){//可以直接匹配or原先的i可以换人
                match[i]=x;
                return 1;
            }
        }
    }
    return 0;
}
int main(){
    cin>>n>>m>>e;
    for(int i=1;i<=e;i++){
        cin>>u>>v;
        edge[u].push_back(v);
    }
    for(int i=1;i<=n;i++){
        memset(vis,0,sizeof(vis));//对于每一个u的研究，对另一外一半只能访问一次，故每次都要清空
        if(check(i))ans++;
    }
    cout<<ans;
}

5.树上问题

5.1 树上LCA

关于倍增法以及欧拉序 $ST$ 表在线做法参见数据结构部分。这里只给出离线 $Tarjan$ 算法，实现 $O(n+m)$ 复杂度。

#include<bits/stdc++.h>//Tarjan离线算法
using namespace std;
const int N=5*1e5+2;
typedef long long ll;
struct point{
    int x,i;
};
vector<vector<int> >edge;
vector<vector<point> >q;
int dep[N],fa[N],vis[N],ans[N];
int find(int x){//路径压缩
    if(fa[x]!=x){
        fa[x]=find(fa[x]);
    }
    return fa[x];
}
void unions(int x,int y){//x合并到y上
    fa[find(x)]=fa[find(y)];
}
void dfs(int x,int f){/***1.**以s为根节点，从根节点开始。
**2.**遍历该点u所有子节点v，并标记这些子节点v已被访问过。
**3.**若是v还有子节点，返回2，否则下一步。
**4.**合并v到u上。
**5.**寻找与当前点u有询问关系的点v。
**6.**若是v已经被访问过了，则可以确认u和v的最近公共祖先为v被合并到的父亲节点a。*/
    vis[x]=1;
    for(auto i:edge[x]){
        if(i!=f){
            dfs(i,x);
            unions(i,x);
        }
    }
    for(auto t:q[x]){
        if(vis[t.x])ans[t.i]=find(t.x);
    }
}
int main(){
    int n,m,s;int x,y;
    cin>>n>>m>>s;
    edge.resize(n+1);
    q.resize(n+1);
    for(int i=1;i<=n;i++)fa[i]=i;
    for(int i=1;i<n;i++){
        cin>>x>>y;
        edge[x].push_back(y);
        edge[y].push_back(x);
    }
    for(int i=1;i<=m;i++){
        cin>>x>>y;
        q[x].push_back({y,i});//另一个相关点和组数
        q[y].push_back({x,i});
    }
    dfs(s,0);
    for(int i=1;i<=m;i++)cout<<ans[i]<<endl;
    return 0;
}

/*一个熊孩子Link从一棵有根树的最左边最底下的结点灌岩浆，Link表示很讨厌这种倒着长的树。
岩浆会不断的注入，直到注满整个树…
如果岩浆灌满了一棵子树，Link发现树的另一边有一棵更深的子树，Link会先去将那棵子树灌满。
岩浆只有在迫不得已的情况下才会向上升高，找到一个新的子树继续注入。
机(yu)智(chun)的Link发现了找LCA的好方法，即如果两个结点都被岩浆烧掉时，他们的LCA即为那棵子树上岩浆最高的位置*/

5.2 树链剖分

参见数据结构部分静态树章节，对于长链、重链都有。

这里贴出重链剖分头文件 $HLD.h$ 。这个是从 $0$ 开始的。

/*
     *@brief 重链剖分(jiangly)版本
     *@brief 时间复杂度O(n)
     *@brief 空间复杂度O(n)
     */
    struct HLD
    {
        int n;
        std::vector<int> siz, top, dep, parent, dfn, enddfn, rk;
        std::vector<std::vector<int>> adj;
        int cur;
        HLD() {}
        HLD(int n)
        {
            init(n);
        }
        void init(int n)
        {
            this->n = n;
            siz.resize(n);
            top.resize(n);
            dep.resize(n);
            parent.resize(n);
            dfn.resize(n);
            enddfn.resize(n);
            rk.resize(n);
            cur = 0;
            adj.assign(n, {});
        }
        void add_edges(int u, int v)
        {
            adj[u].push_back(v);
            adj[v].push_back(u);
        }
        /*
         * @brief 重链剖分（jiangly），只能剖一次，不支持动态树，节点编号和树剖编号都是从0开始。
         * @param root 根节点
         * @note 重链剖分前需要先调用init函数,调用重链剖分后，邻接表vector中存储的是重链剖分后的树，没有指向父节点的边
         * @note 重链剖分后，dfn数组中存储的是节点的dfs序，rk数组中存储的是dfs序对应的节点，enddfn数组中存储的是节点所对应子树的dfs序的结束位置的后一个（左闭右开）。
         */
        void work(int root = 0)
        {
            top[root] = root;
            dep[root] = 0;
            parent[root] = -1;
            dfs1(root);
            dfs2(root);
        }
        void dfs1(int u)
        {
            if (parent[u] != -1)
            {
                adj[u].erase(std::find(adj[u].begin(), adj[u].end(), parent[u]));
            }
            siz[u] = 1;
            for (auto &v : adj[u])
            {
                parent[v] = u;
                dep[v] = dep[u] + 1;
                dfs1(v);
                siz[u] += siz[v];
                if (siz[v] > siz[adj[u][0]])
                {
                    std::swap(v, adj[u][0]);
                }
            }
        }
        void dfs2(int u)
        {
            dfn[u] = cur++;
            rk[dfn[u]] = u;
            for (auto v : adj[u])
            {
                top[v] = v == adj[u][0] ? top[u] : v;
                dfs2(v);
            }
            enddfn[u] = cur;
        }
        /*
         * @brief 返回u到v的最近公共祖先
         * @param u 起点
         * @param v 终点
         * @return 返回u到v的最近公共祖先节点
         */
        int lca(int u, int v)
        {
            while (top[u] != top[v])
            {
                if (dep[top[u]] > dep[top[v]])
                {
                    u = parent[top[u]];
                }
                else
                {
                    v = parent[top[v]];
                }
            }
            return dep[u] < dep[v] ? u : v;
        }
        /*
         * @brief 返回u到v的距离
         * @param u 起点
         * @param v 终点
         * @return 返回u到v的距离
         */
        int dist(int u, int v)
        {
            return dep[u] + dep[v] - 2 * dep[lca(u, v)];
        }
        /*
         * @brief 跳跃
         * @param u 起点
         * @param k 跳跃距离
         * @return 返回跳跃后的节点
         */
        int jump(int u, int k)
        {
            if (dep[u] < k)
            {
                return -1;
            }

            int d = dep[u] - k;

            while (dep[top[u]] > d)
            {
                u = parent[top[u]];
            }

            return rk[dfn[u] - dep[u] + d];
        }
        /*
         * @brief 判断u是否是v的祖先
         * @param u 起点
         * @param v 终点
         * @return 返回u是否是v的祖先
         */
        bool isAncester(int u, int v)
        {
            return dfn[u] <= dfn[v] && dfn[v] < enddfn[u];
        }
        /*
        int rootedParent(int u, int v)
        {
            std::swap(u, v);
            if (u == v)
            {
                return u;
            }
            if (!isAncester(u, v))
            {
                return parent[u];
            }
            auto it = std::upper_bound(adj[u].begin(), adj[u].end(), v, [&](int x, int y)
                                       { return dfn[x] < dfn[y]; }) -
                      1;
            return *it;
        }
        int rootedSize(int u, int v)
        {
            if (u == v)
            {
                return n;
            }
            if (!isAncester(v, u))
            {
                return siz[v];
            }
            return n - siz[rootedParent(u, v)];
        }

        int rootedLca(int a, int b, int c)
        {
            return lca(a, b) ^ lca(b, c) ^ lca(c, a);
        }*/
    };

5.3 树的直径

树形 $dp$ ，求出每个点的最长路和次长路。

void dfs(int u,int fa){
    int sum1=0,sum2=0;
    f[u]=1;
    for(auto i:edge[u]){
        if(i!=fa){
            dfs(i,u);
            if(f[i]>sum1)sum2=sum1,sum1=f[i];
            else if(f[i]>sum2)sum2=f[i];
        }
    }
    if(f[u]+sum1+sum2>ans)ans=f[u]+sum1+sum2;
    f[u]+=sum1;
}

5.4 树的重心

无根树的重心点定义为树种的点 $u$ ，使得 $u$ 相邻的所有子树的子树大小均不大于树大小的一半。显然一棵树最多只有两个重心（当树节点为奇数时），且两个重心必定相邻。根据这个可以进行一定的二分（2024南京站G）

性质1

某个点是树的重心等价于它最大子树大小不大于整棵树大小的一半。

性质2

树至多有两个重心。如果树有两个重心，那么它们相邻。此时树一定有偶数个节点，且可以被划分为两个大小相等的分支，每个分支各自包含一个重心。

性质3

树中所有点到某个点的距离和中，到重心的距离和是最小的；如果有两个重心，那么到它们的距离和一样。反过来，距离和最小的点一定是重心。

性质4

往树上增加或减少一个叶子，如果原节点数是奇数，那么重心可能增加一个，原重心仍是重心；如果原节点数是偶数，重心可能减少一个，另一个重心仍是重心

性质5

把两棵树通过一条边相连得到一棵新的树，则新的重心在较大的一棵树一侧的连接点与原重心之间的简单路径上。如果两棵树大小一样，则重心就是两个连接点。

int n, sz[MAXN], mss[MAXN]; // n：总结点数（请从外部传入），sz：树的大小，mss：最大子树大小
vector<int> ctr; // 重心
void dfs(int p, int fa = 0) // 找重心
{
    sz[p] = 1, mss[p] = 0;
    for (auto [to, w] : edges[p])
        if (to != fa)
        {
            dfs(to, p);
            mss[p] = max(mss[p], sz[to]);
            sz[p] += sz[to];
        }
    mss[p] = max(mss[p], n - sz[p]);
    if (mss[p] <= n / 2) ctr.push_back(p);
}

5.5 树上差分

见数据结构静态树部分。

5.6 树上启发式合并

树上启发式合并是一种暴力的 $Trick$ ，通过小子树信息向大子树合并，实现和并查集按秩合并一样的亚线性复杂度。估算按照 $nlogn$ 算就行，也是一种乱搞做法。

示例1: 2024杭电多校1 树

给一棵根为 $1$ 的有根树，点 $i$ 具有一个权值 $A_i$ 。

定义一个点对的值 $f(u,v)=max(A_u,A_v)×|A_u−A_v|$ 。

你需要对于每个节点 $i$ ，计算 $ans_i=∑_{u∈subtree(i),v∈subtree(i)}f(u,v) $，其中 $subtree(i)$ 表示 $i$ 的子树。

请你输出 $⊕(ans_i\ mod\ 2^{64})$ ，其中 ⊕ 表示 $XOR$ .

显然硬按着结点不好想。

考虑两个子树合并， $ans_i$ 的信息是一定要继承 $ans_{u},u\in son(i)$ 的。考虑不同属于两个子树的点如何处理。

权值树合并，权值树区间合并的时候，一定是左部分的区间点权小于右部分的区间点权。所以两部分合并的时候右半区间的每一个点会额外产生

$\large\sum -sum_{lsons}\times val_{r_i}+cnt_{lson}\times val_{r_i}^2$

线段树结点维护区间 $sum$ 、区间数个数、区间 $sum^2$ 即可。然后 $nlogn$ 线段树树上启发式合并即可。

示例2：2024杭电多校3 旅行

有一棵 $n$ 个结点的无根树，每个结点都有对应的类型 $c_i$ 和权重 $w_i$ ，你需要在这棵树上规划若干次旅行。

对于一次旅行，你将从一个树上的一个结点出发，沿着树上的边进行旅行，最终到达另一个和起点类型相同的结点。

你会进行很多次旅行，但你希望对于每个结点，在所有旅行路线中最多只会经过一次。

一次旅行的价值是起始点和终止点的权重和，你需要规划旅行的方案使得旅行的总权重和最大。

$\sum n\le 2e5,c_i\le n,w_i \le 1e6$

和子树有关，考虑子树合并。

一个子树内最优解为 $dp_u$ ，那么其和另一个子树 $dp_v$ 进行合并更新。那么有两种更新方式：

$\large dp_u=max(dp_u+dp_v,\{f_{u,c}+f_{v,c}\})$

其中 $f_{u,c}$ 表示 $u$ 子树上传一个颜色为 $c$ 的路径接口所能提供的最大权值和。显然 $dp_u$ 是不提供上传路径的。

对 $f_{u,c}$ 的更新有下列式子，出于启发式合并，如果 $v$ 上传路径穿过 $u$ ，则不能使用 $dp_u$

$f_{u,c}=max(f_{u,c}+dp_v,f_{v,c}+\sum_{t\in son(u)} dp_t)$

启发式线段树合并即可。

#pragma GCC optimize(3, "Ofast", "inline")
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
const i64 mod = 998244353;
#define endl '\n'
#define int long long
struct node
{
    int l, r;
    i64 f;
    i64 lz = 0;
};
const int maxn = 3e5 + 9;
node tree[maxn << 5];
int tot = 0;
int newnode()
{
    tot++;
    tree[tot] = {0, 0, 0, 0};
    return tot;
}
void pushup(int rt)
{
    tree[rt].f = max(tree[tree[rt].l].f, tree[tree[rt].r].f);
    return;
}
void pushd(int rt)
{
    if (tree[rt].lz)
    {
        if (tree[rt].l)
        {
            tree[tree[rt].l].f += tree[rt].lz;
            tree[tree[rt].l].lz += tree[rt].lz;
        }
        if (tree[rt].r)
        {
            tree[tree[rt].r].f += tree[rt].lz;
            tree[tree[rt].r].lz += tree[rt].lz;
        }
        tree[rt].lz = 0;
    }
    return;
}
void upd(int &rt, int pos, int val, int cl, int cr)
{
    if (!rt)
        rt = newnode();
    if (cl == cr)
    {
        tree[rt].f = val;
        return;
    }
    pushd(rt);
    int mid = (cl + cr) >> 1;
    if (pos <= mid)
        upd(tree[rt].l, pos, val, cl, mid);
    else
        upd(tree[rt].r, pos, val, mid + 1, cr);
    pushup(rt);
    return;
}
vector<i64> dp, dpson, w, c;
int n;
vector<vector<int>> con;
vector<int> root;
void merges(int &rt1, int &rt2, int cl, int cr, i64 &ans, i64 dpv, i64 dpson)
{
    if (!rt1 || !rt2)
    {
        if (rt1)
        {
            tree[rt1].f += dpv;
            tree[rt1].lz += dpv;
        }
        else
        {
            tree[rt2].f += dpson;
            tree[rt2].lz += dpson;
        }
        rt1 |= rt2;
        return;
    }
    if (cl == cr)
    {
        ans = max(ans, tree[rt1].f + tree[rt2].f);
        tree[rt1].f = max(tree[rt1].f + dpv, tree[rt2].f + dpson);
        return;
    }
    int mid = (cl + cr) >> 1;
    pushd(rt1), pushd(rt2);
    merges(tree[rt1].l, tree[rt2].l, cl, mid, ans, dpv, dpson);
    merges(tree[rt1].r, tree[rt2].r, mid + 1, cr, ans, dpv, dpson);
    pushup(rt1);
    return;
}
void dfs(int u, int f)
{
    upd(root[u], c[u], w[u], 1, n);
    dp[u] = 0, dpson[u] = 0;
    for (auto &v : con[u])
    {
        if (v == f)
            continue;
        dfs(v, u);
        i64 tmp = 0;
        merges(root[u], root[v], 1, n, tmp, dp[v], dpson[u]);
        dp[u] = max(dp[u] + dp[v], tmp);
        dpson[u] += dp[v];
    }
}
void solve()
{
    tot = 0;
    cin >> n;
    dp.assign(n + 1, 0);
    dpson.assign(n + 1, 0);
    w.assign(n + 1, 0);
    c.assign(n + 1, 0);
    root.assign(n + 1, 0);
    for (int i = 1; i <= n; i++)
        cin >> c[i];
    for (int i = 1; i <= n; i++)
        cin >> w[i];
    con.assign(n + 1, vector<int>());
    for (int i = 1; i < n; i++)
    {
        int u, v;
        cin >> u >> v;
        con[u].push_back(v);
        con[v].push_back(u);
    }
    dfs(1, 0);
    cout << dp[1] << endl;
}

signed main()
{
    // freopen("1002.in", "r", stdin);
    // freopen("1.out", "w", stdout);
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--)
        solve();
}

示例3：（未知来源，朱的例题）

//处理子树相关的问题，不支持修改，nlogn的复杂度，离线算法
#include<bits/stdc++.h>
#define LL long long 
using namespace std;
const int MAXN = 1e5 + 10;
inline int read() {
    char c = getchar(); int x = 0, f = 1;
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar();
    return x * f;
}
int N, col[MAXN], son[MAXN], siz[MAXN], cnt[MAXN], Mx, Son;
LL sum = 0, ans[MAXN];
vector<int> v[MAXN];
void dfs(int x, int fa) {
    siz[x] = 1;
    for(int i = 0; i < v[x].size(); i++) {
        int to = v[x][i];
        if(to == fa) continue;
        dfs(to, x);
        siz[x] += siz[to];
        if(siz[to] > siz[son[x]]) son[x] = to;//轻重链剖分
    }
}
void add(int x, int fa,int c) {//暴力计算x的子树颜色和，不考虑重边，
    cnt[col[x]] +=c;//这里可能会因题目而异
    if(cnt[col[x]] > Mx) Mx = cnt[col[x]], sum = col[x];
    else if(cnt[col[x]] == Mx) sum += (LL)col[x];
    for(int i = 0; i < v[x].size(); i++) {
        int to = v[x][i];
        if(to == fa || to == Son) continue;
        add(to, x,c);
    }
}
void dfs2(int x, int fa, int opt) {//处理当前节点的答案
    for(int i = 0; i < v[x].size(); i++) {
        int to = v[x][i];
        if(to == fa) continue;
        if(to != son[x]) dfs2(to, x, 0);//简单的往轻边走算轻边的答案，opt = 0表示递归完成后消除对该点的影响
    }
    if(son[x]) dfs2(son[x], x, 1), Son = son[x];//统计重儿子的贡献，不消除影响
    //这时候的sum和Mx都是只考虑重儿子计算出来的
    add(x, fa,1); Son = 0;
    //暴力统计所有轻儿子的贡献，会递归所有轻儿子，除了当前节点的重儿子，而不是son[x]，因为轻儿子的重儿子是需要计算的，这里只是不需要计算x的重儿子
    ans[x] = sum;//更新答案
    if(!opt) add(x,fa,-1), sum = 0, Mx = 0;//如果需要删除贡献的话就删掉
}
int main() {
    N = read();
    for(int i = 1; i <= N; i++) col[i] = read();
    for(int i = 1; i <= N - 1; i++) {
        int x = read(), y = read();
        v[x].push_back(y); v[y].push_back(x);
    }
    dfs(1, 0);
    dfs2(1, 0, 1);
    for(int i = 1; i <= N; i++) printf("%I64d ", ans[i]);
    return 0;
}

6.图的连通性

6.1 无向图连通性

无向图的连通性主要关于点双联通分量和边双联通分量，用于操作缩点以及缩边，从而把无向图中的环删掉。

6.1.1 割点

对于一个无向图，如果把一个点删除后这个图的极大连通分量数增加了，那么这个点就是这个图的割点（又称割顶）。

#include<bits/stdc++.h>
#define pb push_back
using namespace std;
const int N=2e4+1e3;
int n,m,ans;
vector<int> g[N];
bool cut[N];
int dfn[N],low[N],cnt;
void tarjan(int u,int root){
    dfn[u]=low[u]=++cnt;
    int child=0;
    for(auto v:g[u]){
        if(!dfn[v]){
            tarjan(v,root),low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u]&&u!=root) cut[u]=true;//如果儿子的low值大于等于dfn，则代表其为儿子与其他非子树点相连的唯一途径
            if(u==root) child++;
        }
        else low[u]=min(low[u],dfn[v]);//注意这里是dfn[v]
    //因为割点判定法则是小于等于号，所以在求割点时，不必考虑父节点和重边的问题，从x出发能访问到的所有点的时间戳都可以用来更新 lowx
    }
    if(child>=2&&u==root)cut[u]=true;//对根的处理,大于两个子树
}
int main(){
    cin>>n>>m;
    for(int i=1,u,v;i<=m;i++){
        cin>>u>>v;
        g[u].pb(v);g[v].pb(u);
    }
    for(int i=1;i<=n;i++)
        if(!dfn[i]) tarjan(i,i);
    for(int i=1;i<=n;i++)
        if(cut[i]) ans++;
    cout<<ans<<endl;
    for(int i=1;i<=n;i++)
        if(cut[i]) cout<<i<<" ";
    return 0;
}

6.1.2 割边

对于一个无向图，如果删掉一条边后图中的连通分量数增加了，则称这条边为桥或者割边。严谨来说，就是：假设有连通图 $G=(V,E)$ ， $e$ 是其中一条边（即 $e\in E$ )，如果 $G-e$ 是不连通的，则边 $e$ 是图 $G$ 的一条割边（桥)。

#include<bits/stdc++.h>
#define pb push_back
using namespace std;
const int N=200;
int n,m,sum;
int a[200][200];
bool cut[N];
int dfn[N],low[N],cnt,fa[N];
struct Edge {
    int x,y;
} edge[5001];
bool cmp(struct Edge a,struct Edge b) {
    if(a.x==b.x)return a.y<b.y;
    return a.x<b.x;
}
void tarjan(int u){
    dfn[u]=low[u]=++cnt;
    for(int v=1; v<=n; v++) {
        if(!a[u][v])continue;
        if(!dfn[v]){
            fa[v]=u,tarjan(v),low[u]=min(low[u],low[v]);
            if(low[v]>dfn[u]) edge[++sum].x=u, edge[sum].y=v;//儿子回不到父亲以上的位置
        }
        else if(v!=fa[u])low[u]=min(low[u],dfn[v]);//注意这里不能是fa[u],不然上面的if那里一定取不了大于号！
        //low的意思这里是不经过父亲能回到的最早的点
    }
}
int main(){
    cin>>n>>m;
    for(int i=1,u,v;i<=m;i++){
        cin>>u>>v;
        a[u][v]=a[v][u]=1;
    }
    for(int i=1; i<=n; i++) 
        if(!dfn[i])tarjan(i);//tarjan
    sort(edge+1,edge+sum+1,cmp);
    for(int i=1;i<=sum; i++) {
        cout<<min(edge[i].x,edge[i].y)<<' '<<max(edge[i].x,edge[i].y)<<endl;//输出
    }
    return 0;
}

封装风格：

map<array<int, 3>, int> mp;
    vector<int> dfn(n), low(n), fa(n);
    int cnt = 0;
    function<void(int)> tarjan = [&](int u)
    {
        dfn[u] = low[u] = ++cnt;
        for (auto [v, w] : newcon[u])
        {
            if (!dfn[v])
            {
                fa[v] = u, tarjan(v), low[u] = min(low[u], low[v]);
                if (low[v] > dfn[u])
                    mp[{u, v, w}] = mp[{v, u, w}] = 1; // 割边
            }
            else if (v != fa[u])
                low[u] = min(low[u], dfn[v]);
        }
    };
    for (int i = 0; i < n; i++)
        if (!dfn[i])
            tarjan(i);

6.1.3 点双

若一个无向图中的去掉任意一个点都不会改变此图的连通性，即不存在割点，则称作点双连通图。一个无向图中的每一个极大点双连通子图称作此无向图的点双连通分量。

对于两个点 $u,v$ ，如果删除除他们自己外哪一个点都不能使其不联通，则称两点之间双联通。点双联通不具有传递性。

/*点双连通：若对于一个无向图，其任意一个节点对于这个图本身而言都不是割点，则称其点双连通。也就是说，删除任意点及其相关边后，整个图仍然属于一个连通分量。

点双连通分量：无向图中，极大的点双连通子图。与连通分量类似，抽离出一些点及它们之间的边，使得抽离出的图是一个点双连通图，在这个前提下，使得抽离出的图越大越好。*/

/*桥（割边）不属于任何 e-DCC（边双连通分量），但是割点可能属于多个 v-DCC*/
#include <iostream>
#include <vector>
using namespace std;
const int N = 1000010, M = 5000010;
int dfn[N], low[N], stack[N],cut[N];
int n, m, tot = 1, num, root, top, sum, cnt;
vector<int> dcc[N * 2];//dcc[i] 存储编号为 i 的 v-DCC 中的所有节点
vector<int> edge[N];
void tarjan(int u,int root) {
    //不用特别根节点是不是割点，它一定属于它儿子的点双中，无论是不是割点
    dfn[u] = low[u] = ++cnt;
    stack[++top] = u;
    if (u == root && edge[u].size() == 0) { //孤立点直接处理
        dcc[++sum].push_back(u);
        return;
    }
    for (auto v:edge[u]) {
        if (!dfn[v]) {
            tarjan(v,root);low[u] = min(low[u], low[v]);
            if (low[v] >= dfn[u]) {//u为割点，把栈里u前的都要出去
                sum++;
                int z;
                do {//弹栈
                    z = stack[top--];
                    dcc[sum].push_back(z);
                } while (z != v);//把v弹走后目前栈顶为u(u为割点)，u不能弹走因为它属于多个点双（至少2）
                dcc[sum].push_back(u);//单独加入u
            }
        } 
        else low[u] = min(low[u], dfn[v]);
    }
}
int main() {
    ios::sync_with_stdio(false);
    cin>>n>>m;
    for(int i=1,u,v;i<=m;i++){
        cin>>u>>v;
        if(u!=v)edge[u].push_back(v),edge[v].push_back(u);//判自环
    }
    for (int i=1;i<=n;i++)
        if (!dfn[i])tarjan(i,i);
    //for (int i=1;i<=n;i++)cout<<low[i]<<endl;
    cout<<sum<<endl;
    for (int i=1;i<=sum;i++) { 
        cout<<dcc[i].size();
        for (auto j:dcc[i])
            cout << ' ' << j;
        cout<<endl;
    }

6.1.4 边双

若一个无向图中的去掉任意一条边都不会改变此图的连通性，即不存在割桥，则称作边双连通图。一个无向图中的每一个极大边双连通子图称作此无向图的边双连通分量。

在一张连通的无向图中，对于两个点 $u$ 和 $v$ ，如果无论删去哪条边（只能删去一条）都不能使它们不连通，我们就说 $u$ 和 $v$ 边双连通。边双联通具有传递性

//边双连通分量，很显然，边双连通分量中没有割边，所以只需要去掉所有桥边剩下的就是边双，跑dfs即可
//注意这里可能有重边，所以我们存图的时候额外存一下每边的数量（map），找桥的时候正常找，如果非桥边有多个不影响，桥边有多个就说明额外连起来了两个v-ecc，所以我们找到桥边就数量-1，dfs的时候正常dfs，如果桥边还有那就走，没有的话就说明是一个v-ecc
//用于无向图的缩点
#include<bits/stdc++.h>
#define pb push_back
using namespace std;
const int N=5e5+10;
int n,m,sum;
int dfn[N],low[N],cnt,fa[N],vis[N];
unordered_map<int,int>mp[N];
vector<int>edge[N],ans[N];//ans即是bcc
void tarjan(int u){
    dfn[u]=low[u]=++cnt;
    for(auto v:edge[u]) {
        if(!dfn[v]){
            fa[v]=u,tarjan(v),low[u]=min(low[u],low[v]);
            if(low[v]>dfn[u]) mp[u][v]--,mp[v][u]--;//儿子回不到父亲以上的位置
        }
        else if(v!=fa[u])low[u]=min(low[u],dfn[v]);//注意这里不能是fa[u],不然上面的if那里一定取不了大于号！
        //low的意思这里是不经过父亲能回到的最早的点
    }
}
void dfs(int u,int k){
    ans[k].emplace_back(u);
    vis[u]=1;
    for(auto v:edge[u]){
        if(!vis[v]&&mp[u][v]){
            dfs(v,k);
        }
    }
}
int main(){
    cin>>n>>m;
    for(int i=1,u,v;i<=m;i++){
        cin>>u>>v;
        if(u==v)continue;
        if(mp[u].find(v)==mp[u].end()||mp[v].find(u)==mp[v].end()){
            edge[u].push_back(v);
            edge[v].push_back(u);
            mp[u][v]=1;
            mp[v][u]=1;
        }
        else  mp[u][v]++,mp[v][u]++;
    }
    for(int i=1; i<=n; i++) 
        if(!dfn[i])tarjan(i);//tarjan
    for(int i=1; i<=n; i++) {
        if(!vis[i]){
            sum++;
            dfs(i,sum);
        }
    }
    cout<<sum<<endl;
    for(int i=1;i<=sum;i++){
        cout<<ans[i].size()<<" ";
        for(auto j:ans[i])cout<<j<<" ";
        cout<<endl;
    }
    return 0;
}

*6.1.5 圆方树

//点双的关键性质:对于一个点双中的两点，它们之间简单路径的并集，恰好完全等于这个点双。
//即同一个点双中的两不同点 u,v 之间一定存在一条简单路径经过给定的在同一个点双内的另一点 w。所以看到简单路径的时候，可以考虑圆方树
//圆方树：点双当作一个点，这个点和所有点连边形成的树，这样不同点双会靠割点联系起来形成一棵树
#include<bits/stdc++.h>
#define int long long
#define endl '\n'//交互题就删
using namespace std;
const int N = 100005;
int n,m, cnt;
int dfn[N], low[N], dfc;
int stk[N], tp;
vector<int> G[N], T[N * 2];//相关数组开两倍！！！
void tarjan(int u) {
    low[u] = dfn[u] = ++dfc; //dfs序
    stk[++tp] = u; 
    for (auto v : G[u]) { // 遍历 u 的相邻节点
        if (!dfn[v]) { 
            tarjan(v); low[u] = min(low[u], low[v]); 
            if (low[v] == dfn[u]) { // 找到一个以 u 为根的点双连通分量
                ++cnt; // 增加方点个数
                for (int x = 0; x != v; --tp) {// 将点双中除了 u 的点退栈，并在圆方树中连边
                    x = stk[tp];
                    T[cnt].push_back(x);
                    T[x].push_back(cnt);
                }
                T[cnt].push_back(u);
                T[u].push_back(cnt);
            }
        }
        else low[u] = min(low[u], dfn[v]); // 已访问的和 dfn 取 min
    }
}
signed main() {
    cin>>n>>m;
    cnt = n; 
    for (int i = 1; i <= m; ++i) {
        int u, v;cin>>u>>v;
        G[u].push_back(v); 
        G[v].push_back(u);
    }
    // 处理非连通图
    for (int u = 1; u <= n; ++u)
        if (!dfn[u]) tarjan(u), --tp;
        // 注意到退出 Tarjan 时栈中还有一个元素即根，将其退栈
    return 0;
}

6.2 有向图连通性

6.2.1 强连通分量

强连通的定义是：有向图 G 强连通是指，G 中任意两个结点连通。

强连通分量（Strongly Connected Components，SCC）的定义是：极大的强连通子图

#include <bits/stdc++.h> //O(n+m)
#define int long long
#define endl '\n'
using namespace std;
const int inf = 0x3f3f3f3f;
const int N = 1e5 + 10;
const int M = 1e6 + 10;
int n, m, u, v, cnt, sum;
int dfn[N], low[N], vis[N], belong[N], flag[N]; // belong的含义是这个点是否属于一个强连通分量，low[x] x能通过有向边能回溯到的最早时间段
vector<int> edge[N];
vector<int> q[N];
stack<int> s;
void tarjan(int x)
{ // tarjan算法，处理x所在的连通块的强连通分量
    dfn[x] = low[x] = ++cnt;
    vis[x] = 1;
    s.push(x);
    for (auto i : edge[x])
    {
        if (!dfn[i])
            tarjan(i), low[x] = min(low[i], low[x]);
        else if (!belong[i])
            low[x] = min(dfn[i], low[x]);
        // 如果这个点不属于任何一个强连通分量，说明在栈中，即需要考虑更新low值
        // 不在栈里说明不可能存在于一个强连通分量(访问过了又不在栈里，说明已经是一个强连通分量出去了)
    }
    if (low[x] == dfn[x])
    { // 回溯时把（x到栈顶的点）全归为一个强连通分量
        ++sum;
        q[sum].push_back(x);
        vis[x] = 0; // 退栈
        belong[x] = sum;
        while (s.top() != x)
        {
            int t = s.top();
            s.pop();
            q[sum].push_back(t);
            belong[t] = sum;
            vis[t] = 0;
        }
        s.pop();
    }
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
    {
        cin >> u >> v;
        edge[u].push_back(v);
    }
    for (int i = 1; i <= n; i++)
        if (!dfn[i])
            tarjan(i);
    cout << sum << endl;
    for (int i = 1; i <= n; i++)
    {
        if (!flag[i])
        {
            sort(q[belong[i]].begin(), q[belong[i]].end());
            for (auto j : q[belong[i]])
            {
                flag[j] = 1;
                cout << j << " ";
            }
            cout << endl;
        }
    }
}

6.2.2 缩点

缩点的本质就是一个环可以等效处理成一个点时，我们把旧图的每一个强连通分量当作一个点建立一个新图，并把一个环的信息全部统计到一个新点上。

给定一个 $n$ 个点 $m$ 条边有向图，每个点有一个权值，求一条路径，使路径经过的点权值之和最大。你只需要求出这个权值和。

允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。

#include <bits/stdc++.h> //缩点的本质就是一个环可以等效处理成一个点时，我们把旧图的每一个强连通分量当作一个点建立一个新图，并把一个环的信息全部统计到一个新点上
#define int long long
#define endl '\n'
using namespace std;
const int inf = 0x3f3f3f3f;
const int N = 1e5 + 10;
const int M = 1e6 + 10;
int n, m, u, v, cnt, sum, k;
int dfn[N], low[N], vis[N], belong[N], a[N], b[N], in[N], c[N], f[N];
vector<int> edge[N];
vector<int> out[N];
vector<int> inn[N];
vector<int> q[N];
stack<int> s;
void topo()
{
    queue<int> q;
    for (int i = 1; i <= sum; i++)
        if (!in[i])
            q.push(i);
    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        c[++k] = u;
        for (auto j : out[u])
        {
            in[j]--;
            if (!in[j])
                q.push(j);
        }
    }
}
void tarjan(int x)
{ // tarjan算法
    dfn[x] = low[x] = ++cnt;
    vis[x] = 1;
    s.push(x);
    for (auto i : edge[x])
    {
        if (!dfn[i])
            tarjan(i), low[x] = min(low[i], low[x]);
        else if (vis[i])
            low[x] = min(low[i], low[x]);
    }
    if (low[x] == dfn[x])
    {
        ++sum;
        q[sum].push_back(x);
        vis[x] = 0;
        belong[x] = sum;
        while (s.top() != x)
        {
            int t = s.top();
            s.pop();
            q[sum].push_back(t);
            belong[t] = sum;
            vis[t] = 0;
        }
        s.pop();
    }
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    for (int i = 1; i <= m; i++)
    {
        cin >> u >> v;
        edge[u].push_back(v);
    }
    for (int i = 1; i <= n; i++)
        if (!dfn[i])
            tarjan(i);
    // 现在有sum个强连通分量，接下来将每个强连通分量的信息统计到一个点上
    for (int i = 1; i <= sum; i++)
    {
        for (auto j : q[i])
        {
            b[i] += a[j];
        }
    }
    // b数组储存了每个强连通分量的权值和，统计完毕后建立新图
    // 建图时注意考虑，两个强连通分量之间可能会有多重边！！搜索时注意vis数组
    for (int i = 1; i <= n; i++)
    {
        for (auto j : edge[i])
        {
            if (belong[i] == belong[j])
                continue;
            out[belong[i]].push_back(belong[j]);
            inn[belong[j]].push_back(belong[i]);
            in[belong[j]]++;
        }
    }
    topo();
    // 拓扑排序来决定dp转移顺序，因为一个点的最优解是从它的所有来边转移过来的，拓扑排序决定了在处理当前点时，它的来边已经全部处理好了
    for (int i = 1; i <= k; i++)
    {
        int u = c[i];
        f[u] = b[u];
        for (auto j : inn[u])
        { // 直接转移就可以
            f[u] = max(f[u], f[j] + b[u]);
        }
    }
    int ans = 0;
    for (int i = 1; i <= k; i++)
        ans = max(ans, f[i]);
    cout << ans;
}

*6.2.3 2-SAT适定性问题

有 $n$ 个布尔变量 $x_1$ $\sim$ $x_n$ ，另有 $m$ 个需要满足的条件，每个条件的形式都是「 $x_i$ 为 true / false 或 $x_j$ 为 true / false」。比如「 $x_1$ 为真或 $x_3$ 为假」、「 $x_7$ 为假或 $x_2$ 为假」。

2-SAT 问题的目标是给每个变量赋值使得所有条件得到满足。

输入格式

第一行两个整数 $n$ 和 $m$ ，意义如题面所述。

接下来 $m$ 行每行 $4$ 个整数 $i$ , $a$ , $j$ , $b$ ，表示「 $x_i$ 为 $a$ 或 $x_j$ 为 $b$ 」( $a, b\in \{0,1\}$ )

输出格式

如无解，输出 IMPOSSIBLE；否则输出 POSSIBLE。

下一行 $n$ 个整数 $x_1\sim x_n$ （ $x_i\in\{0,1\}$ ），表示构造出的解。

$1\leq n, m\leq 10^6$

/*实际的问题里往往是给出一个更细致的情景，而且题干信息中
会有二选一的标志，此时可以考虑往2-sat模型上考虑。考虑过程，即
去寻找题目中的限制，把二选一等信息，转化为一个蕴含关系，即
a ⇒ b 这样的式子*/
// 其中一个不成立则另一个一定成立
#include <bits/stdc++.h> //O(n+m)
#define int long long
#define endl '\n'
using namespace std;
const int inf = 0x3f3f3f3f;
const int N = 2e6 + 10;
const int M = 2e6 + 10;
int n, m, u, v, cnt, sum;
int dfn[N], low[N], vis[N], belong[N], flag[N]; // belong的含义是这个点是否属于一个强连通分量，low[x] x能通过有向边能回溯到的最早时间段
vector<int> edge[N];
vector<int> q[N];
stack<int> s;
void tarjan(int x)
{ // tarjan算法，处理x所在的连通块的强连通分量
    dfn[x] = low[x] = ++cnt;
    vis[x] = 1;
    s.push(x);
    for (auto i : edge[x])
    {
        if (!dfn[i])
            tarjan(i), low[x] = min(low[i], low[x]);
        else if (!belong[i])
            low[x] = min(dfn[i], low[x]);
        // 如果这个点不属于任何一个强连通分量，说明在栈中，即需要考虑更新low值
        // 不在栈里说明不可能存在于一个强连通分量(访问过了又不在栈里，说明已经是一个强连通分量出去了)
    }
    if (low[x] == dfn[x])
    { // 回溯时把（x到栈顶的点）全归为一个强连通分量
        ++sum;
        q[sum].push_back(x);
        vis[x] = 0; // 退栈
        belong[x] = sum;
        while (s.top() != x)
        {
            int t = s.top();
            s.pop();
            q[sum].push_back(t);
            belong[t] = sum;
            vis[t] = 0;
        }
        s.pop();
    }
}
void add(int a, int b)
{
    edge[a].push_back(b);
}
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
    {
        int a, b, x, y;
        cin >> a >> x; // 第a个数为x或第b个数为y
        cin >> b >> y;
        if (x == 0 && y == 0) //"如果第a个数为0或第b个数为0"至少满足其一
        {
            add(a + n, b); // a=1则b=0
            add(b + n, a); // b=1则a=0
        }
        if (x == 0 && y == 1) //"如果第a个数为0或第b个数为1"至少满足其一
        {
            add(a + n, b + n); // a=1则b=1
            add(b, a);         // b=0则a=0
        }
        if (x == 1 && y == 0) //"如果第a个数为1或第b个数为0"至少满足其一
        {
            add(a, b);         // a=0则b=0
            add(b + n, a + n); // b=1则a=1
        }
        if (x == 1 && y == 1) //"如果第a个数为1或第b个数为1"至少满足其一
        {
            add(a, b + n); // a=0则b=1
            add(b, a + n); // b=0则a=1
        }
    }
    for (int i = 1; i <= 2 * n; i++)
        if (!dfn[i])
            tarjan(i); // 两倍
    for (int i = 1; i <= n; i++)
    {
        if (belong[i] == belong[i + n]) // 同一变量的两种取值在同一强联通分量里,说明无解
        {
            cout << "IMPOSSIBLE" << endl;
            return 0;
        }
    }
    cout << "POSSIBLE" << endl; // 否则就是有解
    for (int i = 1; i <= n; i++)
    {
        if (belong[i] > belong[i + n])
            cout << 1 << " "; // 两种取值中选择拓扑序较大的那个值，而强联通分量编号越小 -> 拓扑序越大 -> 越优
        else
            cout << 0 << " ";
    }
    return 0;
}

*7. 基环树

基环树，只有一个环的树，边数为 $n$ .

//1. 暴力删边
//每次断开环上的一条边跑一遍答案，然后取最大值  适用于:数据较小，且环不会影响答案的题目
//eg：旅行，每次的旅行一定是走n-1条边，直接暴力枚举删掉某一条边，跑一次答案 ，n^2过
#include<bits/stdc++.h>
#define int long long
#define endl '\n'//交互题就删
using namespace std;
const int inf=0x3f3f3f3f;
const int N=2e5+10;
int n,m,x[N],y[N],ans[N],cnt,tx,ty,sum[N],vis[N];
vector<int>edge[N];
void dfs(int u,int fa){
    ans[++cnt]=u;
    for(auto i:edge[u]){
        if(i!=fa){
            dfs(i,u);
        }
    }
}
void dfs2(int u,int fa){
    vis[u]=1;
    sum[++cnt]=u;
    for(auto i:edge[u]){
        if(i!=fa){
            if((i==tx&&u==ty)||(i==ty&&u==tx)||vis[i])continue;
            dfs2(i,u);
        }
    }
}
bool check(){
    for(int i=1;i<=n;i++){
        if(sum[i]==ans[i])continue;
        else if(sum[i]>ans[i])return 0;
        else return 1;
    }
}
signed main(){
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    cin>>n>>m;
    for(int u,v,i=1;i<=m;i++){
        cin>>u>>v;
        edge[u].push_back(v);
        edge[v].push_back(u);
        x[i]=u;y[i]=v;
    }
    for(int i=1;i<=n;i++)
        sort(edge[i].begin(),edge[i].end());
    if(m==n-1){
        dfs(1,0);
        for(int i=1;i<=n;i++)
            cout<<ans[i]<<" ";
        return 0;
    }
    for(int i=1;i<=m;i++){
        memset(vis,0,sizeof(vis));
        tx=x[i],ty=y[i];cnt=0;
        dfs2(1,0);
        if(cnt<n)continue;
        if(ans[1]==0)
            for(int j=1;j<=n;j++)ans[j]=sum[j];
        else if(check())
            for(int j=1;j<=n;j++)ans[j]=sum[j];
    }
    for(int i=1;i<=n;i++)
        cout<<ans[i]<<" ";
    return 0;
}
//2. 断边跑两次
//骑士，每个人有个讨厌的人，那么就是n个点n条边，形成了基环树，注意到环上的某一条边，意味着u和v不能同时选，我们计算两种情况，选u和选v
//等价于强制隔开这两个人各自选一次
//正确性：每个人只有一个讨厌的人，那么最终情况一定是，要么有他，要么有他讨厌的人，不可能都没有，所以跑两次是正确的
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
#define N 1000010
const int inf=0x3f3f3f3f;
using namespace std;
int w[N],d[N],n,vis[N],flag,f[N][2],ans;
vector<int>edge[N];
void dp(int u){
    vis[u]=1;
    f[u][0]=0;f[u][1]=w[u];
    for(auto i:edge[u]){
        if(i!=flag){//不能dp回根
            dp(i);
            f[u][0]+=max(f[i][0],f[i][1]);
            f[u][1]+=f[i][0];
        }
    }
}
void dfs(int u){
    vis[u]=1;
    if(vis[d[u]])flag=u;
    else dfs(d[u]);
}
signed main(){
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    cin>>n;
    for(int u,v,i=1;i<=n;i++){
        cin>>w[i]>>d[i];
        edge[d[i]].push_back(i);//存的是仇恨他的人有哪些
    }
    for(int i=1;i<=n;i++){
        if(vis[i])continue;
        dfs(i);
        //现在已经找到了一个环上的一条边:flag 和 d[flag]
        //我们强制其中一个点不选
        dp(flag);
        int ans1=f[flag][0];//不选flag
        flag=d[flag];
        dp(flag);
        int ans2=f[flag][0];//不选d[flag]
        ans+=max(ans1,ans2);
    }
    cout<<ans<<endl;
}

Part 5. 字符串

强制规定：所有与字符串相关的数组下标或者函数接口如果未特殊说明，都是从 $0$ 开始。

1.字符串哈希（双哈希）

template <int m1, int mod1, int m2, int mod2>
struct Stringhashs
{
    int n;
    vector<i64> h1, h2, mi1, mi2;
    string s;
    void init(int n)
    {
        this->n = n;
        h1.resize(n + 10);  // h1[i]表示前i个字符的哈希值，注意哈希数组是从1开始的
        h2.resize(n + 10);  // h2[i]表示前i个字符的哈希值
        mi1.resize(n + 10); // mi1[i]表示m1^i,哈希模数
        mi2.resize(n + 10); // mi2[i]表示m2^i,哈希模数
        mi1[0] = mi2[0] = 1;
        s.clear();
        for (int i = 1; i <= n; i++)
        {
            mi1[i] = (i64)mi1[i - 1] * m1 % mod1;
            mi2[i] = (i64)mi2[i - 1] * m2 % mod2;
            h1[i] = ((i64)h1[i - 1] * m1 + s[i - 1]) % mod1;
            h2[i] = ((i64)h2[i - 1] * m2 + s[i - 1]) % mod2;
        }
    }
    void insert(string s)
    {
        assert(s.size() <= n);
        this->s = s;
        for (int i = 0; i < s.size(); i++)
        {
            h1[i + 1] = ((i64)h1[i] * m1 % mod1 + s[i]) % mod1;
            h2[i + 1] = ((i64)h2[i] * m2 % mod2 + s[i]) % mod2;
        }
    }
    array<int, 2> queryfullhash(string s)
    {
        int h1 = 0, h2 = 0;
        for (int i = 0; i < s.size(); i++)
        {
            h1 = ((i64)h1 * m1 % mod1 + s[i]) % mod1;
            h2 = ((i64)h2 * m2 % mod2 + s[i]) % mod2;
        }
        return {h1, h2};
    }
    array<int, 2> query(int l, int r)
    {
        assert(n);
        assert(l >= 0 && r < n && l <= r);
        l++, r++;
        int h1 = ((this->h1[r] - (i64)this->h1[l - 1] * mi1[r - l + 1] % mod1) % mod1 + mod1) % mod1;
        int h2 = ((this->h2[r] - (i64)this->h2[l - 1] * mi2[r - l + 1] % mod2) % mod2 + mod2) % mod2;
        return {h1, h2};
    }
};
const int mod1 = 1e9 + 7, mod2 = 998244353;
using hashs = Stringhashs<131, mod1, 13331, mod2>;

2.KMP字符串匹配

适配：文本串固定 $T$ ，多个主串 $S$ ，询问 $T$ 在 $S$ 中出现的次数。时间复杂度 $O(|T|+\sum |S|)$

2.1 前缀函数与nxt数组

前缀函数定义： $\pi[i]$ 表示 $s.substr(0,i+1)$ 中公共前后缀的长度。即有 $s[0,\cdots,\pi[i]-1]=s[i-\pi[i]+1,\cdots,i]$ 。

规定长度为 $1$ 的字符串前缀函数为 $0$ 。

vector<int> prefix_function(string s) {
  int n = (int)s.length();
  vector<int> pi(n);
  for (int i = 1; i < n; i++) {
    int j = pi[i - 1];
    while (j > 0 && s[i] != s[j]) j = pi[j - 1];
    if (s[i] == s[j]) j++;
    pi[i] = j;
  }
  return pi;
}

基于此维护的 $KMP\ nxt$ 数组就是方便寻找失配之后下一个配对的位置：

nxt[0] = 0;
        for (int i = 1, j = 0; i < T.size(); i++)
        {
            while (j && T[i] != T[j])
                j = nxt[j - 1];
            if (T[i] == T[j])
                j++;
            nxt[i] = j;
        }

2.2 KMP字符串模式匹配算法

$KMP$ 算法的精髓在于当前匹配失配之后模式串 $T$ 的指针跳到哪里开始重新匹配的问题。因为已匹配部分保证了两段相同，那么只需要跳到公共前后缀的前缀后一位继续匹配就行了。前缀函数是对模式串 $T$ 求解的。

$KMP$ 匹配思想不只局限于字符串匹配，与匹配有关的 $dp$ 题也会利用到 $nxt$ 数组的思想来优化 $dp$ 。

struct KMP
{
    string T;
    vector<int> nxt;
    KMP(string T) : T(T)
    {
        nxt.resize(T.size());
        nxt[0] = 0;
        for (int i = 1, j = 0; i < T.size(); i++)
        {
            while (j && T[i] != T[j])
                j = nxt[j - 1];
            if (T[i] == T[j])
                j++;
            nxt[i] = j;
        }
    }
    vector<int> match(string S)
    {
        vector<int> res;
        for (int i = 0, j = 0; i < S.size(); i++)
        {
            while (j && S[i] != T[j])
                j = nxt[j - 1];
            if (S[i] == T[j])
                j++;
            if (j == T.size())
            {
                res.push_back(i - j + 1);
                j = nxt[j - 1];
            }
        }
        return res;
    }
};

示例1:2024湖南省赛经文

题目大意：有一个长度为 $n\le 1000$ 的空串和长度为 $t\le 100$ 的模式串 $T$ ，询问有多少用小写英文字母填充空串的方案数，使得 $T$ 于其中不相交的出现精准 $k$ 次。

设 $dp_{i,j,l}$ 表示前 $i$ 个字符已经匹配了 $j$ 个完整文本串，现在正在匹配 $l$ 位置的方案数。枚举 $26$ 个小写字母，初始匹配指针 $pre=l$

如果 $s[pre]==char$ ，则直接有 $dp[i][j][pre+1]+=dp[i][j][l]$ ，满一个则 $j$ 进位。

如果该字符导致了 $fail$ 匹配，则类似 $KMP$ 跳转 $pre=nxt[pre-1]$ ，继续下一个位置的匹配，直到 $pre=0$ 。如果 $pre=0$ 都未能匹配，则说明下一个位置只能从头开始。

bool flag = 0;
for (int pre = l; 1; pre = nxt[pre - 1])
{
    if (s[pre] == 'a' + m)
    {
        if (pre == sz - 1)
        {
            if (j + 1 <= k)
            {
                dp[i + 1][j + 1][0] += dp[i][j][l];
                dp[i + 1][j + 1][0] %= mod;
            }
        }
        else
        {
            dp[i + 1][j][pre + 1] += dp[i][j][l];
            dp[i + 1][j][pre + 1] %= mod;
        }
        flag = 1;
        break;
    }
    if (!pre)
        break;
}

完整代码：

void solve()
{
    int n, k;
    cin >> n >> k;
    string s;
    cin >> s;
    int sz = s.size();
    vector<int> nxt(sz);
    nxt[0] = 0;
    for (int i = 1, j = 0; i < sz; i++)
    {
        while (j && s[i] != s[j])
            j = nxt[j - 1];
        if (s[i] == s[j])
            j++;
        nxt[i] = j;
    }
    vector<vector<vector<i64>>> dp(n + 1, vector<vector<i64>>(k + 1, vector<i64>(sz + 1)));
    dp[0][0][0] = 1;
    for (int i = 0; i < n; i++)              // 前i个字符
        for (int j = 0; j <= k; j++)         // 已经匹配了j个
            for (int l = 0; l < sz; l++)     // 正在匹配第l个
                for (int m = 0; m < 26; m++) // 枚举字符
                {
                    bool flag = 0;
                    for (int pre = l; 1; pre = nxt[pre - 1])
                    {
                        if (s[pre] == 'a' + m)
                        {
                            if (pre == sz - 1)
                            {
                                if (j + 1 <= k)
                                {
                                    dp[i + 1][j + 1][0] += dp[i][j][l];
                                    dp[i + 1][j + 1][0] %= mod;
                                }
                            }
                            else
                            {
                                dp[i + 1][j][pre + 1] += dp[i][j][l];
                                dp[i + 1][j][pre + 1] %= mod;
                            }
                            flag = 1;
                            break;
                        }
                        if (!pre)
                            break;
                    }
                    if (!flag)
                    {
                        dp[i + 1][j][0] += dp[i][j][l];
                        dp[i + 1][j][0] %= mod;
                    }
                }

    i64 ans = 0;
    for (int i = 0; i < sz; i++)
    {
        ans += dp[n][k][i];
        ans %= mod;
    }
    cout << ans << endl;
}

3. 字典树Trie

写法见数据结构部分 $01$ Trie,没有本质区别。

4. Manacher马拉车算法

一种非常优秀的以线性时间复杂度求解字符串中最长回文子串的算法。

int manacher(string t)
{
    string s;
    int tot = 0;
    s.push_back('$');
    for (int i = 0; i < t.size(); i++)
    {
        s.push_back('#');
        s.push_back(t[i]);
    }
    s.push_back('#');
    int ans = 0;
    vector<int> d(s.size() + 10);
    d[0] = 1; // d[i]代表i为中心的最大半径-1,也表示原回文串长度
    for (int i = 1, l = 0, r = 0; i < s.size(); ++i)
    {
        if (i <= r)
            d[i] = min(d[l + r - i], r - i + 1);
        while (s[i + d[i]] == s[i - d[i]])
            d[i]++;
        if (d[i] + i - 1 > r)
            r = d[i] + i - 1, l = i - d[i] + 1;
        ans = max(ans, d[i]);
    }
    return ans - 1;
}

5. AC自动机

与 $KMP$ 互补，本质依旧是 $KMP$ ，实现的是多模式串 $T_1\to T_n$ 匹配唯一主串 $S$ .复杂度 $O(2\sum|T_i|+|S|)$

字典树上构建 $Fail$ 指针的思路与 $nxt$ 数组极其相似。考虑本模板中如果有 $s[i]\neq s[j]$ ，则 $j=nxt[j-1]$ 含义为 $i$ 匹配失败后所跳跃的位置。第 $i$ 个失配了，肯定要跳跃 $i-1$ 的下一个适配点，也就是 $nxt[j-1]$

考虑字典树中，如果结点 $u$ 失配，意味着结点 $u$ 的所有儿子都不适配下一个字符，但是结点 $u$ 的父亲是适配上一个字符的，所以我们要去跳转下一个对应上一个字符的结点，这个就是 $u$ 结点父亲所指向的 $Fail$ 结点。

int Fail = trie[u].fail;
for (int i = 0; i < 26; i++)
{
    int v = trie[u].son[i];
    if (!v)
    {
        trie[u].son[i] = trie[Fail].son[i];
        continue;
    }
    trie[v].fail = trie[Fail].son[i];
    in[trie[v].fail]++;
    q.push(v);
}

下面是模板，每重新一次新主串 $S$ 都要重新跳一遍 $Fail$ 指针。

版本1：（只求有多少个文本串 $T$ 于主串 $S$ 中出现过）

// 构建字典图实现自动跳转，构建失配指针实现多模式匹配。
// 本题AC自动机解决求有多少个不同的模式串在文本串里出现过，且两个模式串不同当且仅当他们编号不同；
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
struct AC
{
    const static int N = 1 * 1e6 + 4;
    int t[N][30], idx, q; // t[i][j]:表示一个节点，父节点的编号为I,自己的字符是j，idx是节点总数
    int cnt[N];           // 记录以这个点为结尾有几个单词
    int fail[N];          // 失配指针，从i跳到j就说明，word(j)是i的最长后缀！！
    int getnum(char ch)
    { // 字符转为数字
        if (ch >= 'a' && ch <= 'z')
            return ch - 'a' + 1;
    }
    void insert(string s)
    {                              // 插入
        int p = 0, len = s.size(); // 从0节点开始
        for (int i = 0; i < len; i++)
        {
            int c = getnum(s[i]);
            if (!t[p][c])
                t[p][c] = ++idx; // 创建节点
            p = t[p][c];         // 把父节点更改为上个节点
        }
        cnt[p]++; // 以该点为结尾的单词数量，因为不保证模式串一致
    }
    void build()
    {
        queue<int> q;
        memset(fail, 0, sizeof(fail));
        for (int i = 1; i <= 26; i++)
            if (t[0][i])
                q.push(t[0][i]);
        // 根节点的首字符入队
        // 不直接将0入队是为了避免指向自己
        while (!q.empty())
        {
            int k = q.front();
            q.pop(); // 当前结点
            for (int i = 1; i <= 26; i++)
            {
                if (t[k][i])
                {                                  // 如果子节点存在
                    fail[t[k][i]] = t[fail[k]][i]; // 构建当前的fail指针
                    // 原理，上一层的fail已经求出，例如上一层为her，自己是s，r的fail指向了er，若r有这个子节点s，由于er是her的最长后缀，那么ers必然是hers的最长后缀。
                    // 另外结合else的代码 ，原本按道理如果没有s这个节点应不断跳fail，但这里为什么不用呢？因为如果跳完fail的话能换到一条链，则else的代码能够帮助一步跳过去所以可以一步，如果不能，则赋值为0，同样也是根节点，完美
                    q.push(t[k][i]); // 入队
                }
                else
                    t[k][i] = t[fail[k]][i];
                // 匹配到空字符，则索引到父节点fail指针对应的字符，以供后续指针的构建
                // 类似并差集的路径压缩，把不存在的tr[k][i]全部指向tr[fail[k]][i]
                // 这句话在后面匹配主串的时候也能帮助跳转
            }
        }
    }
    int queryy(string S)
    {
        int len = S.size(), p = 0, ans = 0;
        for (int i = 0; i < len; i++)
        {
            p = t[p][getnum(S[i])];
            for (int j = p; j && ~cnt[j]; j = fail[j])
                ans += cnt[j], cnt[j] = -1; // 答案加上结尾，cnt[j]=-1就是以后别在统计这里相关的了，防止重复
            // 这个点开始跳fail数组，求得与之相关的后缀的单词有没有
            // 分析j&&~cnt[j]:只有=-1时取反才是0，所以结束条件为跳到根节点（j=0）或者到达了求过的点
            // 因为本题要求有多少个模式串出现过，所以不能重复贡献
        }
        return ans;
    }
};
AC ac;
int main()
{
    int n;
    cin >> n;
    string s;
    for (int i = 1; i <= n; i++)
    {
        cin >> s;
        ac.insert(s);
    }
    ac.build();
    cin >> s;
    cout << ac.queryy(s) << endl;
}

版本2：返回每一个 $T_i$ 的出现次数

#include <bits/stdc++.h>

using namespace std;
struct AC
{
    const static int maxn = 2e5 + 9;
    int n, cnt = 1, vis[maxn], ans, in[maxn << 5], Map[maxn];
    struct Trie
    {
        int son[26], fail, flag, ans;
        void clear() { memset(son, 0, sizeof(son)), fail = flag = ans = 0; }
    } trie[maxn << 5];
    queue<int> q;
    void init(int _n)
    {
        for (int i = 0; i <= cnt; i++)
            trie[i].clear();
        for (int i = 1; i <= n; i++)
            vis[i] = 0;
        cnt = 1;
        n = _n;
    }
    void insert(string t, int num)
    {
        int u = 1, len = t.size();
        for (int i = 0; i < len; i++)
        {
            int v = t[i] - 'a';
            if (!trie[u].son[v])
                trie[u].son[v] = ++cnt;
            u = trie[u].son[v];
        }
        if (!trie[u].flag)
            trie[u].flag = num;
        Map[num] = trie[u].flag;
    }
    void getFail()
    {
        for (int i = 0; i < 26; i++)
            trie[0].son[i] = 1;
        q.push(1);
        while (!q.empty())
        {
            int u = q.front();
            q.pop();
            int Fail = trie[u].fail;
            for (int i = 0; i < 26; i++)
            {
                int v = trie[u].son[i];
                if (!v)
                {
                    trie[u].son[i] = trie[Fail].son[i];
                    continue;
                }
                trie[v].fail = trie[Fail].son[i];
                in[trie[v].fail]++;
                q.push(v);
            }
        }
    }
    void topu()
    {
        for (int i = 1; i <= cnt; i++)
            if (in[i] == 0)
                q.push(i);
        while (!q.empty())
        {
            int u = q.front();
            q.pop();
            vis[trie[u].flag] = trie[u].ans;
            int v = trie[u].fail;
            in[v]--;
            trie[v].ans += trie[u].ans;
            if (in[v] == 0)
                q.push(v);
        }
    }
    void query(string s)
    {
        int u = 1, len = s.size();
        for (int i = 0; i < len; i++)
            u = trie[u].son[s[i] - 'a'], trie[u].ans++;
    }
    vector<int> querys(string s)
    {
        vector<int> res;
        query(s);
        topu();
        for (int i = 1; i <= n; i++)
            res.push_back(vis[Map[i]]);
        return res;
    }
};
AC ac;
int main()
{
    int n;
    cin >> n;
    ac.init(n);
    for (int i = 1; i <= n; i++)
    {
        string t;
        cin >> t;
        ac.insert(t, i);
    }
    ac.getFail();
    string s;
    cin >> s;
    auto res = ac.querys(s);
    for (auto i : res)
        cout << i << endl;
}

6. 后缀数组SA

Warning: 此处SA数组的字符串下标定义是从1开始的！

后缀数组 $sa[i]$ 表示的是字典序排名第 $i$ 小的后缀是原来字符串中哪一个后缀。

排名数组 $rk[i]$ 表示原来字符串的后缀中第 $i$ 个后缀是多少字典序。

第 $i$ 个后缀的定义： $s[i\cdots n]$

$O(nlogn)$ 求法：

struct SufArray
{
    const static int maxn = 1e6 + 9;
    // rk[i] i 的排名  sa[i] 第i名
    // 字符串的序号  +k 就是往后走k个
    int rk[maxn + 10], sa[maxn + 10], n, lstrk[maxn + 10], lstsa[maxn], w,
        m = 127, cnt[maxn], h[maxn], f[maxn][20];
    string s;

#define siz n * sizeof(int)
    void init(string _s)
    {
        s = _s;
        m = 127;
        n = s.length();
        memset(cnt, 0, sizeof cnt);
        memset(sa, 0, sizeof sa);
        memset(rk, 0, sizeof rk);
        memset(h, 0, sizeof h);
        for (int i = 1; i <= n; ++i)
            ++cnt[rk[i] = s[i - 1]];
        for (int i = 1; i <= m; ++i)
            cnt[i] += cnt[i - 1];
        for (int i = n; i >= 1; --i)
            sa[cnt[rk[i]]--] = i;
        memcpy(lstrk + 1, rk + 1, siz);
        for (int p = 0, i = 1; i <= n; ++i)
            if (lstrk[sa[i]] == lstrk[sa[i - 1]])
                rk[sa[i]] = p;
            else
                rk[sa[i]] = ++p;
        for (w = 1; w < n; w <<= 1, m = n)
        {
            for (int p = 0, i = n; i >= n - w + 1; --i)
                lstsa[++p] = i;
            for (int p = w, i = 1; i <= n; ++i)
                if (sa[i] > w)
                    lstsa[++p] = sa[i] - w;
            memset(cnt, 0, sizeof cnt);
            for (int i = 1; i <= n; ++i)
                ++cnt[rk[lstsa[i]]];
            for (int i = 1; i <= m; ++i)
                cnt[i] += cnt[i - 1];
            for (int i = n; i >= 1; --i)
                sa[cnt[rk[lstsa[i]]]--] = lstsa[i];
            memcpy(lstrk + 1, rk + 1, siz);
            for (int p = 0, i = 1; i <= n; ++i)
                if (lstrk[sa[i]] == lstrk[sa[i - 1]] && lstrk[sa[i] + w] == lstrk[sa[i - 1] + w])
                    rk[sa[i]] = p;
                else
                    rk[sa[i]] = ++p;
        }
        for (int i = 1, k = 0; i <= n; ++i)
        {
            if (rk[i] == 0)
                continue;
            if (k)
                --k;
            while (s[i + k - 1] == s[sa[rk[i] - 1] + k - 1])
                ++k;
            h[rk[i]] = k;
        }

        memset(f, 0x3f, sizeof f);
        for (int i = 1; i <= n; ++i)
            f[i][0] = h[i];
        for (int j = 1; (1 << j) <= n; ++j)
            for (int i = 1; i <= n - (1 << j) + 1; ++i)
                f[i][j] = min(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
    }
    int lcp(int x, int y)
    { // 后缀x和后缀y的最长公共前缀
        if (x == y)
            return n - y + 1;
        x = rk[x], y = rk[y];
        if (x >= y)
            swap(x, y);
        int k = log2(y - (x + 1) + 1);
        return min(f[x + 1][k], f[y - (1 << k) + 1][k]);
    }
} SA;
void solve()
{
    string s;
    cin >> s;
    SA.init(s);
    for (int i = 1; i <= SA.n; i++)
        cout << SA.sa[i] << ' ';
    cout << endl;
    // for (int i = 1; i <= SA.n; i++)
    //     cout << SA.h[i] << ' ';
    // cout << endl;
}

7. SA数组(线性SA-IS)

Warning：此处SA数组以及height数组是从0开始的

struct SA
{
    int n;
    vector<int> sa, rk;
    vector<i64> h;
    SA(string s)
    {
        n = s.size();
        s.push_back(0);
        sa.resize(n);
        h.resize(n - 1);
        rk.resize(n);
        iota(sa.begin(), sa.end(), 0);
        sort(sa.begin(), sa.end(), [&](int a, int b)
             { return s[a] < s[b]; });
        rk[sa[0]] = 0;
        for (int i = 1; i < n; ++i)
        {
            rk[sa[i]] = rk[sa[i - 1]] + (s[sa[i]] != s[sa[i - 1]]);
        }
        int k = 1;
        vector<int> tmp, cnt(n);
        tmp.reserve(n);
        while (rk[sa[n - 1]] < n - 1)
        {
            tmp.clear();
            for (int i = 0; i < k; ++i)
            {
                tmp.push_back(n - k + i);
            }
            for (auto i : sa)
            {
                if (i >= k)
                {
                    tmp.push_back(i - k);
                }
            }
            fill(cnt.begin(), cnt.end(), 0);
            for (int i = 0; i < n; ++i)
            {
                ++cnt[rk[i]];
            }
            for (int i = 1; i < n; ++i)
            {
                cnt[i] += cnt[i - 1];
            }
            for (int i = n - 1; i >= 0; --i)
            {
                sa[--cnt[rk[tmp[i]]]] = tmp[i];
            }
            swap(rk, tmp);
            rk[sa[0]] = 0;
            for (int i = 1; i < n; ++i)
            {
                rk[sa[i]] = rk[sa[i - 1]] + (tmp[sa[i - 1]] < tmp[sa[i]] || sa[i - 1] + k == n || tmp[sa[i - 1] + k] < tmp[sa[i] + k]);
            }
            k *= 2;
        }
        for (int i = 0, j = 0; i < n; ++i)
        {
            if (rk[i] == 0)
            {
                j = 0;
                continue;
            }
            for (j -= j > 0; i + j < n && sa[rk[i] - 1] + j < n && s[i + j] == s[sa[rk[i] - 1] + j];)
                ++j;
            h[rk[i] - 1] = j;
        }
    }
};

void solve()
{
    string s;
    cin >> s;
    SA sa(s);
    for (int i = 0; i < s.size(); i++)
        cout << sa.sa[i] + 1 << " ";
}

8. 后缀自动机SAM

$SAM$ 自动机是一种压缩子串信息的自动机，可以在线性时间内解决以下问题：

在另一个字符串中搜索一个字符串的所有出现位置。
计算给定的字符串中有多少个不同的子串。

struct SAM {
    //root是1
    int size, last, len[N << 1], fa[N << 1], tr[N << 1][31];
    int nxt[N << 1], head[N << 1], to[N << 1], ecnt = 1;
    int cnt[N << 1], first_pos[N << 1], is_clone[N << 1];

#define sfor(x, i) for(int i = 0; i <= 30; ++i) if(tr[x][i])
    SAM() {
        size = last = ecnt = 1;
    }
    int extend(int x) {
        int cur = ++ size,u;
        cnt[cur] = 1, first_pos[cur] = len[cur] = len[last] + 1;
        for(u = last; u && !tr[u][x]; u = fa[u]) tr[u][x] = cur;
        if(!u) fa[cur] = 1;
        else {
            int v = tr[u][x];
            if(len[v] == len[u] + 1) fa[cur] = v;
            else {
                int clone = ++ size;
                len[clone] = len[u] + 1, fa[clone] = fa[v], first_pos[clone] = first_pos[v], is_clone[clone] = 1;
                memcpy(tr[clone], tr[v], sizeof(tr[v]));//时间复杂度在这个地方
                for(; u && tr[u][x] == v; u = fa[u]) tr[u][x] = clone;
                fa[cur] = fa[v] = clone;
            }
        }
        return last = cur;
    }
    //cnt数组表示endpos的大小，默认是真实大小
    //d数组表示下面可以走多少路径，默认和endpos集合大小有关
    //每个结点的endpos集合起始就是终点结点的endpos的集合
//=========================================建树=========================================
    void add(int x, int y) {
        nxt[++ecnt] = head[x], to[ecnt] = y, head[x] = ecnt;
    }
    void build_tree() {
        for(int i = 2; i <= size; ++i) add(fa[i], i);
    }

//===========================================求occ=========================================
    int pos[N << 1], f[N << 1][20];//pos代表s[1...r]对应的结点
    //调用的时候pos[r] = extend(s[r] - 'a' + 1);
    //调用时先建树 并求得cnt
    void get_f(int x = 1){//遍历后缀链接树
        f[x][0] = fa[x];
        for(int i = 1; i <= 19; ++i) f[x][i] = f[f[x][i - 1]][i - 1];
        for(int i = head[x]; i; i = nxt[i]) if(fa[x] != to[i]) {
            get_f(to[i]);
        }
    }
    int node(int l, int r){
        int now = pos[r];
        for(int i = 19; i >= 0; --i) if(len[f[now][i]] >= r-l+1) now = f[now][i];
        return now;//找到l...r所在的结点
    }
    int occ(int l, int r){
        return cnt[node(l, r)];
    }
//==========================================求结点的cnt=======================================
    void Get_cnt(int x) {
        for(int i = head[x]; i; i = nxt[i]) Get_cnt(to[i]), cnt[x] += cnt[to[i]];
    }
    //调用时先建树
    void get_cnt(int type = 1) {
        if(type == 0) for(int i = 1; i <= size; ++i) cnt[i] = 1;    //不同位置的子串算作一个 强制每个子串只出现一次
        else Get_cnt(1);
    }
    vector<int> endpos(int x) {
        queue<int> q;
        vector<int> ep;
        q.push(x);
        while(!q.empty()) {
            int now = q.front();
            q.pop();
            if(!is_clone[now])  //是终点结点
                ep.push_back(first_pos[now]);
            for(int i = head[now]; i; i = nxt[i])
                q.push(to[i]);
        }
        return ep;
    }
    //遍历后缀树：用图那一套 从1开始 //遍历后缀自动机：从1开始用tr转移
    ll d[N], ans[N];//d记录了从x开始往下有几条路径 ans记录了从x开始，往下所有路径上不同子串的总长度。
    void get_d(int x = 1) {
        if(d[x]) return ;
        d[x] = cnt[x];
        sfor(x, i) get_d(tr[x][i]), d[x] += d[tr[x][i]];
    }
    void debug() {
        puts("--------Debug_SAM--------");
        for(int i = 1; i <= size; ++i)
            cout << "i = " << i << ", endpos_size = " << cnt[i] << ", fa = " << fa[i] << ", len = " << len[i] << ", d = " << d[i] << endl;
        for(int i = 1; i <= size; ++i) {
            cout << "i = " << i << " can trans to " << endl;
            sfor(i, j)  cout << tr[i][j] << " by " << char(j + 'a' - 1) << endl;
        }
        puts("--------End_Debug--------");
    }
} sam;

Part 6. 动态规划

1. sosdp（高维前缀和dp)

对于所有的 $i$ , $0≤i≤2^n−1$ ,求解 $∑_{j⊂i}a_j$ 。

以 $O(n2^n)$ 的复杂度管理子集前缀和 $dp$ 。

子集： $i$ 对应是 $0$ 的位置， $j$ 必须对应为 $0$

for(int j = 0; j < n; j++) 
    for(int i = 0; i < 1 << n; i++)
        if(i >> j & 1) f[i] += f[i ^ (1 << j)];

超集： $i$ 对应是 $1$ 的位置， $j$ 必须对应 $1$

for(int j = 0; j < n; j++) 
    for(int i = 0; i < 1 << n; i++)
        if(!(i >> j & 1)) f[i] += f[i ^ (1 << j)];

示例1：（2024湖南省赛）

给出一个长度为 $n$ 的正整数串。现在可以把两个没有重叠的连续子串前后拼接起来，但是要求拼接之后的数串中每个正整数不能出现超过 $1$ 次。请问能拼接出来的符合要求的数字串的最大长度是多少。保证 $a_i\le18$ .

数据范围一眼状压 $dp$ ，考虑维护出现不超过一次。显然两个串的 $mask$ 位的交集为 $0$ ，考虑串 $A$ 的 $mask$ 位 $K$ ，则显然串 $B$ 的 $mask$ 必定有 $mask_B\subset(2^{18}\oplus mask_A)$

串长度不超过 $18$ ，暴力枚举所有合法串初始化 $dp$ 数组，然后跑 $sosdp$ 维护子集 $max$ ，最后暴力检查一圈就行了。

#include <bits/stdc++.h>
using namespace std;
const int B = (1 << 18) - 1;
int mp[2 * B];
signed main()
{
    int n;
    cin >> n;
    vector<int> a(n + 1);
    for (int i = 1; i <= n; i++)
        cin >> a[i], a[i]--;
    int i = 1, j = 1;
    int bit = 0;
    for (int i = 1; i <= n; i++)
    {
        bit = 0;
        for (int j = 0; j < 18 && j + i <= n; j++)
        {
            if ((bit >> a[i + j]) & 1)
            {
                break;
            }
            bit ^= (1 << a[i + j]);
            mp[bit] = max(mp[bit], j + 1);
        }
    }
    int ans = 0;
    for (int j = 0; j < 18; j++)
    {
        for (int i = 0; i <= B; i++)
        {
            if (i >> j & 1)
                mp[i] = max(mp[i], mp[i ^ (1 << j)]);
        }
    }
    for (int i = 0; i <= B; i++)
    {
        ans = max(ans, mp[i] + mp[B ^ i]);
    }
    cout << ans << endl;
}

2.线性dp

2.1 LIS ( $O(nlogn)$ )

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
const int inf = 0x3f3f3f3f;
int a[N], dp[N], dp2[N];
int main()
{
    int n, ans = 0;
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        dp[i] = 1;
    }
    // O(nlogn)做法
    int maxx = 0;
    memset(dp2, inf, sizeof(dp2));
    for (int i = 1; i <= n; i++)
    {
        int j = lower_bound(dp2, dp2 + n, a[i]) - dp2;
        if (j + 1 > maxx)
            maxx = j + 1;
        dp2[j] = a[i];
    }
    cout << maxx << endl;
}

单调栈优化：

int arr[maxn], sta[maxn];
signed main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> arr[i];
    int len = 1;
    sta[len] = arr[1];
    for (int i = 2; i <= n; i++)
    {
        if (arr[i] > sta[len])
        {
            sta[++len] = arr[i];
        }
        else
        {
            int tem = lower_bound(sta + 1, sta + 1 + len, arr[i]) - sta;
            sta[tem] = arr[i];
        }
    }
    cout << len << endl;
    // system("pause");
    return 0;
}

2.2 背包

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 2;
// 物品容积与权重
int c[N], w[N], dp[N];
int main()
{
    // 01背包
    // 物品数目与背包体积
    int n, v;
    for (int i = 1; i <= n; i++)        // 枚举所有物品
        for (int j = v; j >= c[i]; j--) // 枚举背包体积
            dp[j] = max(dp[j], dp[j - c[i]] + w[i]);
    // 分组背包
    // t[k][i]表示第k组的第i件物品的编号是多少
    int ts, m, cnt[N], t[N][N];
    for (int k = 1; k <= ts; k++)                                        // 循环每一组
        for (int i = m; i >= 0; i--)                                     // 循环背包容量
            for (int j = 1; j <= cnt[k]; j++)                            // 循环该组的每一个物品
                if (i >= w[t[k][j]])                                     // 背包容量充足
                    dp[i] = max(dp[i], dp[i - w[t[k][j]]] + c[t[k][j]]); // 像0 - 1背包一样状态转移
}

2.3 整数划分

ll dp[maxn][maxn];
ll f[maxn][maxn], g[maxn][maxn];
int n, k;
void div1()
{
    // dp[i][j] 代表将i划分为不大于j的划分数(允许重复数字)
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= k; j++)
        {
            if (j == 1)
                dp[i][j] = 1;
            else if (i == j)
                dp[i][j] = dp[i][j - 1] + 1;
            else if (i < j)
                dp[i][j] = dp[i][i];
            else
                dp[i][j] = dp[i][j - 1] + dp[i - j][j];
        }
    }
}
void div2()
{
    // dp[i][j] 代表将i划分为不大于j的划分数(没有重复数字)
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= k; j++)
        {
            if (j == 1)
            {
                if (i == 1)
                    dp[i][j] = 1;
                else
                    dp[i][j] = 0; // 初始化不同即可, 转移方程依旧相同.
            }
            else if (i == j)
                dp[i][j] = dp[i][j - 1] + 1;
            else if (i < j)
                dp[i][j] = dp[i][i];
            else
                dp[i][j] = dp[i][j - 1] + dp[i - j][j - 1];
        }
    }
}
void div3()
{
    // dp[i][j]为将i恰好划分为j个整数的划分数
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= k; j++)
        {
            if (i == j)
                dp[i][j] = 1;
            else if (i < j)
                dp[i][j] = 0;
            else
                dp[i][j] = dp[i - 1][j - 1] + dp[i - j][j];
        }
    }
}
void div4()
{
    // 设f[i][j]为将i恰好划分为j个奇数之和的划分数
    //  g[i][j]为将i恰好划分为j个偶数之和的划分数。
    f[0][0] = g[0][0] = 1;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= k; j++)
        {
            if (i < j)
                f[i][j] = g[i][j] = 0;
            else
            {
                f[i][j] = f[i - 1][j - 1] + g[i - j][j];
                g[i][j] = f[i - j][j];
            }
        }
    }
}
void div5()
{
    // dp[i][j] 代表i划分为不多于j个正整数的划分数
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= k; j++)
        {
            if (i == 1 || j == 1)
                dp[i][j] = 1;
            else if (i == j)
                dp[i][j] = dp[i][j - 1] + 1;
            else if (i < j)
                dp[i][j] = dp[i][i];
            else
                dp[i][j] = dp[i][j - 1] + dp[i - j][j];
        }
    }
}

2.4 数位dp

int a[maxn], f[maxn][maxn][2];
// f[len][state],状压的state记录状态
int dfs(int pos, int pre, bool limit, bool lead0, int cnt) {
    if (!pos)
        return 1;  // 看情况return 1还是cnt
    auto& now = f[pos][pre][limit];
    if (!lead0 && ~now)
        return now;
    int up = limit ? a[pos] : 9;
    int res = 0;
    for (int i = 0; i <= up; i++) {
        if (!lead0 && abs(i - pre) < 2)
            continue;  // 保证枚举的要合法
        res += dfs(pos - 1, i, limit && i == up, lead0 && i == 0, cnt);
    }
    if (!lead0)
        now = res;
    return res;
}
int solve(int x) {
    int len = 0;
    while (x > 0) {
        a[++len] = x % 10;
        x /= 10;
    }
    return dfs(len, 0, true, true, 0);
}

2.5 四边形不等式优化dp

int m[maxn][maxn],dp[maxn][maxn],sum[maxn],arr[maxn];
//m是区间分割点
signed main(){
    int n;cin>>n;
    for(int i=1;i<=n;i++){
        cin>>arr[i];
        sum[i]=sum[i-1]+arr[i];
        m[i][i]=i;
    }
    for(int len=2;len<=n;len++){//枚举区间长度，也是对角线条数
        for(int i=1,j=len;j<=n;i++,j++){
            dp[i][j]=inf;
            for(int k=m[i][j-1];k<=m[i+1][j];k++){
                if(dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1]<dp[i][j]){
                    dp[i][j]=dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1];
                    m[i][j]=k;
                }
            }
        }
    }
    cout<<dp[1][n]<<endl;
}

2.6 状态压缩dp

using namespace std;
const int maxn = 1 << 16;
db f[17][1 << 17]; // 当前到第i个奶酪，并且已经经过的状态为j
db d[17][17];
db x[17] = {0}, y[17] = {0};
db dis(int i, int j)
{
    return sqrt((x[i] - x[j]) * (x[i] - x[j]) + (y[i] - y[j]) * (y[i] - y[j]));
}
int main()
{
    int n = read();
    memset(f, 127, sizeof(f));
    db ans = f[0][0];
    for (int i = 1; i <= n; i++)
        cin >> x[i] >> y[i];
    for (int i = 0; i <= n; i++)
        for (int j = i + 1; j <= n; j++)
            d[i][j] = d[j][i] = dis(i, j); // 初始化任意两个奶酪之间的距离
    for (int i = 1; i <= n; i++)
        f[i][1 << (i - 1)] = d[0][i];
    for (int j = 0; j < (1 << n); j++)
    { // 枚举当前已经走过的状态
        for (int i = 1; i <= n; i++)
        {								   // 枚举当前已经到第i个奶酪
            if ((j & (1 << (i - 1))) == 0) // 本应已经到了i个奶酪，但是还没走过i不合题意
                continue;
            for (int k = 1; k <= n; k++)
            { // 枚举上一个走到的奶酪
                if (i == k)
                    continue;				   // 重复了跳过
                if ((j & (1 << (k - 1))) == 0) // 目前走过的j没走过k
                    continue;
                f[i][j] = min(f[i][j], f[k][j - (1 << (i - 1))] + d[i][k]);
            }
        }
    }
    for (int i = 1; i <= n; i++)
        ans = min(ans, f[i][(1 << n) - 1]);
    cout << fixed << setprecision(2) << ans << endl;
    return 0;
}

2.7 最短路优化dp

最短路 $dp$ 后效性问题会被最短路优化掉。

#include <bits/stdc++.h>
using namespace std;
int n, m;
#define int long long
const int maxn = 2e5 + 9;
vector<pair<int, int>> connects[maxn];
int a[maxn];
void add_edge(int u, int v, int w)
{
    connects[u].push_back({v, w});
    connects[v].push_back({u, w});
    return;
}
vector<int> dist, dist1;
void Dijkstra_queue0()
{
    using pi = pair<int, int>;
    vector<bool> vis(n + 1, 0);
    priority_queue<pi, vector<pi>, greater<pi>> q;
    for (int i = 1; i <= n; i++)
    {
        q.push({dist[i], i});
    }
    while (!q.empty())
    {
        auto [dis, u] = q.top();
        q.pop();
        if (vis[u])
            continue;
        vis[u] = 1;
        for (auto [v, w] : connects[u])
        {
            if (vis[v])
                continue;
            if (dist[v] > dist[u] + w)
            {
                dist[v] = dist[u] + w;
                q.push({dist[v], v});
            }
        }
    }
    return;
}
void Dijkstra_queue1()
{
    using pi = pair<int, int>;
    vector<bool> vis(n + 1, 0);
    priority_queue<pi, vector<pi>, greater<pi>> q;
    for (int i = 1; i <= n; i++)
    {
        q.push({dist1[i], i});
    }
    while (!q.empty())
    {
        auto [dis, u] = q.top();
        q.pop();
        if (vis[u])
            continue;
        vis[u] = 1;
        for (auto [v, w] : connects[u])
        {
            int now = min(dist[u], dist1[u] + w);
            if (now < dist1[v])
            {
                dist1[v] = now;
                q.push({dist1[v], v});
            }
        }
    }
    return;
}
signed main()
{
    cin >> n >> m;
    for (int i = 1; i <= m; i++)
    {
        int u, v, w;
        cin >> u >> v >> w;
        add_edge(u, v, w);
    }
    dist.resize(n + 10), dist1.resize(n + 10);
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        dist[i] = dist1[i] = a[i];
    }
    Dijkstra_queue0();
    Dijkstra_queue1();
    cout << *max_element(dist1.begin() + 1, dist1.end()) << endl;
}